Is 3/4 More Than 2/3
saludintensiva
Sep 16, 2025 · 5 min read
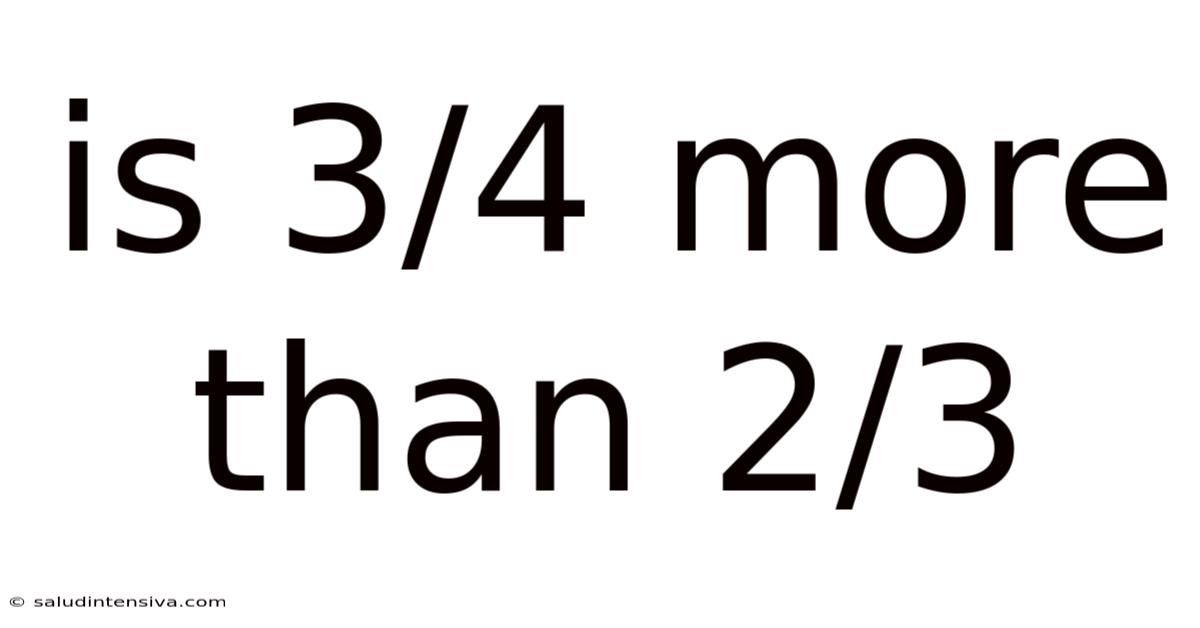
Table of Contents
Is 3/4 More Than 2/3? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, essential for everyday life and advanced studies. This article will comprehensively explore the question: "Is 3/4 more than 2/3?" We'll delve into various methods for comparing fractions, providing a clear and detailed explanation accessible to all levels of understanding. We'll also address common misconceptions and provide practical examples to solidify your grasp of this concept.
Introduction: Understanding Fractions
Before comparing 3/4 and 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator is 3 and the denominator is 4. This means we have 3 out of 4 equal parts of a whole.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means converting both fractions so they have the same denominator. Once they share a denominator, we can directly compare their numerators.
To find a common denominator for 3/4 and 2/3, we need to find the least common multiple (LCM) of 4 and 3. The multiples of 4 are 4, 8, 12, 16… and the multiples of 3 are 3, 6, 9, 12, 15… The least common multiple is 12.
Now, we convert both fractions to have a denominator of 12:
-
3/4: To change the denominator from 4 to 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
-
2/3: To change the denominator from 3 to 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
Now we can easily compare: 9/12 is greater than 8/12. Therefore, 3/4 is greater than 2/3.
Method 2: Converting to Decimals
Another method for comparing fractions is to convert them into decimals. This involves dividing the numerator by the denominator.
-
3/4: 3 ÷ 4 = 0.75
-
2/3: 2 ÷ 3 = 0.666... (a repeating decimal)
Comparing the decimal values, 0.75 is clearly greater than 0.666... Again, we conclude that 3/4 is greater than 2/3.
Method 3: Visual Representation
A visual approach can be helpful, especially for beginners. Imagine two identical circles.
-
Divide the first circle into four equal parts and shade three of them (representing 3/4).
-
Divide the second circle into three equal parts and shade two of them (representing 2/3).
By visually comparing the shaded areas, it's evident that the shaded portion of the first circle (3/4) is larger than the shaded portion of the second circle (2/3). This confirms that 3/4 is greater than 2/3.
Method 4: Cross-Multiplication
This method provides a quick way to compare fractions without finding a common denominator. We cross-multiply the numerators and denominators:
-
Multiply the numerator of the first fraction (3) by the denominator of the second fraction (3): 3 x 3 = 9
-
Multiply the numerator of the second fraction (2) by the denominator of the first fraction (4): 2 x 4 = 8
Since 9 > 8, we conclude that 3/4 is greater than 2/3.
The Significance of Understanding Fraction Comparison
The ability to compare fractions is crucial for various reasons:
-
Everyday Life: From cooking (measuring ingredients) to budgeting (managing finances), comparing fractions is a practical skill.
-
Academic Success: A solid understanding of fractions is fundamental for success in mathematics, science, and other STEM fields.
-
Problem-Solving: Comparing fractions is a core component of problem-solving in many real-world situations.
Common Misconceptions about Fraction Comparison
-
Comparing Numerators Only: Many students mistakenly compare only the numerators, assuming the larger numerator always indicates a larger fraction. This is incorrect; the denominator plays a crucial role.
-
Comparing Denominators Only: Similarly, focusing solely on the denominators is also wrong. A smaller denominator doesn't automatically mean a larger fraction.
-
Ignoring the Whole: Remember that fractions represent parts of a whole. Ensure both fractions refer to the same whole before comparing them.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to compare fractions? A: Yes, you can convert fractions to decimals using a calculator and then compare the decimal values. However, understanding the underlying methods is crucial for developing a strong mathematical foundation.
-
Q: Are there other methods for comparing fractions besides those mentioned? A: While the methods discussed are the most common and effective, other approaches exist, depending on the complexity of the fractions involved.
-
Q: What if the fractions are mixed numbers (containing a whole number and a fraction)? A: Convert the mixed numbers into improper fractions (where the numerator is larger than the denominator) before applying any of the comparison methods.
-
Q: How can I improve my understanding of fractions? A: Practice is key! Work through various examples, using different comparison methods. Visual aids and interactive online resources can also be beneficial.
Conclusion: Mastering Fraction Comparison
This detailed exploration demonstrates conclusively that 3/4 is greater than 2/3. We've explored multiple methods for comparing fractions, highlighting their strengths and clarifying common misconceptions. By understanding and practicing these techniques, you'll build a strong foundation in fraction comparison, a skill essential for success in mathematics and beyond. Remember, the key is to choose the method that feels most comfortable and effective for you, and practice regularly to solidify your understanding. Mastering fractions isn't just about getting the right answer; it's about developing a deeper understanding of numerical relationships and problem-solving strategies.
Latest Posts
Latest Posts
-
How To Subtract With Regrouping
Sep 16, 2025
-
5to The Power Of 4
Sep 16, 2025
-
8 3 As A Percentage
Sep 16, 2025
-
Fahrenheit Is What In Celsius
Sep 16, 2025
-
25 8 As A Mixed Number
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 More Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.