8 3 As A Percentage
saludintensiva
Sep 16, 2025 · 5 min read
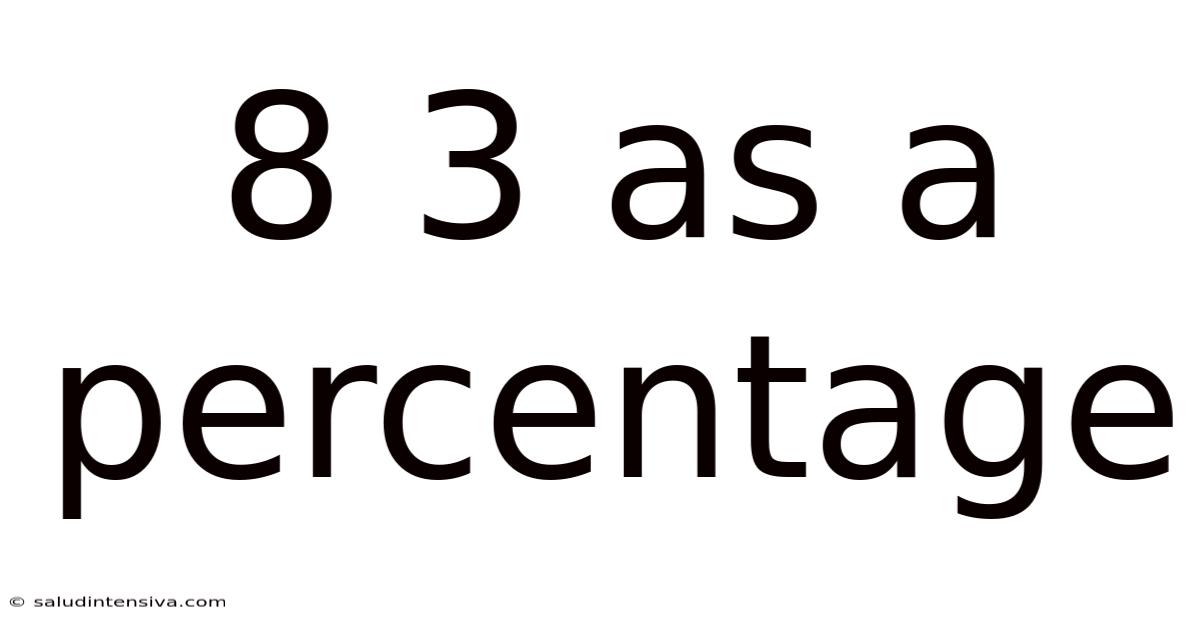
Table of Contents
Understanding 8/3 as a Percentage: A Comprehensive Guide
Expressing fractions as percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday life. This comprehensive guide delves into the intricacies of converting the fraction 8/3 into a percentage, providing not just the answer but a thorough understanding of the underlying concepts and methods. We'll explore different approaches, address common misconceptions, and offer practical examples to solidify your understanding. This guide is designed for learners of all levels, from beginners grappling with basic percentage calculations to those seeking a deeper understanding of fractional representations.
Understanding Fractions and Percentages
Before we tackle the conversion of 8/3, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 8/3, 8 is the numerator and 3 is the denominator. This means we have 8 parts out of a total of 3 parts. This might seem counterintuitive initially, because it's an improper fraction (the numerator is larger than the denominator), indicating a quantity greater than one whole.
A percentage, on the other hand, expresses a fraction as a portion of 100. The symbol "%" signifies "per hundred". Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. The core idea is to express a proportion relative to a standard base of 100.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is perhaps the most straightforward method. We first convert the improper fraction 8/3 into a decimal, and then convert that decimal into a percentage.
-
Divide the Numerator by the Denominator: Divide 8 by 3. This gives us 2.666666... (a repeating decimal).
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
2.666666... x 100 = 266.6666...%
Therefore, 8/3 as a percentage is approximately 266.67%. The slight rounding is acceptable in most contexts, but it's crucial to understand that the decimal part is repeating infinitely.
Method 2: Understanding the Whole and the Remainder
Since 8/3 is an improper fraction, we can visualize it as containing whole numbers and a remaining fraction.
-
Find the Whole Number: How many times does 3 go into 8? It goes in 2 times (3 x 2 = 6).
-
Find the Remainder: Subtract the whole number's product (6) from the numerator (8): 8 - 6 = 2.
-
Express as a Mixed Number: This gives us a mixed number: 2 and 2/3.
-
Convert the Fractional Part to a Percentage: Now we convert the fractional part (2/3) to a percentage. Dividing 2 by 3 gives approximately 0.666666..., which multiplied by 100 gives approximately 66.67%.
-
Combine the Whole Number and Percentage: We have 2 whole units (representing 200%) plus 66.67%, resulting in approximately 266.67%.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. We set up a proportion where x represents the percentage we're looking for:
8/3 = x/100
To solve for x, we cross-multiply:
3x = 800
x = 800/3
x ≈ 266.67
Therefore, 8/3 is approximately 266.67%.
The Significance of the Repeating Decimal
It's important to note the repeating decimal (0.6666...) resulting from 2/3. This is a rational number, meaning it can be expressed as a fraction, but its decimal representation is non-terminating. When rounding, we need to be aware that we're introducing a small amount of error. For most practical purposes, rounding to 266.67% is sufficient, but in scientific or engineering calculations, you might need to retain more decimal places or use the exact fractional representation.
Practical Applications and Examples
Understanding the conversion of fractions to percentages is vital in many situations:
-
Finance: Calculating interest rates, profit margins, and discounts often involves converting fractions to percentages. For instance, if a company's profit is 8/3 times its investment, this represents a huge profit margin of approximately 266.67%.
-
Statistics: Presenting data in percentage form makes it easier to understand and compare. If 8 out of 3 surveyed people prefer a certain product, this translates to about 266.67% preference (though this would typically be presented differently, considering that this indicates a flawed survey design).
-
Everyday Calculations: Determining sales tax, calculating tips, or understanding discounts all involve percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: Why is 8/3 greater than 100%? A: Because 8/3 is an improper fraction, it represents more than one whole unit. It's 2 and 2/3, which means it's more than 100% (representing one whole).
-
Q: Can I use a calculator to convert 8/3 to a percentage? A: Yes, most calculators can perform this conversion easily. Simply divide 8 by 3, then multiply the result by 100.
-
Q: What if I need a more precise answer than 266.67%? A: You can express the answer as a mixed number (2 2/3) or as a repeating decimal (266.666...). The level of precision needed depends on the context of the problem.
Conclusion
Converting 8/3 to a percentage demonstrates the essential connection between fractions and percentages. This seemingly simple conversion highlights the importance of understanding fractions, decimals, and their interconnectedness. Through the various methods outlined, we’ve not only arrived at the answer (approximately 266.67%) but also developed a deeper comprehension of the mathematical principles involved. Remember to choose the method that best suits your understanding and the level of precision required for your specific application. Mastering this concept is a stepping stone to more advanced mathematical concepts and problem-solving skills.
Latest Posts
Latest Posts
-
1 4 As A Mixed Number
Sep 16, 2025
-
Multiplying And Dividing Rational Calculator
Sep 16, 2025
-
Ft 2 To In 2
Sep 16, 2025
-
4 8 Is Equal To
Sep 16, 2025
-
Convert 43 Fahrenheit To Celsius
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 8 3 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.