1/4 As A Mixed Number
saludintensiva
Sep 16, 2025 · 6 min read
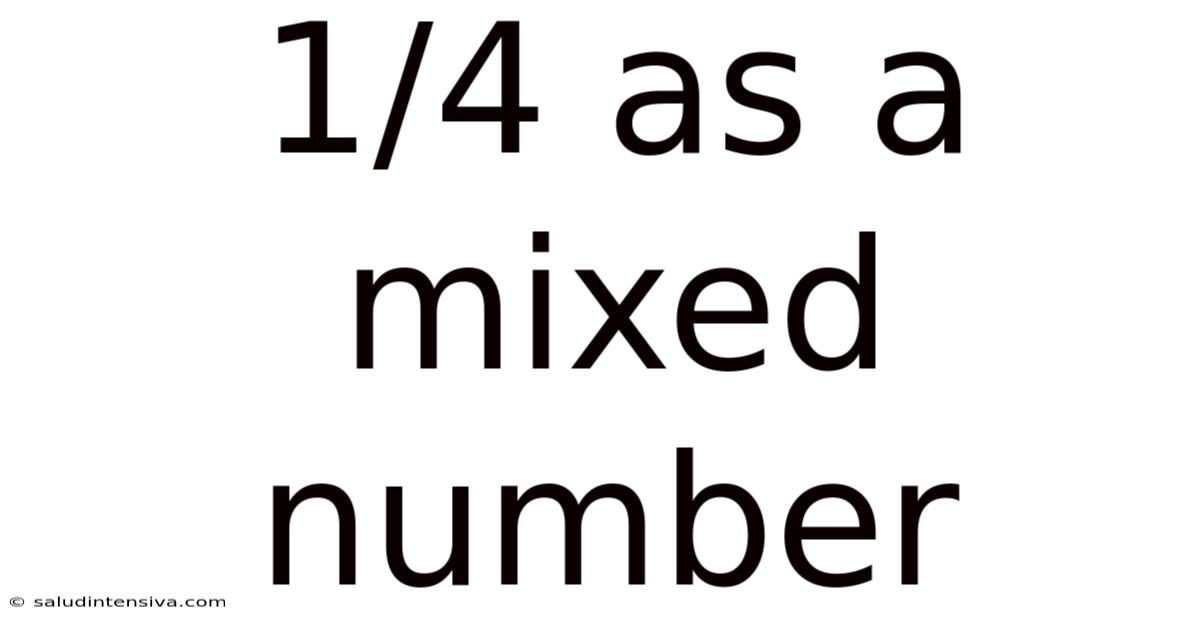
Table of Contents
Understanding 1/4 as a Mixed Number: A Comprehensive Guide
Fractions are fundamental building blocks in mathematics, forming the basis for more complex concepts. Understanding how to represent fractions in different forms is crucial for success in various mathematical applications. This article delves into the concept of expressing the fraction 1/4 as a mixed number, explaining the process step-by-step, providing examples, exploring the underlying mathematical principles, and answering frequently asked questions. This comprehensive guide aims to solidify your understanding of fractions and their representation, empowering you to tackle more advanced mathematical challenges.
What is a Mixed Number?
Before we dive into converting 1/4, let's clarify what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For instance, 1 ½, 3 ¾, and 2 ⅕ are all examples of mixed numbers. They represent a quantity that is greater than one whole unit.
Why Convert Fractions to Mixed Numbers?
Converting fractions to mixed numbers, and vice-versa, is a valuable skill with practical applications. It offers a more intuitive way to understand quantities larger than one. Imagine you have 7/4 pizzas. While 7/4 is accurate, it's not as immediately clear as saying you have 1 ¾ pizzas. Mixed numbers make it easier to visualize and compare quantities, particularly in real-world scenarios involving measurements, quantities, or sharing.
Converting 1/4 to a Mixed Number: A Step-by-Step Guide
Now, let's focus on converting 1/4 to a mixed number. The process is straightforward because 1/4 is already a proper fraction. It represents a quantity less than one whole. Therefore, 1/4 cannot be expressed as a mixed number. It remains simply as 1/4.
To illustrate the process more generally, let's consider a fraction that can be converted into a mixed number, such as 7/4. Here's how we do it:
-
Division: Divide the numerator (7) by the denominator (4). 7 ÷ 4 = 1 with a remainder of 3.
-
Whole Number: The quotient (1) becomes the whole number part of the mixed number.
-
Fraction: The remainder (3) becomes the numerator of the fraction, and the denominator remains the same (4). This gives us the fraction 3/4.
-
Mixed Number: Combine the whole number and the fraction to form the mixed number: 1 ¾.
Therefore, 7/4 is equivalent to 1 ¾.
Understanding the Mathematical Principles
The conversion from an improper fraction (where the numerator is greater than or equal to the denominator) to a mixed number relies on the fundamental concept of dividing the whole into parts. When we divide 7 by 4, we're essentially asking how many groups of 4 we can make from 7. We can make one complete group of 4, leaving 3 remaining. This remaining 3, still out of the original 4 parts, forms the fractional component of the mixed number.
Examples of Converting Improper Fractions to Mixed Numbers
Let's solidify our understanding with more examples:
- 11/5: 11 ÷ 5 = 2 with a remainder of 1. Therefore, 11/5 = 2 1/5.
- 17/6: 17 ÷ 6 = 2 with a remainder of 5. Therefore, 17/6 = 2 5/6.
- 23/8: 23 ÷ 8 = 2 with a remainder of 7. Therefore, 23/8 = 2 7/8.
- 9/2: 9 ÷ 2 = 4 with a remainder of 1. Therefore, 9/2 = 4 1/2.
These examples demonstrate the consistent application of the division method to convert improper fractions into their mixed number equivalents.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. This is achieved as follows:
- Multiplication: Multiply the whole number by the denominator of the fraction.
- Addition: Add the result to the numerator of the fraction.
- Improper Fraction: This sum becomes the numerator of the improper fraction, while the denominator remains the same.
Let's use the example of 2 3/4:
- 2 * 4 = 8
- 8 + 3 = 11
- The improper fraction is 11/4.
Real-World Applications of Mixed Numbers
Mixed numbers are ubiquitous in everyday life. Consider these examples:
- Cooking: A recipe might call for 2 ½ cups of flour.
- Measurement: The length of a piece of wood could be 3 1/8 feet.
- Time: A race might last 1 ¼ hours.
- Construction: A project might require 5 2/3 gallons of paint.
In each of these instances, the use of mixed numbers provides a clear and practical representation of the quantities involved. They facilitate easier understanding and calculation compared to using solely improper fractions.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to mixed numbers?
A: No. Only improper fractions (where the numerator is greater than or equal to the denominator) can be converted into mixed numbers. Proper fractions (where the numerator is less than the denominator), such as 1/4, cannot be expressed as mixed numbers.
Q: What if the remainder is zero after division?
A: If the remainder is zero, it means the fraction is already a whole number. For example, 8/4 = 2, a whole number. There is no fractional part to the mixed number.
Q: Is there more than one way to represent the same quantity using mixed numbers?
A: No. A given quantity can only be expressed as one specific mixed number in its simplest form. For example, 1 ¾ is unique and cannot be represented differently as a mixed number. However, you could express it as an improper fraction (7/4) or as a decimal (1.75).
Q: Why is it important to learn about mixed numbers?
A: Mastering the conversion between fractions and mixed numbers is essential for solving various mathematical problems and understanding real-world applications. It builds a strong foundation for further mathematical studies involving fractions, decimals, and percentages.
Conclusion
Understanding how to work with fractions and mixed numbers is a crucial skill that underpins a vast range of mathematical concepts and real-world applications. This article has provided a comprehensive guide to understanding 1/4 (which remains as 1/4 as it's a proper fraction) and how to convert improper fractions to mixed numbers and vice-versa. The step-by-step procedures, examples, and frequently asked questions section have aimed to solidify your understanding and empower you to confidently tackle various mathematical problems involving fractions and mixed numbers with greater ease and comprehension. Remember, consistent practice is key to mastering these fundamental concepts and building a strong foundation for future mathematical learning.
Latest Posts
Latest Posts
-
8 7 8 As A Decimal
Sep 16, 2025
-
What Are Multiples Of 20
Sep 16, 2025
-
1 10 000 As A Decimal
Sep 16, 2025
-
6 8 Is Equal To
Sep 16, 2025
-
Area Of A Pipe Formula
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1/4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.