1/2 + 1/5 In Fraction
saludintensiva
Sep 16, 2025 · 6 min read
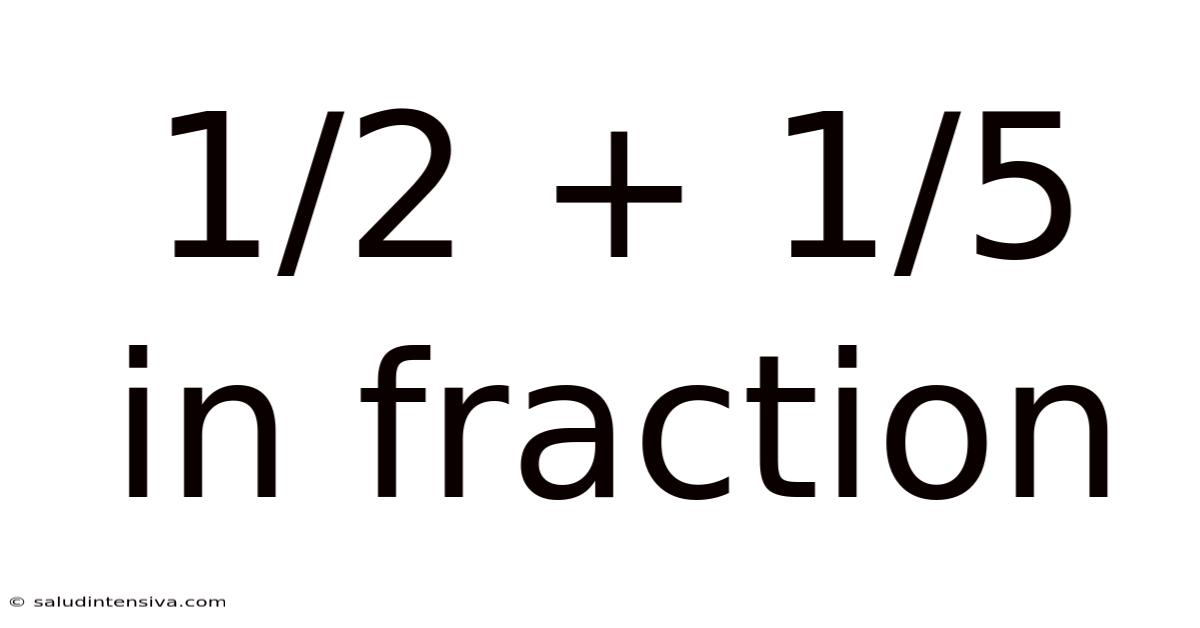
Table of Contents
Mastering Fractions: A Deep Dive into Adding 1/2 and 1/5
Adding fractions might seem daunting at first, especially when the denominators (the bottom numbers) are different. This comprehensive guide will walk you through adding 1/2 and 1/5, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common questions. By the end, you'll not only know the answer but also understand the why behind the method, empowering you to tackle any fraction addition problem with confidence. This guide covers the fundamental concepts of fractions, the importance of finding a common denominator, and provides practical examples and tips for solving similar problems.
Introduction to Fractions
Before we dive into adding 1/2 and 1/5, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the top number) and 'b' is the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have.
For example, in the fraction 1/2, the denominator 2 tells us the whole is divided into two equal parts, and the numerator 1 tells us we have one of those parts. Similarly, in 1/5, the whole is divided into five equal parts, and we have one of them.
Why We Need a Common Denominator
Adding fractions with different denominators isn't as simple as adding the numerators and the denominators directly. Imagine trying to add apples and oranges – you can't just add them together and call it "apploranges". Similarly, you can't directly add 1/2 and 1/5 until they represent parts of the same whole. That's where the concept of a common denominator comes in.
A common denominator is a number that is a multiple of both denominators. In simpler terms, it's a number that both denominators can divide into evenly. Finding a common denominator allows us to express both fractions in terms of the same-sized pieces, making addition possible.
Finding the Least Common Denominator (LCD)
While any common denominator will work, it's most efficient to use the least common denominator (LCD). The LCD is the smallest number that is a multiple of both denominators. There are several ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find a common one. For 2 and 5:
- Multiples of 2: 2, 4, 6, 8, 10, 12...
- Multiples of 5: 5, 10, 15, 20... The smallest common multiple is 10.
-
Prime Factorization: Break down each denominator into its prime factors. The LCD is the product of the highest powers of all prime factors present in either denominator.
- 2 = 2
- 5 = 5 The LCD is 2 x 5 = 10
Adding 1/2 and 1/5: A Step-by-Step Guide
Now that we understand the concept of a common denominator, let's add 1/2 and 1/5:
-
Find the LCD: As we determined earlier, the LCD of 2 and 5 is 10.
-
Convert Fractions to Equivalent Fractions: We need to rewrite both fractions with a denominator of 10. To do this, we multiply the numerator and denominator of each fraction by the number that makes the denominator equal to 10.
- For 1/2, we multiply both the numerator and denominator by 5: (1 x 5) / (2 x 5) = 5/10
- For 1/5, we multiply both the numerator and denominator by 2: (1 x 2) / (5 x 2) = 2/10
-
Add the Numerators: Now that both fractions have the same denominator, we can add the numerators: 5/10 + 2/10 = (5 + 2) / 10 = 7/10
-
Simplify (if necessary): In this case, 7/10 is already in its simplest form because 7 and 10 share no common factors other than 1.
Therefore, 1/2 + 1/5 = 7/10
Visual Representation
Imagine you have a pizza cut into 10 slices. 1/2 of the pizza is 5 slices (5/10), and 1/5 of the pizza is 2 slices (2/10). If you combine those, you have 7 slices out of 10, which is 7/10 of the pizza.
Explanation with Mathematical Properties
The process of adding fractions relies on several key mathematical properties:
-
Equivalence: Fractions like 1/2 and 5/10 are equivalent because they represent the same quantity. Multiplying or dividing both the numerator and denominator by the same non-zero number doesn't change the value of the fraction.
-
Distributive Property: When we convert fractions to a common denominator, we're essentially using the distributive property of multiplication over addition. For example, when we convert 1/2 to 5/10, we're multiplying both the numerator and denominator by 5, which is equivalent to multiplying the entire fraction by 5/5 (which equals 1, and thus doesn't change the value).
-
Addition of Fractions with Common Denominators: Adding fractions with the same denominator involves simply adding the numerators and keeping the denominator the same. This is because we're adding the same type of units (tenths, in this case).
Addressing Common Mistakes
-
Adding Numerators and Denominators Directly: A common mistake is to add the numerators and denominators separately (e.g., 1/2 + 1/5 = 2/7). This is incorrect; you must find a common denominator first.
-
Incorrectly Converting Fractions: Carefully multiply both the numerator and denominator by the same number when converting to a common denominator. Forgetting to multiply the numerator will lead to an incorrect result.
-
Not Simplifying the Result: Always simplify the final answer to its lowest terms by dividing the numerator and denominator by their greatest common divisor.
Frequently Asked Questions (FAQ)
Q: What if the denominators have a larger common factor?
A: The process remains the same. Find the LCD using the methods described above, and then convert the fractions accordingly. The more practice you get, the quicker you'll become at identifying the LCD.
Q: Can I add more than two fractions?
A: Yes, the process extends to adding any number of fractions. Find the LCD of all the denominators, convert all fractions to that denominator, and then add the numerators.
Q: What if the resulting fraction is an improper fraction (where the numerator is greater than the denominator)?
A: You can convert the improper fraction to a mixed number. For example, if you end up with 17/10, you can convert it to 1 7/10.
Q: Are there any shortcuts for finding the LCD?
A: For simple denominators, you can often find the LCD by inspection. For more complex cases, using prime factorization or the least common multiple (LCM) method is more reliable.
Q: How can I improve my skills in working with fractions?
A: Practice is key. Work through various fraction addition problems, gradually increasing the difficulty. Use visual aids like diagrams to help understand the concepts.
Conclusion
Adding fractions, even those with different denominators, becomes a manageable task with a systematic approach. By understanding the concept of a common denominator, following the steps outlined above, and practicing regularly, you can confidently solve any fraction addition problem, no matter the complexity. Remember the key steps: find the LCD, convert fractions, add numerators, and simplify the result. Mastering fractions is a fundamental skill in mathematics, and with consistent effort, you'll gain the confidence and proficiency to excel in your mathematical endeavors. Don't be afraid to make mistakes – they're a valuable part of the learning process. Keep practicing, and you'll master the art of fraction addition in no time!
Latest Posts
Latest Posts
-
22 Percent As A Fraction
Sep 16, 2025
-
3 4 X 1 6
Sep 16, 2025
-
Simplest Form Of 12 15
Sep 16, 2025
-
What Is 2 5 2 3
Sep 16, 2025
-
18 000 Minutes To Hours
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1/2 + 1/5 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.