3 4 X 1 6
saludintensiva
Sep 16, 2025 · 5 min read
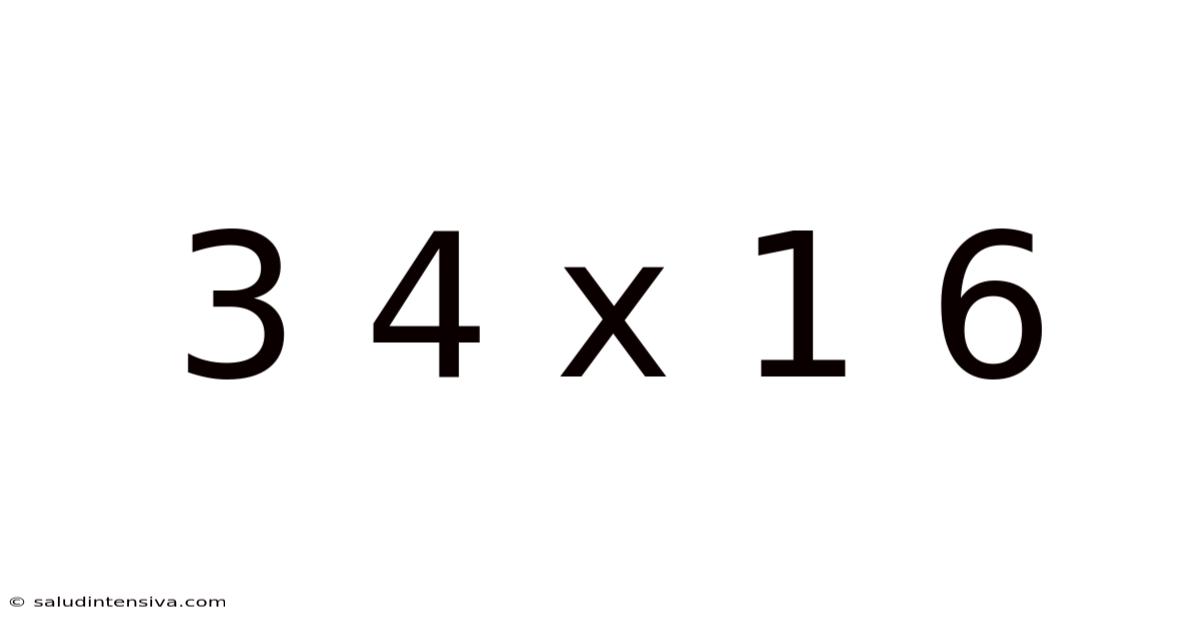
Table of Contents
Decoding 3/4 x 1/6: A Deep Dive into Fraction Multiplication
Understanding fraction multiplication can seem daunting at first, but with a systematic approach, it becomes surprisingly straightforward. This article will guide you through the process of multiplying 3/4 by 1/6, explaining not only the mechanics but also the underlying mathematical principles. We'll explore various methods, address common misconceptions, and provide ample practice opportunities to solidify your understanding. This comprehensive guide will equip you with the confidence to tackle any fraction multiplication problem.
Understanding Fractions: A Quick Refresher
Before diving into the multiplication itself, let's revisit the fundamental concept of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating the number of parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) tells us we have three parts, and the denominator (4) tells us the whole is divided into four equal parts.
Method 1: Multiplying Numerators and Denominators Directly
The simplest method for multiplying fractions involves multiplying the numerators together and the denominators together separately. Let's apply this to our problem, 3/4 x 1/6:
- Multiply the numerators: 3 x 1 = 3
- Multiply the denominators: 4 x 6 = 24
- Combine the results: The product is 3/24.
This is a correct answer, but it's not in its simplest form. We need to simplify the fraction.
Simplifying Fractions: Finding the Greatest Common Factor (GCF)
Simplifying a fraction means reducing it to its lowest terms. This is done by finding the greatest common factor (GCF) of the numerator and denominator and dividing both by it. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder.
In our example, 3/24:
- Find the factors of 3: 1 and 3
- Find the factors of 24: 1, 2, 3, 4, 6, 8, 12, and 24
- Identify the GCF: The largest number that appears in both lists is 3.
- Divide both the numerator and denominator by the GCF: 3 ÷ 3 = 1 and 24 ÷ 3 = 8
Therefore, the simplified fraction is 1/8. So, 3/4 x 1/6 = 1/8.
Method 2: Simplifying Before Multiplying (Cancellation)
A more efficient approach is to simplify the fractions before multiplying. This method, often called cancellation, involves identifying common factors between the numerators and denominators and canceling them out.
Let's revisit 3/4 x 1/6:
Notice that the numerator 3 and the denominator 6 share a common factor of 3. We can simplify this before multiplying:
- Identify common factors: 3/3 = 1 and 6/3 = 2
- Cancel the common factors: The fraction becomes (3/3) x (1/6/3) = 1/4 x 1/2
- Multiply the simplified fractions: 1 x 1 = 1 and 4 x 2 = 8
- Result: The product is 1/8.
This method yields the same result (1/8) but with fewer steps, especially when dealing with larger fractions.
Visual Representation: Understanding Fraction Multiplication Geometrically
Visualizing fraction multiplication can enhance understanding. Imagine a rectangle representing the whole. Let's illustrate 3/4 x 1/6:
- Represent 3/4: Divide the rectangle into four equal parts and shade three of them.
- Represent 1/6: Divide the shaded area (representing 3/4) into six equal parts horizontally.
- Find the overlapping area: The overlapping area represents the product. You'll find that one out of eight equal parts of the original rectangle is doubly shaded.
This visual representation confirms that 3/4 x 1/6 = 1/8.
The Commutative Property of Multiplication: Order Doesn't Matter
The commutative property states that the order of numbers in multiplication doesn't affect the result. This applies to fractions as well. Therefore, 3/4 x 1/6 is the same as 1/6 x 3/4. You can use either order when calculating the product.
Real-World Applications: Where Do We Use Fraction Multiplication?
Fraction multiplication is crucial in many real-world scenarios:
- Cooking and Baking: Adjusting recipes, scaling ingredients up or down.
- Construction and Engineering: Calculating material quantities, measuring distances.
- Finance: Calculating percentages, proportions, and interest.
- Science: Determining concentrations, ratios, and probabilities.
Understanding fraction multiplication is a fundamental skill with broad applications.
Addressing Common Misconceptions
Several common misconceptions surround fraction multiplication:
- Adding instead of multiplying: Remember, fraction multiplication involves multiplying numerators and multiplying denominators, not adding them.
- Forgetting to simplify: Always simplify the resulting fraction to its lowest terms.
- Incorrect cancellation: Ensure you are canceling common factors between the numerator of one fraction and the denominator of the other, not within the same fraction.
Practice Problems
Here are some practice problems to solidify your understanding:
- 2/5 x 1/3
- 5/8 x 2/5
- 3/7 x 4/9
- 1/2 x 1/2
- 4/5 x 5/6
Frequently Asked Questions (FAQ)
Q: Can I multiply mixed numbers directly?
A: No. First, convert mixed numbers into improper fractions (where the numerator is greater than or equal to the denominator) before multiplying. For example, 1 1/2 becomes 3/2.
Q: What if the fractions have different denominators?
A: You don't need to find a common denominator when multiplying fractions. Simply multiply the numerators and the denominators separately.
Q: What happens if I multiply a fraction by 1?
A: Multiplying a fraction by 1 doesn't change its value. The result remains the same.
Q: Why is simplification important?
A: Simplifying fractions makes the answer easier to understand and compare. It provides a clear and concise representation of the value.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a vital step in building a solid foundation in mathematics. By understanding the underlying principles, utilizing efficient methods like cancellation, and practicing regularly, you can confidently tackle any fraction multiplication problem. Remember the key steps: multiply the numerators, multiply the denominators, and always simplify your answer to its lowest terms. With practice and a clear understanding of the concepts, fraction multiplication will become second nature. Don't be afraid to revisit the visual representations and explanations whenever you encounter difficulties. The more you practice, the more confident and proficient you'll become. Remember, every mathematical concept, even seemingly complex ones like fraction multiplication, can be mastered with dedication and the right approach.
Latest Posts
Latest Posts
-
Gcf Of 9 And 14
Sep 16, 2025
-
Equivalent Fraction Of 8 12
Sep 16, 2025
-
Lcm Of 20 And 6
Sep 16, 2025
-
Square Feet To Cm Calculator
Sep 16, 2025
-
1 4 As A Mixed Number
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 4 X 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.