Equivalent Fraction Of 8 12
saludintensiva
Sep 16, 2025 · 6 min read
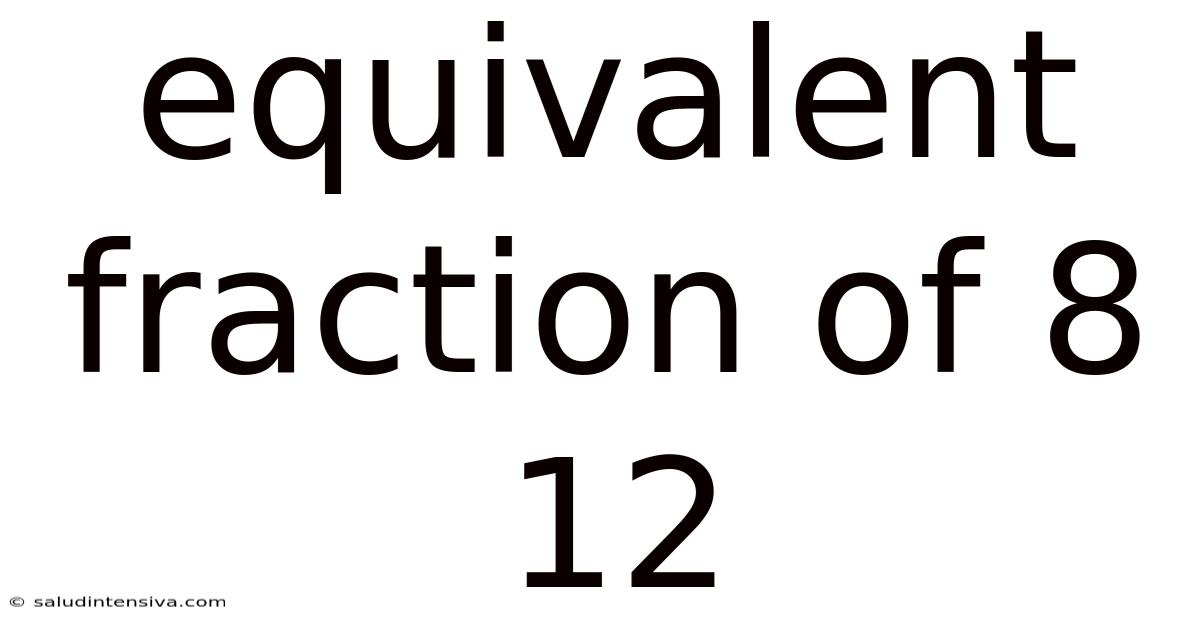
Table of Contents
Understanding Equivalent Fractions: A Deep Dive into 8/12
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding proportions, ratios, and simplifying complex expressions. This article will provide a comprehensive guide to understanding equivalent fractions, using the example of 8/12. We'll explore the concept, demonstrate various methods for finding equivalent fractions, delve into the underlying mathematical principles, and address frequently asked questions. This will equip you with the knowledge and skills to confidently tackle equivalent fraction problems of any complexity.
What are Equivalent Fractions?
Equivalent fractions represent the same portion or value, even though they appear different. They are essentially different ways of expressing the same ratio. Think of slicing a pizza: one-half (1/2) is the same as two-quarters (2/4) or four-eighths (4/8), even though the number of slices varies. These are all equivalent fractions. In our case, we'll explore equivalent fractions for 8/12. This means we're looking for fractions that represent the same part of a whole as 8/12.
Methods for Finding Equivalent Fractions of 8/12
There are several ways to find equivalent fractions, and we'll explore each with reference to 8/12:
1. Multiplying the Numerator and Denominator by the Same Number:
The most straightforward method involves multiplying both the numerator (top number) and the denominator (bottom number) of the fraction by the same non-zero number. This is based on the fundamental principle that multiplying a number by 1 doesn't change its value. Since any number divided by itself equals 1, multiplying a fraction by a cleverly disguised '1' (like 2/2 or 3/3) preserves its value.
Let's apply this to 8/12:
- Multiplying by 2/2: (8 x 2) / (12 x 2) = 16/24
- Multiplying by 3/3: (8 x 3) / (12 x 3) = 24/36
- Multiplying by 4/4: (8 x 4) / (12 x 4) = 32/48
These fractions – 16/24, 24/36, 32/48, and so on – are all equivalent to 8/12. We can generate infinitely many equivalent fractions using this method.
2. Dividing the Numerator and Denominator by the Same Number (Simplifying Fractions):
The reverse process, dividing both the numerator and denominator by the same non-zero number (their greatest common divisor), simplifies the fraction to its lowest terms. This is also known as finding the simplest form or reduced form. This process doesn't create new equivalent fractions, but it reveals the most concise representation of the existing fraction.
To simplify 8/12, we need to find the greatest common divisor (GCD) of 8 and 12. The GCD is 4.
- Dividing by 4/4: (8 ÷ 4) / (12 ÷ 4) = 2/3
Therefore, 2/3 is the simplest form of 8/12. It's still an equivalent fraction, just a more efficient representation.
3. Using Visual Representations:
Visual aids, such as diagrams or shapes, can help understand equivalent fractions intuitively. Imagine a rectangular shape divided into 12 equal parts. Shading 8 of these parts represents the fraction 8/12. You can then divide this shape into different numbers of equal parts while maintaining the shaded proportion, thus visually demonstrating equivalent fractions. For instance, dividing the shape into 6 equal parts will leave 4 parts shaded, representing the equivalent fraction 4/6. Similarly, dividing it into 3 equal parts will give you 2/3 shaded area.
The Mathematical Principle Behind Equivalent Fractions
The fundamental principle underpinning equivalent fractions is the concept of proportionality. Two fractions are equivalent if their ratios are equal. This can be expressed mathematically as:
a/b = c/d if and only if a x d = b x c
Let's test this with 8/12 and its simplified form 2/3:
- 8 x 3 = 24
- 12 x 2 = 24
Since the cross-products are equal, we confirm that 8/12 and 2/3 are equivalent fractions. This principle holds true for any pair of equivalent fractions.
Applications of Equivalent Fractions
Understanding equivalent fractions is essential in various mathematical contexts:
- Simplifying fractions: Reducing fractions to their simplest form makes calculations easier and helps in comparing fractions.
- Adding and subtracting fractions: Before adding or subtracting fractions, we often need to find a common denominator. This involves finding equivalent fractions with the same denominator.
- Solving proportions: Many real-world problems involve proportions, such as scaling recipes or calculating ratios in mixtures. Equivalent fractions are crucial in solving these problems.
- Understanding ratios and percentages: Fractions, ratios, and percentages are closely related, and equivalent fractions are instrumental in converting between these forms.
- Geometry and measurement: Equivalent fractions are used in various geometrical calculations, such as finding areas and volumes.
Frequently Asked Questions (FAQ)
Q1: How do I know if two fractions are equivalent?
A1: You can check if two fractions, a/b and c/d, are equivalent by cross-multiplying: if a x d = b x c, then the fractions are equivalent. Alternatively, you can simplify both fractions to their lowest terms. If they simplify to the same fraction, they are equivalent.
Q2: Can a fraction have multiple equivalent fractions?
A2: Yes, a fraction can have infinitely many equivalent fractions. You can generate them by multiplying the numerator and denominator by any non-zero number.
Q3: What is the simplest form of a fraction?
A3: The simplest form of a fraction is when the numerator and denominator have no common factors other than 1. It's obtained by dividing both the numerator and denominator by their greatest common divisor (GCD).
Q4: Why is simplifying fractions important?
A4: Simplifying fractions makes them easier to work with in calculations, comparisons, and understanding their value. It presents the fraction in its most concise and efficient representation.
Q5: How can I find the greatest common divisor (GCD)?
A5: There are several methods to find the GCD, including: * Listing factors: List all factors of both numbers and identify the largest common factor. * Prime factorization: Express both numbers as a product of their prime factors. The GCD is the product of the common prime factors raised to the lowest power. * Euclidean algorithm: A more efficient method for larger numbers, involving repeated division with remainder.
Conclusion
Understanding equivalent fractions is a cornerstone of mathematical literacy. By mastering the different methods for finding and simplifying equivalent fractions, you build a strong foundation for more advanced mathematical concepts. The example of 8/12 has served as a practical illustration of these principles, highlighting the importance of simplifying fractions and the underlying mathematical relationships. Remember that the ability to confidently work with equivalent fractions is crucial for success in various mathematical and real-world applications. Practice consistently, and you'll soon find yourself effortlessly navigating the world of fractions.
Latest Posts
Latest Posts
-
What Are Multiples Of Seven
Sep 16, 2025
-
Whats 4 3 As A Decimal
Sep 16, 2025
-
Lcm Of 6 And 27
Sep 16, 2025
-
Gcf Of 4 And 20
Sep 16, 2025
-
10 12 In Simplest Form
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Equivalent Fraction Of 8 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.