Lcm Of 20 And 6
saludintensiva
Sep 16, 2025 · 5 min read
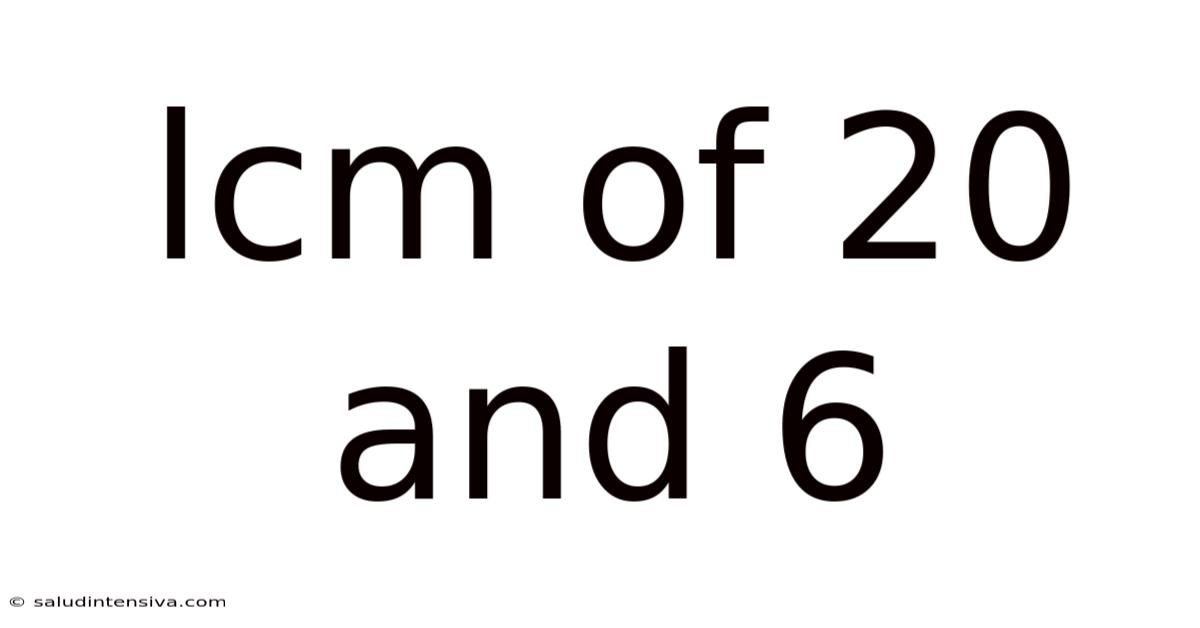
Table of Contents
Finding the Least Common Multiple (LCM) of 20 and 6: A Comprehensive Guide
Understanding the Least Common Multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This article will delve deep into finding the LCM of 20 and 6, exploring multiple methods and providing a thorough understanding of the underlying principles. We'll move beyond a simple answer and explore the "why" behind the calculations, ensuring you grasp the concept completely.
Introduction: What is LCM?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. Think of it as the smallest number that contains all the factors of the numbers you're working with. For example, if you're considering the LCM of 2 and 3, the answer is 6 because 6 is the smallest number that is divisible by both 2 and 3. This concept is vital in various mathematical operations, including fraction simplification, finding common denominators, and solving problems related to cyclical events.
Method 1: Prime Factorization
This method is considered the most robust and conceptually clear way to find the LCM. It involves breaking down each number into its prime factors – the fundamental building blocks of numbers that are only divisible by 1 and themselves. Let's apply this to find the LCM of 20 and 6:
-
Find the prime factorization of each number:
- 20 = 2 x 2 x 5 = 2² x 5
- 6 = 2 x 3
-
Identify common and uncommon prime factors: We see that both 20 and 6 share a common prime factor of 2. However, 20 also has a factor of 5, and 6 has a factor of 3.
-
Construct the LCM: To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
- The highest power of 2 is 2² (from the factorization of 20).
- The highest power of 3 is 3¹ (from the factorization of 6).
- The highest power of 5 is 5¹ (from the factorization of 20).
Therefore, LCM(20, 6) = 2² x 3 x 5 = 4 x 3 x 5 = 60
Method 2: Listing Multiples
This is a more intuitive but less efficient method, especially when dealing with larger numbers. It involves listing the multiples of each number until you find the smallest multiple common to both.
-
List the multiples of 20: 20, 40, 60, 80, 100, 120...
-
List the multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 72...
-
Identify the smallest common multiple: Notice that 60 is the smallest number that appears in both lists. Therefore, LCM(20, 6) = 60.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a handy formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
Let's apply this to find the LCM of 20 and 6:
-
Find the GCD of 20 and 6: We can use the Euclidean algorithm or prime factorization to find the GCD. Let's use prime factorization:
- 20 = 2² x 5
- 6 = 2 x 3
The only common prime factor is 2¹, so GCD(20, 6) = 2.
-
Apply the formula:
LCM(20, 6) = (|20 x 6|) / GCD(20, 6) = 120 / 2 = 60
Explanation of the Methods and Their Applicability
Each method offers a unique approach to finding the LCM. The prime factorization method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers or multiple numbers. It provides a strong conceptual understanding of the LCM by breaking down the numbers into their fundamental building blocks. The listing multiples method is more intuitive but becomes cumbersome with larger numbers. The GCD method is efficient if you already know the GCD, leveraging the strong mathematical relationship between LCM and GCD. Choosing the best method depends on the context and the complexity of the problem.
Real-World Applications of LCM
The concept of LCM isn't confined to theoretical mathematics. It finds practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses depart from the same station, one every 20 minutes and the other every 6 minutes. The LCM (60 minutes) tells you when both buses will depart simultaneously again. This principle extends to scheduling meetings, shifts, or any cyclical events.
-
Fraction Operations: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators. This ensures you can perform the arithmetic correctly.
-
Gear Ratios: In mechanical engineering, gear ratios are often expressed using LCM to determine the optimal gear combinations for specific applications.
-
Music Theory: LCM plays a role in music theory, specifically in determining the least common multiple of note durations to find rhythmic patterns.
Frequently Asked Questions (FAQ)
-
What if one of the numbers is 0? The LCM of any number and 0 is undefined because 0 has infinitely many multiples.
-
What if the numbers are negative? We usually consider only positive integers when finding the LCM. If you encounter negative numbers, take their absolute values before calculating the LCM.
-
Can I use a calculator to find the LCM? Many scientific calculators and online calculators have built-in functions to calculate the LCM of two or more numbers.
-
How do I find the LCM of more than two numbers? The prime factorization method extends easily to multiple numbers. Find the prime factorization of each number, take the highest power of each prime factor present, and multiply them together.
Conclusion: Mastering the LCM
Understanding and calculating the LCM is a valuable skill in mathematics. This comprehensive guide has explored three different methods, highlighting their strengths and weaknesses. Whether you prefer the visual appeal of listing multiples, the methodical approach of prime factorization, or the elegant efficiency of the GCD method, mastering the LCM opens doors to a deeper understanding of number theory and its real-world applications. Remember that the core concept remains consistent across all methods: finding the smallest positive integer divisible by all the given numbers. By understanding the underlying principles and practicing the different methods, you will confidently tackle LCM problems of any complexity.
Latest Posts
Latest Posts
-
7 40 As A Decimal
Sep 16, 2025
-
What Are Multiples Of Seven
Sep 16, 2025
-
Whats 4 3 As A Decimal
Sep 16, 2025
-
Lcm Of 6 And 27
Sep 16, 2025
-
Gcf Of 4 And 20
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 20 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.