What Is 2/5 + 2/3
saludintensiva
Sep 16, 2025 · 5 min read
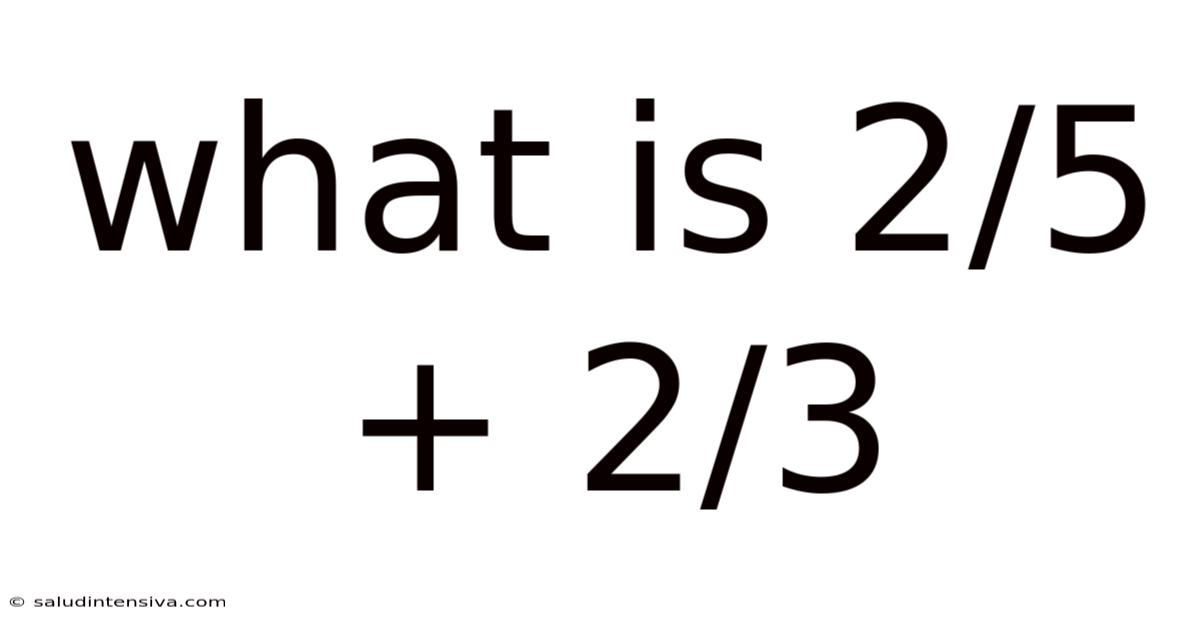
Table of Contents
Decoding Fractions: A Deep Dive into 2/5 + 2/3
Adding fractions might seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will guide you through the step-by-step solution of 2/5 + 2/3, explaining not only the mechanics but also the underlying mathematical concepts. By the end, you'll not only know the answer but also possess a solid foundation for tackling more complex fraction addition problems. This comprehensive guide is perfect for students, teachers, or anyone looking to refresh their understanding of basic arithmetic.
Understanding Fractions: A Quick Refresher
Before we dive into the addition problem, let's briefly review the components of a fraction. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number, representing the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 2/5, the numerator is 2 and the denominator is 5. This means we have 2 out of 5 equal parts.
Why Can't We Simply Add Numerators and Denominators?
A common mistake when adding fractions is to simply add the numerators and the denominators. This is incorrect. Imagine you have 2/5 of a pizza and 2/3 of another pizza. You can't simply say you have 4/8 of a pizza. The sizes of the slices are different – fifths and thirds are not the same size. To add them correctly, we need a common denominator.
Finding the Least Common Denominator (LCD)
The key to adding fractions with different denominators is finding the least common denominator (LCD). The LCD is the smallest number that is a multiple of both denominators. There are several ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find the smallest number that appears in both lists. For 5 and 3:
- Multiples of 5: 5, 10, 15, 20, 25...
- Multiples of 3: 3, 6, 9, 12, 15, 18... The smallest common multiple is 15.
-
Prime Factorization: This method is particularly useful for larger numbers. Break down each denominator into its prime factors:
- 5 = 5 (5 is a prime number)
- 3 = 3 (3 is a prime number) Then, multiply the unique prime factors together: 5 x 3 = 15. This gives us the LCD.
Converting Fractions to Equivalent Fractions
Once we have the LCD (which is 15 in this case), we need to convert both fractions so they have this common denominator. We do this by multiplying both the numerator and the denominator of each fraction by the same number. This doesn't change the value of the fraction, only its representation.
-
Converting 2/5: To get a denominator of 15, we need to multiply 5 by 3. Therefore, we must also multiply the numerator by 3: (2 x 3) / (5 x 3) = 6/15
-
Converting 2/3: To get a denominator of 15, we need to multiply 3 by 5. Therefore, we must also multiply the numerator by 5: (2 x 5) / (3 x 5) = 10/15
Adding the Fractions
Now that both fractions have the same denominator, we can simply add the numerators:
6/15 + 10/15 = (6 + 10) / 15 = 16/15
Simplifying the Result (Improper Fractions and Mixed Numbers)
The result, 16/15, is an improper fraction because the numerator (16) is larger than the denominator (15). We can convert this to a mixed number, which combines a whole number and a fraction.
To do this, we divide the numerator by the denominator:
16 ÷ 15 = 1 with a remainder of 1
This means that 16/15 is equal to 1 and 1/15.
Therefore, the final answer to 2/5 + 2/3 is 1 and 1/15 or 1 1/15.
Step-by-Step Summary: 2/5 + 2/3
- Find the LCD: The least common denominator of 5 and 3 is 15.
- Convert to Equivalent Fractions:
- 2/5 becomes 6/15 (multiply numerator and denominator by 3)
- 2/3 becomes 10/15 (multiply numerator and denominator by 5)
- Add the Fractions: 6/15 + 10/15 = 16/15
- Simplify (if necessary): 16/15 is an improper fraction, which simplifies to the mixed number 1 1/15.
Visual Representation
Imagine two separate pizzas. One is cut into 5 equal slices, and you have 2 of them (2/5). The other is cut into 3 equal slices, and you have 2 of those (2/3). To compare them easily, imagine cutting both pizzas into 15 equal slices (LCD=15). The first pizza would now have 6 slices (6/15), and the second would have 10 slices (10/15). Together, you'd have 16 slices out of 15, or 1 whole pizza and 1/15 of a pizza.
Frequently Asked Questions (FAQ)
-
Q: What if the denominators have a common factor other than 1? A: You still need to find the LCD, but you can simplify the process using prime factorization. This helps avoid unnecessary calculations.
-
Q: Can I add fractions with different denominators without finding the LCD? A: No, you cannot directly add fractions with unlike denominators. The denominators represent the size of the parts, and they must be the same for meaningful addition.
-
Q: What if I get a different LCD? A: As long as the number you find is a common multiple of both denominators, your answer will still be correct, although it may require further simplification. The LCD ensures the simplest representation.
-
Q: Why is it important to simplify improper fractions? A: Simplifying improper fractions to mixed numbers provides a clearer and more understandable representation of the result. It allows us to grasp the magnitude of the answer more easily.
Conclusion
Adding fractions might initially seem complex, but by following the steps outlined above – finding the LCD, converting fractions to equivalent fractions with the same denominator, adding the numerators, and simplifying the result – you can confidently tackle any fraction addition problem. Remember the core concept: we're combining parts of wholes, and those parts must be the same size (same denominator) before we can accurately add them. Mastering this fundamental skill is crucial for further progress in mathematics, laying the groundwork for more advanced concepts. With practice, this process will become second nature, allowing you to solve such problems quickly and accurately.
Latest Posts
Latest Posts
-
Gcf Of 9 And 14
Sep 16, 2025
-
Equivalent Fraction Of 8 12
Sep 16, 2025
-
Lcm Of 20 And 6
Sep 16, 2025
-
Square Feet To Cm Calculator
Sep 16, 2025
-
1 4 As A Mixed Number
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 + 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.