Simplest Form Of 12 15
saludintensiva
Sep 16, 2025 · 5 min read
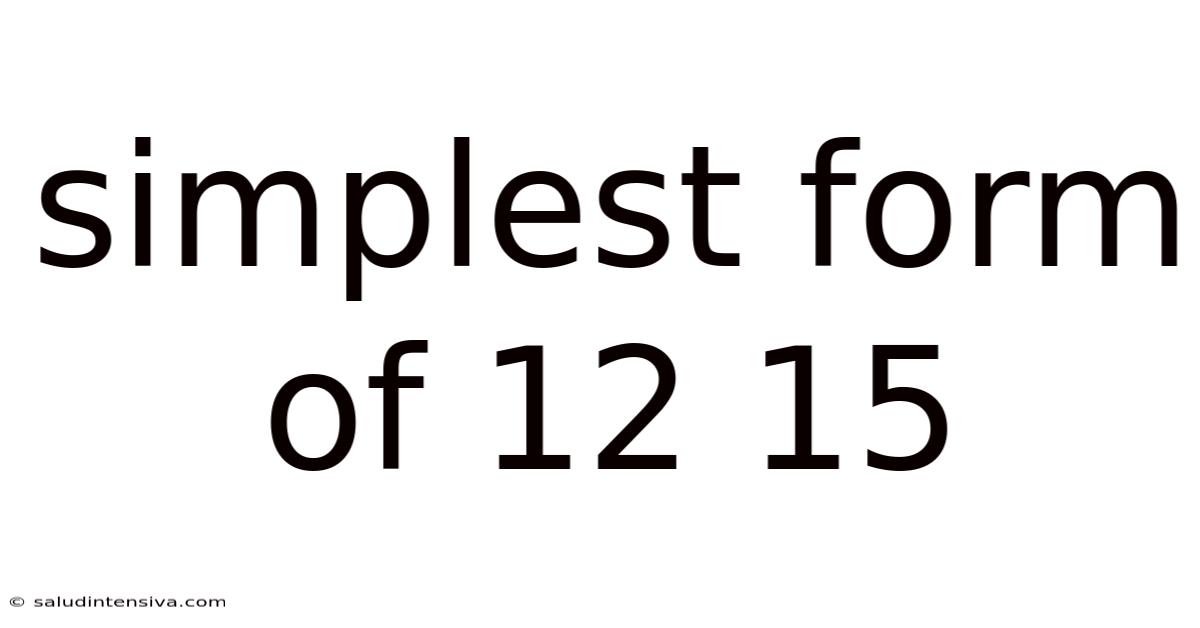
Table of Contents
Finding the Simplest Form of 12/15: A Comprehensive Guide
Finding the simplest form of a fraction, also known as reducing or simplifying a fraction, is a fundamental concept in mathematics. This guide will walk you through the process of simplifying the fraction 12/15, explaining the underlying principles and providing a deeper understanding of fraction simplification. We'll cover the core concept, various methods, and even delve into the mathematical reasoning behind it. By the end, you'll not only know the simplest form of 12/15 but also be equipped to simplify any fraction with confidence.
Understanding Fractions and Simplification
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The fraction 12/15 means 12 parts out of a total of 15 parts. Simplifying a fraction means expressing it in its lowest terms, where the numerator and denominator have no common factors other than 1. This doesn't change the value of the fraction; it just represents it in a more concise and manageable way. Think of it like reducing a recipe – you can halve or quarter the ingredients, but the final dish will taste the same.
Method 1: Finding the Greatest Common Divisor (GCD)
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. Once you find the GCD, you divide both the numerator and the denominator by it.
Let's apply this to 12/15:
- Find the factors of 12: 1, 2, 3, 4, 6, 12
- Find the factors of 15: 1, 3, 5, 15
- Identify the common factors: 1 and 3
- The greatest common factor (GCF) is 3.
Now, divide both the numerator and the denominator by the GCD:
12 ÷ 3 = 4 15 ÷ 3 = 5
Therefore, the simplest form of 12/15 is 4/5.
Method 2: Step-by-Step Division by Common Factors
If you don't immediately see the GCD, you can simplify the fraction step-by-step by dividing both the numerator and denominator by any common factor you find. You repeat this process until no common factors remain.
Let's simplify 12/15 using this method:
- Notice that both 12 and 15 are divisible by 3.
- Divide both by 3: 12 ÷ 3 = 4 and 15 ÷ 3 = 5. This gives us 4/5.
- Since 4 and 5 have no common factors other than 1, we have reached the simplest form.
Again, the simplest form of 12/15 is 4/5.
Method 3: Prime Factorization
Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). This method is particularly useful for larger numbers where finding the GCD directly might be challenging.
-
Find the prime factorization of 12: 2 x 2 x 3 (or 2² x 3)
-
Find the prime factorization of 15: 3 x 5
-
Identify the common prime factors: 3 is the only common prime factor.
-
Cancel out the common prime factors: (2 x 2 x 3) / (3 x 5) The 3 cancels out from both the numerator and the denominator.
-
The simplified fraction is: (2 x 2) / 5 = 4/5
This confirms once more that the simplest form of 12/15 is 4/5.
Why Simplification Matters
Simplifying fractions is crucial for several reasons:
- Clarity: Simpler fractions are easier to understand and interpret. 4/5 is much clearer than 12/15.
- Calculations: Simplifying fractions before performing operations (like addition, subtraction, multiplication, or division) makes calculations significantly easier and less prone to errors.
- Comparisons: Comparing simplified fractions is much simpler than comparing unsimplified ones. It's easy to see that 4/5 is greater than 1/2, but comparing 12/15 to 1/2 requires more effort.
- Real-world applications: Fractions are used extensively in various fields, from cooking and construction to finance and engineering. Simplified fractions ensure accuracy and efficiency in these applications.
Further Exploration: Equivalent Fractions
It's important to understand that a simplified fraction is equivalent to the original fraction. This means they represent the same value. Many fractions can be equivalent to 4/5. For example:
- 8/10 (multiply both numerator and denominator by 2)
- 12/15 (multiply both numerator and denominator by 3)
- 16/20 (multiply both numerator and denominator by 4)
- and so on...
All these fractions, when simplified, will result in 4/5.
Frequently Asked Questions (FAQs)
Q1: What if the numerator and denominator have no common factors other than 1?
A1: If the numerator and denominator share no common factors besides 1, the fraction is already in its simplest form. For instance, 7/11 is already in its simplest form.
Q2: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
A2: No. You must divide both the numerator and denominator by the same number to maintain the value of the fraction. Dividing by different numbers will change the value.
Q3: Is there a shortcut for finding the GCD?
A3: While prime factorization is a robust method, for smaller numbers, you can often identify the GCD by inspection. Look for common factors between the numerator and denominator. If you struggle to find the GCD quickly, using the Euclidean algorithm is a reliable alternative method.
Q4: Why is simplifying important in real-world problems?
A4: In practical applications, simplified fractions lead to more efficient calculations and easier interpretation of results. Imagine working with a recipe that uses fractions like 12/15 cups of flour – simplifying to 4/5 makes the measurement clearer and easier to handle. Similarly, in construction or engineering, simplified fractions can lead to more precise measurements and calculations.
Conclusion
Simplifying fractions, while a seemingly basic mathematical concept, is fundamental to a solid understanding of fractions and their applications. Mastering the various methods – using the GCD, step-by-step division, or prime factorization – empowers you to work efficiently with fractions, improving accuracy and clarity in both mathematical problems and real-world applications. The simplest form of 12/15, as we've demonstrated through multiple methods, is definitively 4/5. Remember the key is finding the greatest common divisor and dividing both the numerator and the denominator by it. This simple process opens the door to a more profound understanding of fractions and their importance in various fields.
Latest Posts
Latest Posts
-
Gcf Of 9 And 14
Sep 16, 2025
-
Equivalent Fraction Of 8 12
Sep 16, 2025
-
Lcm Of 20 And 6
Sep 16, 2025
-
Square Feet To Cm Calculator
Sep 16, 2025
-
1 4 As A Mixed Number
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Simplest Form Of 12 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.