2 5/8 Divided By 1/2
saludintensiva
Sep 19, 2025 · 6 min read
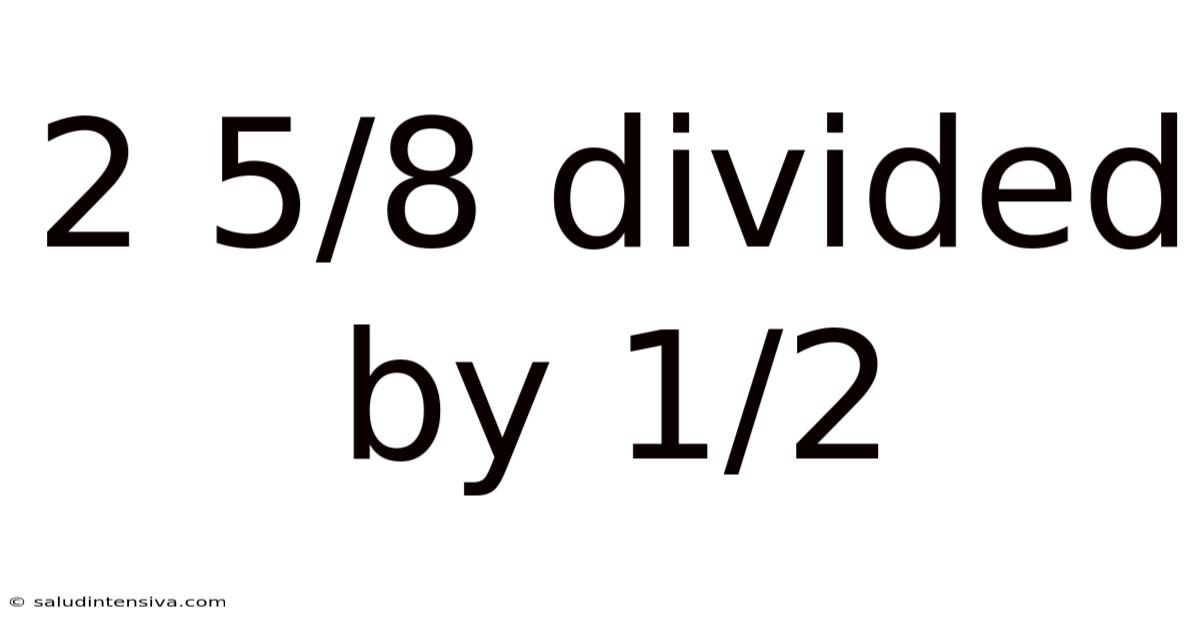
Table of Contents
Diving Deep into Division: Solving 2 5/8 Divided by 1/2
Dividing fractions and mixed numbers can seem daunting, but with a clear understanding of the process, it becomes surprisingly straightforward. This article will guide you through solving the problem "2 5/8 divided by 1/2," not just providing the answer, but also explaining the underlying mathematical principles and offering various approaches to tackle similar problems. This comprehensive guide aims to build your confidence in tackling fraction division, equipping you with the skills to solve even more complex problems.
Understanding the Fundamentals: Fractions and Division
Before diving into the specific problem, let's refresh our understanding of fractions and division. A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator shows how many of those parts are being considered.
Division, in its simplest form, is about finding out how many times one number (the divisor) goes into another number (the dividend). When dealing with fractions, this concept remains the same, but the process requires a slightly different approach.
Converting Mixed Numbers to Improper Fractions
Our problem involves a mixed number, 2 5/8. A mixed number combines a whole number and a fraction. To make division easier, we need to convert this mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
To convert 2 5/8 to an improper fraction:
- Multiply the whole number by the denominator: 2 * 8 = 16
- Add the numerator to the result: 16 + 5 = 21
- Keep the same denominator: The denominator remains 8.
Therefore, 2 5/8 is equivalent to the improper fraction 21/8.
The Reciprocal: The Key to Fraction Division
The core principle of dividing fractions involves using the reciprocal of the divisor. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/2 is 2/1 (or simply 2).
Solving 2 5/8 Divided by 1/2: Step-by-Step
Now, we can rewrite our problem using the improper fraction: 21/8 ÷ 1/2. Here's the step-by-step solution:
-
Convert the mixed number to an improper fraction: As shown above, 2 5/8 becomes 21/8.
-
Replace division with multiplication and use the reciprocal: Instead of dividing by 1/2, we multiply by its reciprocal, 2/1 (or 2). So, the problem becomes: 21/8 * 2/1.
-
Multiply the numerators and the denominators: Multiply the numerators together (21 * 2 = 42) and the denominators together (8 * 1 = 8). This gives us the fraction 42/8.
-
Simplify the fraction (if possible): The fraction 42/8 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 42 and 8 is 2. Divide both the numerator and the denominator by 2: 42 ÷ 2 = 21 and 8 ÷ 2 = 4.
This gives us the simplified improper fraction 21/4.
-
Convert the improper fraction back to a mixed number (optional): While 21/4 is a perfectly acceptable answer, we can convert it back to a mixed number for easier understanding. To do this, divide the numerator (21) by the denominator (4):
- 21 ÷ 4 = 5 with a remainder of 1.
This means that 21/4 is equal to 5 1/4.
Therefore, 2 5/8 divided by 1/2 equals 5 1/4.
Alternative Approaches and Visualizations
While the method above is the standard approach, let's explore some alternative methods to solidify your understanding.
1. Visual Representation:
Imagine you have 2 pizzas and 5/8 of another pizza. You want to divide this total amount among half a person (1/2). Visualizing this will help you understand that you will end up with more than 2 full servings. This helps connect the abstract concept of fraction division to a tangible scenario.
2. Using Decimal Conversion:
Another approach involves converting the fractions to decimals.
- 2 5/8 = 2.625
- 1/2 = 0.5
Then perform the division: 2.625 ÷ 0.5 = 5.25. Converting 5.25 back to a fraction gives us 5 1/4. This method is useful for those more comfortable with decimal calculations. However, it's crucial to remember that rounding errors can occur with decimal conversions, especially with more complex fractions.
Why This Method Works: A Deeper Dive into Mathematical Principles
The method we used relies on the fundamental properties of fractions and division. When dividing by a fraction, we essentially multiply by its reciprocal. This works because division is the inverse operation of multiplication. Dividing by 1/2 is the same as multiplying by 2 because two halves make a whole. This principle applies to all fraction divisions.
Frequently Asked Questions (FAQ)
Q1: Why do we use the reciprocal when dividing fractions?
A1: We use the reciprocal because division is the inverse of multiplication. Multiplying by the reciprocal "undoes" the division, giving us the correct result.
Q2: Can I solve this problem using a calculator?
A2: Yes, most calculators can handle fraction division. However, understanding the underlying mathematical principles is crucial for solving more complex problems and for developing strong mathematical reasoning skills.
Q3: What if I have more than two fractions in the problem?
A3: If you have multiple fractions, convert all mixed numbers to improper fractions, then proceed with the same steps. Always work from left to right, dealing with one division operation at a time. For example, (a/b) ÷ (c/d) ÷ (e/f) would be solved as ((a/b) * (d/c)) ÷ (e/f) and then as (((a/b) * (d/c)) * (f/e)).
Q4: What if the divisor is a whole number?
A4: Treat the whole number as a fraction with a denominator of 1. For example, dividing by 3 is the same as dividing by 3/1. You would then use the reciprocal (1/3) and multiply.
Conclusion: Mastering Fraction Division
Mastering fraction division empowers you to tackle a wide range of mathematical problems. This article has provided a thorough walkthrough of solving "2 5/8 divided by 1/2," but more importantly, it has equipped you with the fundamental knowledge and strategies to confidently approach any fraction division problem. Remember the key steps: convert mixed numbers to improper fractions, use the reciprocal of the divisor, multiply, simplify, and convert back to a mixed number if necessary. Practice is key—the more you work with fractions, the more intuitive this process will become. Don't be afraid to explore different approaches and visualize the problems to deepen your understanding. With consistent effort and a focused approach, conquering fraction division will become a breeze.
Latest Posts
Latest Posts
-
120 Days Back From Today
Sep 19, 2025
-
Half Of 9 1 4
Sep 19, 2025
-
Convert 175 Lbs To Kg
Sep 19, 2025
-
180 Days Back From Today
Sep 19, 2025
-
4 15 As A Percent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2 5/8 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.