4 15 As A Percent
saludintensiva
Sep 19, 2025 · 5 min read
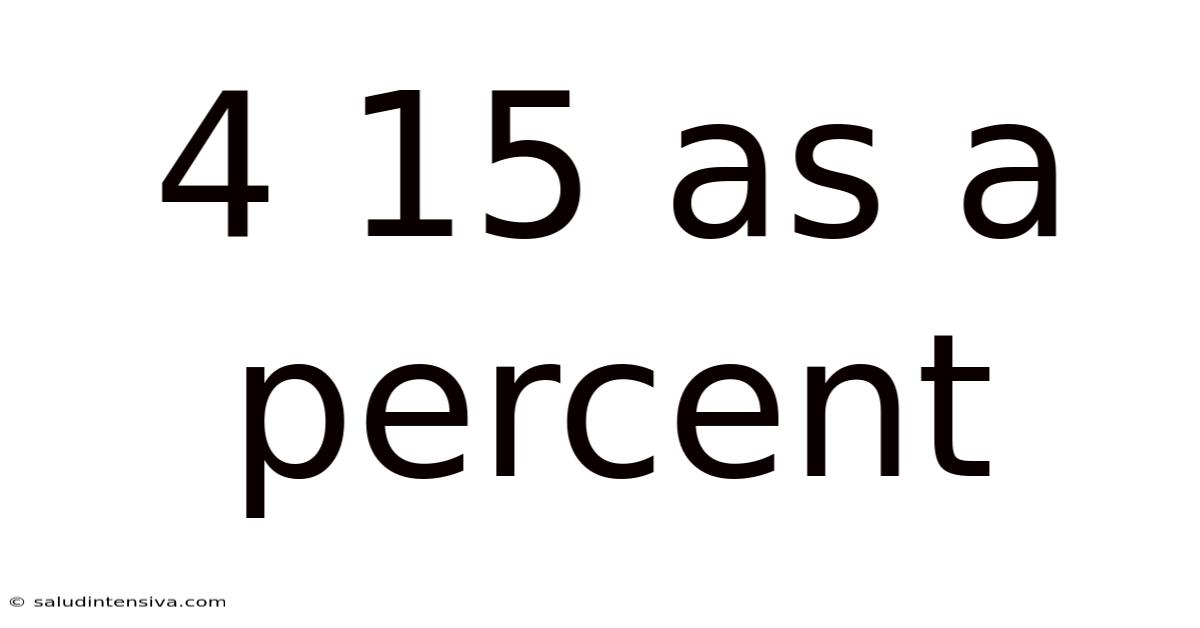
Table of Contents
Understanding 4/15 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This article provides a comprehensive guide on how to convert the fraction 4/15 into a percentage, explaining the process step-by-step and exploring the underlying mathematical concepts. We'll also delve into practical applications and answer frequently asked questions to solidify your understanding. By the end, you'll not only know the percentage equivalent of 4/15 but also possess a strong grasp of fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 4/15, 4 is the numerator and 15 is the denominator. This means we are considering 4 parts out of a total of 15 equal parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates how many parts per hundred. For instance, 25% means 25 out of 100, which is equivalent to the fraction 25/100, or simplified, 1/4.
Converting 4/15 to a Percentage: Step-by-Step Guide
There are two primary methods for converting a fraction to a percentage:
Method 1: Converting the fraction to a decimal and then to a percentage
This method involves two steps:
-
Convert the fraction to a decimal: To do this, we divide the numerator (4) by the denominator (15):
4 ÷ 15 ≈ 0.266666...
The result is a repeating decimal. We can round this to a certain number of decimal places for practical purposes. For this example, we'll use four decimal places: 0.2667.
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.2667 × 100 = 26.67%
Therefore, 4/15 is approximately equal to 26.67%.
Method 2: Finding an equivalent fraction with a denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. While sometimes more challenging than Method 1, it offers a deeper understanding of the relationship between fractions and percentages.
To find an equivalent fraction with a denominator of 100, we need to find a number that, when multiplied by 15, results in 100. Unfortunately, 100 is not evenly divisible by 15. Therefore, this method will involve working with decimals.
We can set up a proportion:
4/15 = x/100
To solve for x, we cross-multiply:
15x = 400
x = 400/15 ≈ 26.67
Therefore, 4/15 is approximately equal to 26.67%.
Understanding the Approximation
It's important to note that in both methods, we obtained an approximate value (26.67%). This is because the decimal representation of 4/15 is a repeating decimal (0.26666...). The precision of the percentage depends on how many decimal places we round to. If we needed greater accuracy, we could use more decimal places. However, for most practical purposes, 26.67% is sufficiently accurate.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in various real-life scenarios:
-
Discounts and Sales: If a store offers a 20% discount on an item, you need to understand this fraction (20/100 or 1/5) to calculate the final price.
-
Financial Calculations: Interest rates, tax calculations, and investment returns are often expressed as percentages.
-
Data Analysis: Representing data in percentages makes it easier to compare and interpret different proportions. For example, understanding the percentage of students who passed an exam is easier than interpreting it as a fraction.
-
Surveys and Polls: Results from surveys and polls are often presented as percentages to summarize the responses.
-
Everyday Life: Calculating tips, understanding ingredient proportions in recipes, and even dividing tasks fairly all involve understanding percentages.
Further Exploration: Working with Percentages
Converting percentages back to fractions or decimals is equally important. To convert a percentage to a decimal, divide by 100. To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100, and then simplify the fraction if possible. For example:
- 75% = 75/100 = 3/4
- 20% = 20/100 = 1/5
Mastering these conversions allows for seamless movement between fractions, decimals, and percentages, providing a flexible approach to problem-solving in various mathematical contexts.
Frequently Asked Questions (FAQ)
Q1: Is there a way to calculate 4/15 as a percentage without using a calculator?
A1: While a calculator simplifies the process, you can perform the division using long division. This method, although more time-consuming, helps to reinforce the fundamental principles of decimal conversion.
Q2: What if I need a more precise percentage than 26.67%?
A2: You can use more decimal places in your calculations. For example, using five decimal places would give you 26.66667%. The level of precision needed depends on the specific application.
Q3: Can I express 4/15 as a percentage with a recurring decimal?
A3: Yes, you can represent it as 26.666...% where the 6 repeats infinitely. However, for practical applications, rounding is generally preferred.
Q4: Are there other fractions that are difficult to convert to percentages?
A4: Fractions with denominators that are not factors of 100 (10, 100, 1000, etc.) will usually result in repeating or long decimal numbers when converted to percentages. The complexity arises from the difficulty in finding an equivalent fraction with a denominator of 100.
Conclusion
Converting 4/15 to a percentage, approximately 26.67%, involves a straightforward process using either decimal conversion or finding an equivalent fraction with a denominator of 100. Understanding this conversion is crucial for various applications, from everyday calculations to complex financial analysis. Mastering this skill empowers you to confidently tackle problems involving fractions and percentages, improving your mathematical fluency and problem-solving abilities. Remember, practice is key to building proficiency. Try converting other fractions to percentages to solidify your understanding and build confidence in your abilities.
Latest Posts
Latest Posts
-
Write P In Factored Form
Sep 19, 2025
-
How Big 5000 Square Feet
Sep 19, 2025
-
12 45 As A Percentage
Sep 19, 2025
-
Simplify 1 I I 1
Sep 19, 2025
-
10 X 7 X 3
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 4 15 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.