2 5 Divided By 2
saludintensiva
Sep 18, 2025 · 5 min read
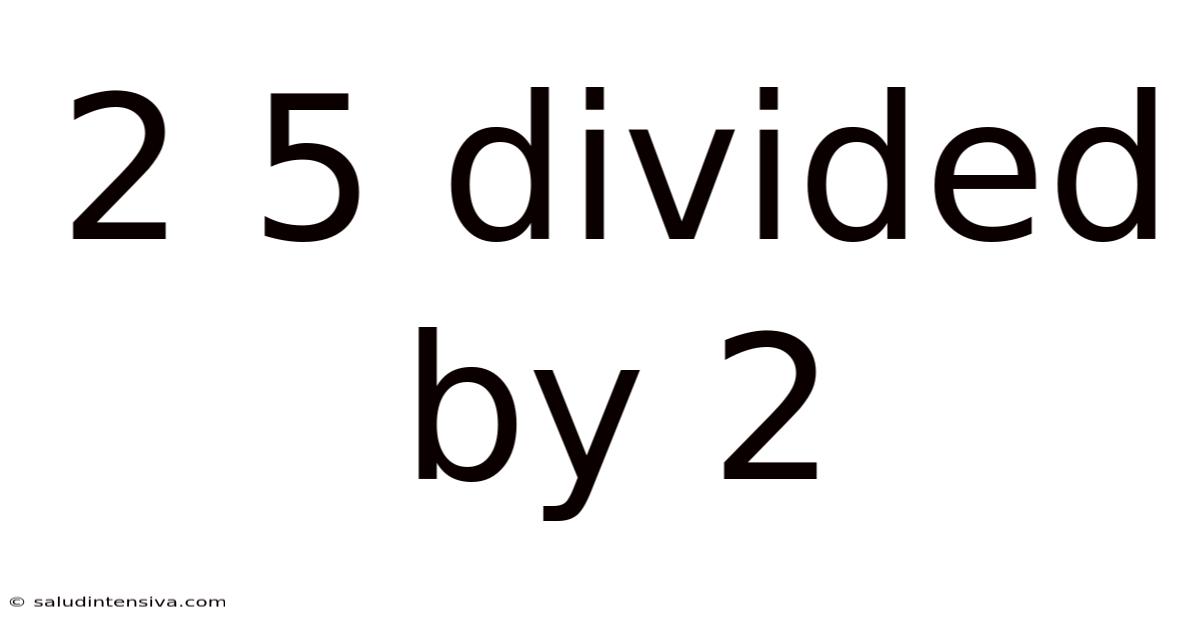
Table of Contents
Decoding 25 Divided by 2: A Deep Dive into Division and Fractions
This article explores the seemingly simple calculation of 25 divided by 2, delving far beyond the basic answer. We'll unpack the process, explore different methods for solving it, and uncover the underlying mathematical concepts, making this seemingly straightforward problem a gateway to a richer understanding of division and fractions. Understanding this calculation is crucial for mastering fundamental arithmetic, and this comprehensive guide will benefit students, educators, and anyone seeking to solidify their mathematical foundation.
Understanding Division: The Core Concept
Before diving into 25 divided by 2, let's establish a firm grasp of division itself. Division is essentially the inverse operation of multiplication. When we say "25 divided by 2," we're asking: "How many times does 2 fit into 25?" This question can be framed in several ways, highlighting the versatility of division:
- Partitioning: Dividing 25 into two equal parts.
- Repeated Subtraction: How many times can you subtract 2 from 25 before reaching zero?
- Finding the Quotient: Determining the result of sharing 25 items equally among 2 people.
Each perspective illuminates a different facet of division, emphasizing its practical application in various real-world scenarios.
Calculating 25 Divided by 2: Methods and Approaches
There are several ways to calculate 25 divided by 2, each offering unique insights into the problem:
1. Long Division: This classic method provides a step-by-step approach, suitable for understanding the process thoroughly.
12
2 | 25
2
--
05
04
--
1
This demonstrates that 2 goes into 25 twelve times with a remainder of 1. This remainder signifies that there's one unit left over after dividing 25 equally among two groups.
2. Using Fractions: Representing the division as a fraction offers an elegant solution. 25 divided by 2 can be written as 25/2. This fraction represents 25 parts out of a possible 2, which simplifies to a mixed number:
25/2 = 12 1/2 or 12.5
This clearly shows that the result is 12 and a half. This fractional representation is often preferred for its clarity and its ability to handle remainders smoothly.
3. Decimal Representation: Converting the fraction to a decimal is another common approach. Dividing 25 by 2 using a calculator or long division with decimal points gives us 12.5. This decimal form is particularly useful in scenarios requiring numerical precision, such as in measurements or calculations involving decimals.
Interpreting the Results: Remainders and Decimals
The outcome of 25 divided by 2—whether expressed as 12 with a remainder of 1, 12 1/2, or 12.5—highlights the importance of interpreting results within the context of the problem.
- Remainders: The remainder of 1 in the long division method signifies that there's an incomplete group. In a real-world scenario, this might mean one item is left over after dividing 25 items equally among 2 people.
- Fractions: The fractional representation (12 1/2) precisely shows the incomplete division. It signifies that there's an extra half of a unit.
- Decimals: The decimal representation (12.5) provides a concise, numerical way to represent the result, avoiding the ambiguity of a remainder. It's often used when dealing with continuous quantities, such as measurements.
Choosing the appropriate representation (remainder, fraction, or decimal) depends on the specific context of the problem and the level of precision required.
Expanding the Understanding: Real-World Applications
The seemingly simple calculation of 25 divided by 2 has broad applications across various fields:
- Everyday Life: Sharing items equally, dividing resources, splitting bills, calculating portions of recipes, and determining average values all involve division.
- Geometry and Measurement: Calculating areas, volumes, and lengths often necessitates dividing quantities.
- Engineering and Physics: Division plays a critical role in numerous calculations related to ratios, proportions, and rates.
- Finance and Accounting: Calculating averages, percentages, and proportions in financial data heavily utilizes division.
- Computer Science: Division forms the basis of numerous algorithms and computations in programming.
Beyond the Basics: Exploring Advanced Concepts
Understanding 25 divided by 2 serves as a springboard to exploring more complex mathematical concepts:
- Modular Arithmetic: The remainder (1 in this case) is crucial in modular arithmetic, where calculations are performed modulo a certain number (in this case, modulo 2).
- Algebra: Division is a fundamental operation in algebraic equations, used to solve for unknown variables.
- Calculus: The concept of division plays a role in differential calculus, particularly in finding derivatives and rates of change.
- Number Theory: Division and its properties are central to number theory, including topics like prime numbers and divisibility rules.
Frequently Asked Questions (FAQ)
Q1: What is the best way to calculate 25 divided by 2?
A1: The "best" method depends on your context and preference. Long division helps you understand the process, fractions provide a precise representation, and decimals offer ease of use in many applications.
Q2: What if I have a larger number to divide by 2?
A2: The same principles apply. You can use long division, fractions, or decimals. For very large numbers, a calculator or computer program is often the most efficient approach.
Q3: Why is understanding division important?
A3: Division is a fundamental mathematical operation crucial for solving problems in various contexts, from daily life to complex scientific calculations. A strong grasp of division builds a solid foundation for higher-level mathematics and problem-solving skills.
Q4: How do I handle remainders in division problems?
A4: You can express the remainder as a fraction (e.g., 1/2) or a decimal (e.g., 0.5) depending on the context. Understanding the meaning of the remainder in the given situation is key.
Q5: Are there any tricks or shortcuts for dividing by 2?
A5: Dividing by 2 is equivalent to multiplying by 0.5 or halving the number. This can be a quick way to solve the problem mentally for some numbers.
Conclusion: Mastering the Fundamentals
The seemingly straightforward calculation of 25 divided by 2 reveals a depth of mathematical principles and practical applications. This comprehensive exploration has not only provided the solution but also laid out the foundations for a deeper understanding of division, fractions, decimals, and their roles in various mathematical disciplines and real-world scenarios. By mastering the fundamental concept of division, you build a solid framework for tackling more complex mathematical challenges and applying these concepts effectively in your daily life and various academic or professional pursuits. Remember, a strong foundation in basic arithmetic, like understanding 25 divided by 2, is essential for unlocking advanced mathematical concepts and their numerous real-world applications.
Latest Posts
Latest Posts
-
What Is 2 3 Plus 2 3
Sep 18, 2025
-
How Long Is 7 Meters
Sep 18, 2025
-
Height Of A Triangular Prism
Sep 18, 2025
-
Gcf Of 56 And 21
Sep 18, 2025
-
How Old Is September 2006
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 5 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.