What Is 2/3 Plus 2/3
saludintensiva
Sep 18, 2025 · 5 min read
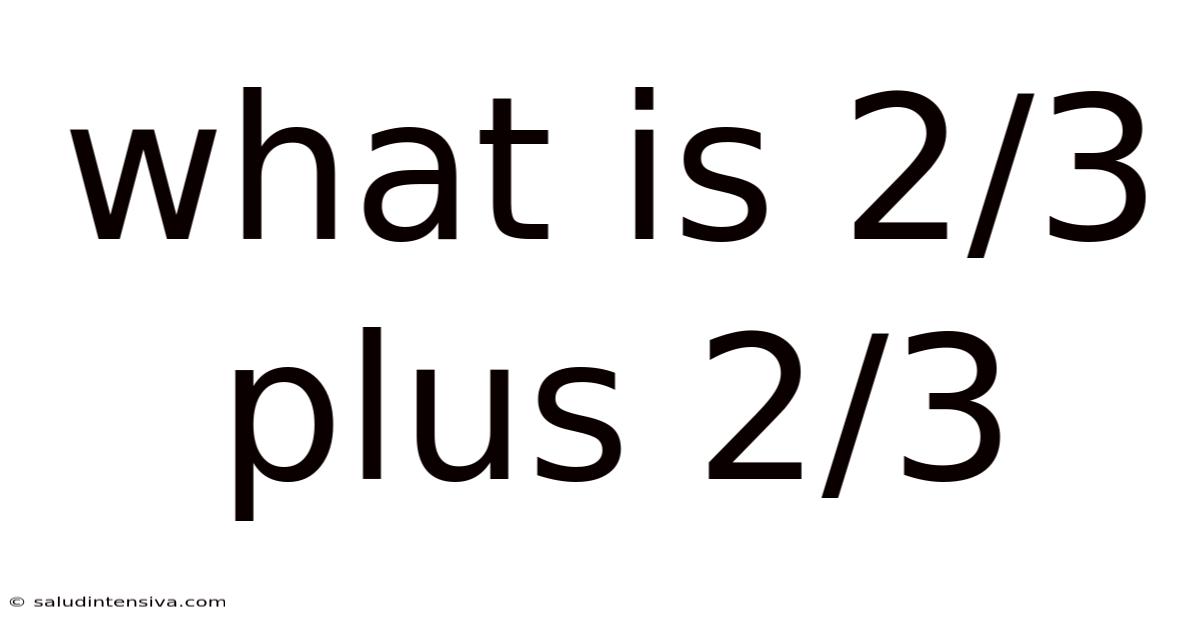
Table of Contents
What is 2/3 Plus 2/3? A Deep Dive into Fraction Addition
This article explores the seemingly simple question, "What is 2/3 plus 2/3?", but expands beyond the immediate answer to provide a comprehensive understanding of fraction addition, its applications, and related mathematical concepts. We'll cover the basic steps, delve into the underlying principles, and address common misconceptions, making this a valuable resource for anyone looking to solidify their understanding of fractions. Understanding fraction addition is crucial for various fields, from baking and cooking to engineering and finance.
Introduction: Understanding Fractions
Before tackling the problem, let's review the fundamentals of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 2/3, the denominator 3 means the whole is divided into three equal parts, and the numerator 2 means we are considering two of those parts.
Adding Fractions: The Basic Rule
The core principle of adding fractions with the same denominator is remarkably straightforward: add the numerators and keep the denominator the same. This makes perfect intuitive sense; if you have two parts out of three, and you add another two parts out of three, you end up with four parts out of three.
Therefore, 2/3 + 2/3 = (2 + 2) / 3 = 4/3
Solving 2/3 + 2/3: A Step-by-Step Approach
Let's break down the solution methodically:
-
Identify the denominators: Both fractions have a denominator of 3. This is crucial because it allows for direct addition of the numerators.
-
Add the numerators: Add the numerators together: 2 + 2 = 4.
-
Maintain the denominator: The denominator remains unchanged at 3.
-
Result: The sum is 4/3.
Improper Fractions and Mixed Numbers
The result, 4/3, is an improper fraction because the numerator (4) is larger than the denominator (3). Improper fractions are perfectly valid, but they are often converted to mixed numbers for easier interpretation. A mixed number combines a whole number and a proper fraction.
To convert 4/3 to a mixed number:
-
Divide the numerator by the denominator: 4 ÷ 3 = 1 with a remainder of 1.
-
Write the result: The quotient (1) becomes the whole number part, and the remainder (1) becomes the numerator of the fraction, while the denominator remains the same (3).
-
Final mixed number: 4/3 = 1 1/3
Therefore, 2/3 + 2/3 = 4/3 = 1 1/3
Visual Representation: Understanding the Concept
Visual aids are invaluable for grasping fractional concepts. Imagine a pizza cut into three equal slices. 2/3 represents two slices of the pizza. Adding another 2/3 means adding two more slices. In total, you have four slices, which is more than one whole pizza. This visually confirms that 2/3 + 2/3 = 4/3 or 1 1/3. You have one whole pizza and one-third of another.
Adding Fractions with Different Denominators
While the example above dealt with fractions having the same denominator, adding fractions with different denominators requires an extra step: finding a common denominator. A common denominator is a number that is a multiple of both denominators.
For instance, let's consider 1/2 + 1/4. The common denominator is 4 (because 4 is a multiple of both 2 and 4). We convert 1/2 to an equivalent fraction with a denominator of 4: 1/2 = 2/4. Then, we add: 2/4 + 1/4 = 3/4.
This process of finding the least common denominator (LCD) is crucial for accurate fraction addition. The LCD is the smallest common multiple of the denominators. Finding the LCD often involves prime factorization or identifying common multiples.
Real-World Applications of Fraction Addition
The ability to add fractions is surprisingly applicable in everyday life and various professions:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. Adding fractions helps accurately determine the total amount of an ingredient needed. For example, if a recipe calls for 1/2 cup of flour and 1/4 cup of sugar, you'd add the fractions to find the total amount of dry ingredients.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Adding fractional measurements ensures accurate calculations for building materials and structural components.
-
Finance: Managing budgets and calculating financial ratios often involves working with fractions and percentages, which are closely related to fractions.
-
Data Analysis: In statistics and data analysis, dealing with proportions and ratios involves a strong understanding of fractions and fractional arithmetic.
Frequently Asked Questions (FAQs)
Q1: What if I get a negative fraction?
A1: The same rules apply. You add the numerators, keeping the sign of the numerator and the denominator the same. For example, -2/3 + (-1/3) = -3/3 = -1.
Q2: Can I add fractions using a calculator?
A2: Yes, most calculators have the functionality to add fractions directly. Some calculators might require you to input the fractions as decimals first.
Q3: Why is it important to simplify fractions?
A3: Simplifying fractions (reducing them to their lowest terms) makes them easier to understand and work with. It presents the fraction in its most concise form. For example, 4/6 simplifies to 2/3.
Q4: What if the fractions have different denominators and finding the LCD is challenging?
A4: While finding the least common denominator (LCD) is ideal, any common denominator will work. You can always multiply the denominators to find a common denominator, though it might lead to larger numbers and a need for simplification later.
Conclusion: Mastering Fraction Addition
This exploration of "What is 2/3 plus 2/3?" has expanded into a broader understanding of fraction addition, its foundational principles, and practical applications. While the initial answer is straightforward (4/3 or 1 1/3), the underlying concepts are essential for various mathematical and real-world situations. Mastering fraction addition is a stepping stone to more advanced mathematical concepts and crucial for problem-solving in numerous fields. By understanding the basic rules and practicing regularly, you'll build confidence and proficiency in working with fractions. Remember that the key lies not just in getting the right answer but in understanding why the answer is correct. This conceptual understanding fosters a deeper appreciation for the elegance and power of mathematics.
Latest Posts
Latest Posts
-
Is 5 16 Bigger Than 1 4
Sep 18, 2025
-
1 2 2 1 3
Sep 18, 2025
-
Gcf Of 75 And 15
Sep 18, 2025
-
Whats 1330 In Military Time
Sep 18, 2025
-
Equation To Standard Form Calculator
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Plus 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.