Is 5/16 Bigger Than 1/4
saludintensiva
Sep 18, 2025 · 5 min read
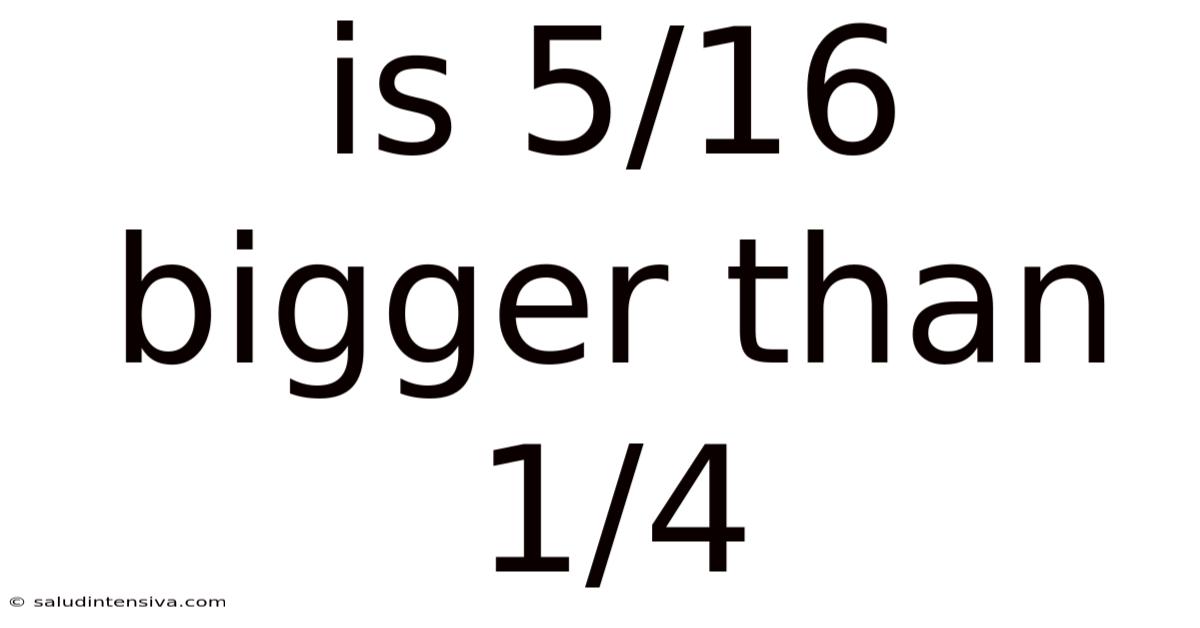
Table of Contents
Is 5/16 Bigger Than 1/4? A Deep Dive into Fraction Comparison
Many of us encounter fraction comparisons in our daily lives, from baking recipes to understanding data. Knowing how to compare fractions is a crucial skill, and a common question that arises is: is 5/16 bigger than 1/4? This article will not only answer this question definitively but will also equip you with the tools and understanding to compare any two fractions confidently. We'll explore various methods, delve into the underlying mathematical principles, and even touch upon real-world applications to solidify your understanding.
Understanding Fractions: A Quick Refresher
Before we tackle the comparison, let's ensure we're all on the same page about fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) which indicates the number of parts we have, and the denominator (the bottom number) which indicates the total number of equal parts the whole is divided into. For instance, in the fraction 1/4, 1 is the numerator and 4 is the denominator, meaning we have 1 out of 4 equal parts.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The key idea is to rewrite both fractions so they share the same denominator. We do this by finding the least common multiple (LCM) of the denominators.
Let's compare 5/16 and 1/4. The denominators are 16 and 4. The LCM of 16 and 4 is 16 (because 16 is a multiple of 4).
- We leave 5/16 as it is, since its denominator is already 16.
- To convert 1/4 to have a denominator of 16, we multiply both the numerator and the denominator by 4: (1 × 4) / (4 × 4) = 4/16
Now we can easily compare: 5/16 and 4/16. Since 5 > 4, we conclude that 5/16 is bigger than 1/4.
Method 2: Converting to Decimals
Another effective method involves converting both fractions into decimals. To do this, we simply divide the numerator by the denominator.
- 5/16 = 0.3125
- 1/4 = 0.25
Comparing the decimal values, 0.3125 > 0.25, confirming that 5/16 is bigger than 1/4. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
Method 3: Visual Representation
While less suitable for complex fractions, a visual approach can be highly effective for building intuition, especially for beginners. Imagine a pizza cut into 16 slices (representing 16ths) and another pizza cut into 4 slices (representing quarters).
- In the first pizza, 5/16 means you have 5 out of 16 slices.
- In the second pizza, 1/4 means you have 1 out of 4 slices. Since 1/4 of the pizza is equivalent to 4/16 of the pizza (as we established earlier), it's clear that 5/16 represents a larger portion of the pizza.
The Mathematical Rationale Behind Fraction Comparison
The methods above all rely on the fundamental principle of representing fractions as equivalent parts of a whole. By finding a common denominator or converting to decimals, we're essentially standardizing the units of measurement, making direct comparison possible. The fraction with the larger numerator (when the denominators are the same) represents the larger portion of the whole.
Beyond the Basics: Extending Fraction Comparison Skills
The techniques discussed above can be applied to compare any two fractions, regardless of their complexity. Here’s how to approach more challenging scenarios:
- Fractions with different denominators: Always start by finding the LCM of the denominators. If the LCM is difficult to find, consider using prime factorization to simplify the process.
- Improper fractions (numerator > denominator): These fractions represent values greater than 1. Convert them to mixed numbers (whole number and a fraction) for easier comparison. For example, 7/4 = 1 ¾.
- Comparing more than two fractions: Follow the same principles. Find a common denominator for all fractions and then compare their numerators.
Real-World Applications of Fraction Comparison
Understanding fraction comparison is crucial in various real-world applications:
- Cooking and Baking: Recipes often involve fractions. Accurately comparing fractions ensures the correct proportions of ingredients.
- Construction and Engineering: Precise measurements and calculations often rely on fractions, especially when working with inches or millimeters.
- Finance: Understanding fractions is essential for working with percentages, interest rates, and proportions of investments.
- Data Analysis: Many data sets involve fractions or proportions, requiring accurate comparison to draw meaningful conclusions.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to compare fractions?
A1: The easiest way depends on your comfort level and the specific fractions. Finding a common denominator is generally straightforward and reliable. Converting to decimals can be quicker for some fractions, especially those with larger denominators.
Q2: Can I always find a common denominator?
A2: Yes, you can always find a common denominator for any two (or more) fractions. The least common multiple (LCM) of the denominators will always serve as a common denominator.
Q3: What if the fractions are very large and complex?
A3: For very large and complex fractions, converting to decimals is often the more efficient approach. You can use a calculator to perform the divisions accurately.
Q4: Are there any online tools or calculators that can help with fraction comparison?
A4: While this article doesn't include links to external resources, numerous online calculators and tools are available to aid in fraction comparison and other mathematical calculations. Searching for "fraction calculator" on a search engine will yield many results.
Conclusion: Mastering Fraction Comparison
The question "Is 5/16 bigger than 1/4?" is a stepping stone to mastering fraction comparison. We've explored multiple methods – finding a common denominator, converting to decimals, and visual representation – each providing a different perspective on this fundamental mathematical concept. By understanding these methods and their underlying principles, you'll be well-equipped to tackle any fraction comparison confidently. Remember, practice is key. The more you work with fractions, the more intuitive the process will become, enabling you to solve problems quickly and accurately in various contexts. So, keep practicing and enjoy the journey of mastering fractions!
Latest Posts
Latest Posts
-
16 20 In Simplest Form
Sep 18, 2025
-
What Is Half Of 43
Sep 18, 2025
-
How To Find A Dimension
Sep 18, 2025
-
Is 1 2 Greater Than 1 6
Sep 18, 2025
-
How Much Is 50 Kg
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 5/16 Bigger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.