2 Divided By 1 3
saludintensiva
Sep 16, 2025 · 5 min read
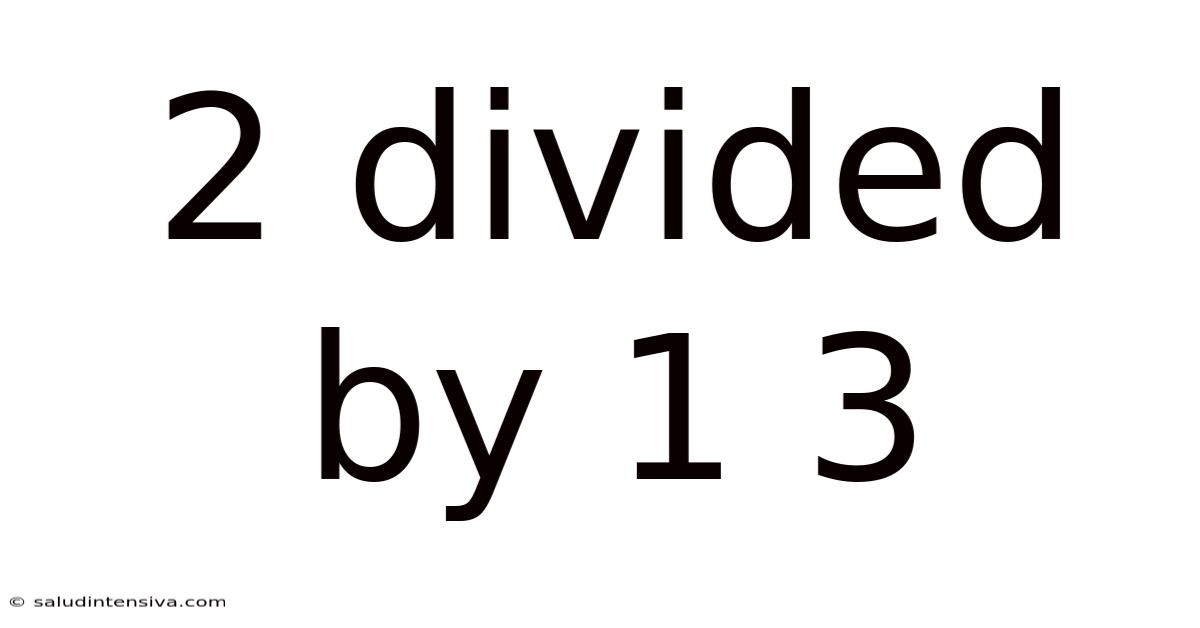
Table of Contents
Unveiling the Mystery: A Deep Dive into 2 Divided by 1/3
Understanding division, especially when fractions are involved, can sometimes feel like navigating a mathematical maze. This article will illuminate the process of dividing 2 by 1/3, providing a step-by-step guide, explaining the underlying principles, and addressing common misconceptions. We'll explore various methods, ensuring a clear and comprehensive understanding for learners of all levels. By the end, you'll not only know the answer but also grasp the why behind the calculation, empowering you to tackle similar problems with confidence.
Understanding the Problem: 2 ÷ 1/3
The problem "2 divided by 1/3" (or 2 ÷ 1/3) asks: how many times does 1/3 fit into 2? This seemingly simple question often trips up students because it involves dividing by a fraction, a concept that requires a solid understanding of fractional arithmetic. Let's break down the process using several approaches.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is arguably the most common and straightforward method for dividing fractions. It's based on the principle that dividing by a fraction is the same as multiplying by its reciprocal.
- Step 1: Keep the first number: We keep the number 2 as it is.
- Step 2: Change the division sign: We change the division symbol (÷) to a multiplication symbol (×).
- Step 3: Flip the second number (find the reciprocal): The reciprocal of 1/3 is 3/1 (or simply 3). This is because multiplying a fraction by its reciprocal always equals 1 (1/3 x 3/1 = 1).
Therefore, the problem becomes: 2 × 3
- Step 4: Perform the multiplication: 2 × 3 = 6
Therefore, 2 ÷ 1/3 = 6
Method 2: Visual Representation with Fraction Bars
This method offers a visual approach, enhancing understanding, especially for visual learners.
Imagine you have two whole bars representing the number 2. Each bar is divided into thirds.
[Visual representation would be included here if this were a document with image capabilities. Imagine two bars divided into three equal sections each. This would visually represent the six thirds in total.]
Each of those sections represents 1/3. By counting the total number of thirds in the two bars, we clearly see there are six sections of 1/3. This provides a visual confirmation that 2 ÷ 1/3 = 6.
Method 3: Using the Definition of Division
Division can be defined as the inverse operation of multiplication. This means that if a ÷ b = c, then c × b = a. Let's apply this to our problem:
Let's assume that 2 ÷ 1/3 = x. According to the definition of division, this means:
x × (1/3) = 2
To solve for x, we multiply both sides by 3 (the reciprocal of 1/3):
x × (1/3) × 3 = 2 × 3
x = 6
This reinforces our previous findings, demonstrating that 2 ÷ 1/3 = 6.
Method 4: Converting to Improper Fractions
Another approach involves converting the whole number (2) into a fraction. Remember, any whole number can be written as a fraction with a denominator of 1. Thus, 2 can be written as 2/1.
The problem then becomes: (2/1) ÷ (1/3)
Now, we apply the "keep, change, flip" method:
(2/1) × (3/1) = 6/1 = 6
Again, this method leads us to the same answer: 6.
Addressing Common Misconceptions
Many students struggle with dividing by fractions, often making the mistake of simply dividing the numerators and the denominators. This is incorrect. Division with fractions requires understanding the concept of reciprocals and the relationship between division and multiplication.
The Significance of Reciprocals
The core concept underpinning division by fractions is the use of reciprocals. A reciprocal of a number is simply 1 divided by that number. For example:
- The reciprocal of 5 is 1/5.
- The reciprocal of 2/3 is 3/2.
- The reciprocal of 1/3 is 3.
Understanding reciprocals is crucial for mastering division involving fractions.
Expanding the Concept: Beyond 2 ÷ 1/3
The principles we've explored aren't limited to this specific problem. They apply to any division involving fractions. For example, consider 5 ÷ 2/7:
- Keep: 5
- Change: ÷ to ×
- Flip: 2/7 becomes 7/2
- Multiply: 5 × 7/2 = 35/2 = 17.5
This demonstrates the versatility of the "keep, change, flip" method.
Practical Applications
Understanding division with fractions is essential in various real-world scenarios. Imagine you have 2 yards of fabric and need to cut pieces that are 1/3 of a yard long. How many pieces can you cut? The answer, as we've established, is 6.
Frequently Asked Questions (FAQ)
-
Q: Why does the "keep, change, flip" method work? A: It works because dividing by a fraction is equivalent to multiplying by its reciprocal. This is a fundamental property of fractions and their inverse operations.
-
Q: Can I use a calculator to solve this? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for solving more complex problems and building a strong mathematical foundation.
-
Q: What if I have to divide a fraction by another fraction? A: The same "keep, change, flip" method applies. For example, (1/2) ÷ (1/4) becomes (1/2) × (4/1) = 2.
-
Q: Is there a different way to understand why 2 divided by 1/3 equals 6? A: Yes, consider that you have two items and you want to divide each item into thirds. That means you have a total of 2 x 3 = 6 thirds.
Conclusion
Dividing 2 by 1/3 reveals a fundamental concept in mathematics: the relationship between division and multiplication, particularly with fractions. By employing the "keep, change, flip" method, or visualizing the problem through fraction bars, the solution becomes clear. Mastering these techniques will empower you to confidently solve similar problems and build a strong foundation in fractions and their operations, setting you up for success in more advanced mathematical concepts. Remember, the key is not just knowing the answer (6), but understanding the why behind the calculation. This understanding is the cornerstone of true mathematical proficiency.
Latest Posts
Latest Posts
-
What Is 3 10 Of 150
Sep 16, 2025
-
10 6 As A Fraction
Sep 16, 2025
-
10 30 As A Percent
Sep 16, 2025
-
10 To The Power 11
Sep 16, 2025
-
3 4 As A Whole Number
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.