2 Divided By Negative 2
saludintensiva
Sep 10, 2025 · 5 min read
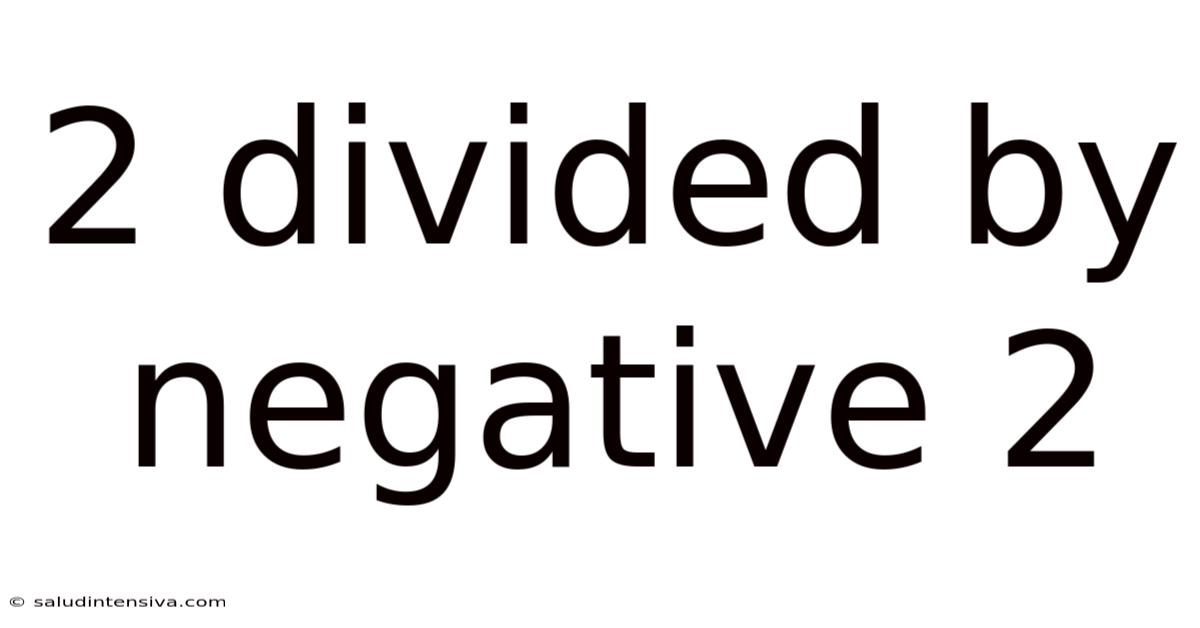
Table of Contents
Unveiling the Mystery: 2 Divided by -2
This seemingly simple arithmetic problem, 2 divided by -2 (or 2/-2), often trips up students transitioning from basic arithmetic to more advanced mathematical concepts. Understanding this seemingly basic calculation isn't just about getting the right answer; it's about grasping the fundamental principles of division and negative numbers, which are building blocks for more complex mathematical operations and concepts in algebra, calculus, and beyond. This comprehensive guide will explore the solution, delve into the underlying mathematical principles, address common misconceptions, and provide a solid foundation for understanding similar problems.
Understanding Division: A Foundational Review
Before tackling the specific problem, let's refresh our understanding of division. Division is essentially the inverse operation of multiplication. When we say "2 divided by -2," we're asking: "What number, when multiplied by -2, equals 2?" This framing helps clarify the process and connect division with its multiplicative counterpart. Thinking in this way will be incredibly helpful when we deal with negative numbers.
Consider a simpler example: 6 divided by 2. We can express this as 6/2 = 3. This means that 2 multiplied by 3 equals 6. The same logic applies to our problem: 2/-2. We are seeking the number that, when multiplied by -2, results in 2.
Solving 2 Divided by -2: The Mechanics
Now, let's address the specific problem: 2/-2. Using the principle discussed above, we ask: what number multiplied by -2 gives us 2? The answer is -1.
Therefore:
2 / -2 = -1
This seemingly straightforward answer hides a crucial concept: the rules governing the division of positive and negative numbers.
The Rules of Signs in Division (and Multiplication)
The key to understanding the solution lies in the rules of signs for multiplication and division, which are intimately linked:
-
Positive ÷ Positive = Positive: A positive number divided by a positive number always results in a positive number. For example, 10 / 2 = 5.
-
Positive ÷ Negative = Negative: A positive number divided by a negative number always results in a negative number. This is the crucial rule for understanding our problem: 2 / -2 = -1.
-
Negative ÷ Positive = Negative: A negative number divided by a positive number always results in a negative number. For example, -10 / 2 = -5.
-
Negative ÷ Negative = Positive: A negative number divided by a negative number always results in a positive number. For example, -10 / -2 = 5.
These rules stem from the properties of multiplication and the inverse relationship between multiplication and division. Remember that division is essentially repeated subtraction, and multiplication is repeated addition. Understanding the interplay between addition and subtraction of positive and negative numbers is crucial here.
Visualizing the Problem: The Number Line
The number line is a powerful tool for visualizing operations with negative numbers. Imagine the number line with 0 at the center, positive numbers to the right, and negative numbers to the left. Division can be visualized as partitioning. If we divide 2 by -2, we are essentially splitting 2 into two equal parts, but moving in the negative direction. This leads us to -1 on the number line.
Expanding the Understanding: Fractions and Equivalent Expressions
Our problem can also be represented as a fraction: 2/-2. Remember that fractions represent division. We can simplify this fraction by dividing both the numerator (2) and the denominator (-2) by their greatest common divisor (GCD), which is 2. This gives us:
2/-2 = (2/2) / (-2/2) = 1/-1 = -1
This approach reinforces the concept of equivalent fractions and demonstrates another way to arrive at the correct answer.
Common Misconceptions and Pitfalls
Students often struggle with the rules of signs, particularly when dealing with negative numbers. Some common misconceptions include:
-
Ignoring the negative sign: Failing to consider the negative sign in the denominator is a frequent error. Remember that the negative sign is integral to the operation and impacts the sign of the result.
-
Confusing addition/subtraction rules with division/multiplication rules: Students sometimes apply the rules for addition and subtraction to division and multiplication, leading to incorrect answers. The rules are distinct for each operation.
-
Overlooking simplification: Failing to simplify fractions can lead to more complex calculations and increase the chances of error.
Further Exploration: Real-World Applications
While 2 / -2 might seem abstract, understanding the rules of signs has far-reaching implications in various real-world applications:
-
Finance: Profit and loss calculations often involve negative numbers, representing losses. Understanding division with negative numbers is crucial for interpreting financial statements and making informed decisions.
-
Physics: Many physics equations involve negative values to represent direction or opposing forces. Mastering these rules is essential for solving problems in mechanics, electricity, and other branches of physics.
-
Computer Science: Negative numbers are fundamental to computer programming and data representation. Understanding the rules of sign is necessary for writing accurate and efficient code.
Frequently Asked Questions (FAQs)
Q: What if the problem were -2 divided by 2?
A: Following the same principle, -2 / 2 = -1. A negative number divided by a positive number results in a negative number.
Q: What about 0 divided by -2?
A: 0 divided by any non-zero number is always 0. So, 0 / -2 = 0.
Q: What about -2 divided by 0?
A: Division by zero is undefined in mathematics. It's a concept that leads to inconsistencies and paradoxes within the mathematical framework.
Q: Is there a difference between 2/-2 and -2/2?
A: No, both expressions represent the same division problem and will result in the same answer, -1.
Conclusion: Mastering the Fundamentals
Understanding 2 divided by -2 is more than just finding the answer (-1). It's about solidifying a grasp on the fundamental principles of division, the rules of signs, and their application in various contexts. By understanding these concepts, you'll build a strong foundation for more advanced mathematical studies and real-world problem-solving. Remember to practice regularly, visualize using the number line, and always double-check your work to reinforce your understanding of these essential mathematical rules. This seemingly simple equation opens the door to a deeper comprehension of the elegance and logic inherent in mathematical operations.
Latest Posts
Latest Posts
-
Lcm Of 20 And 24
Sep 10, 2025
-
What Is 2 3 2 3
Sep 10, 2025
-
Illinois Sales Tax Rate Lookup
Sep 10, 2025
-
31 Degree Fahrenheit To Celsius
Sep 10, 2025
-
Convert 21 C To Fahrenheit
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 2 Divided By Negative 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.