21/16 As A Mixed Number
saludintensiva
Sep 19, 2025 · 6 min read
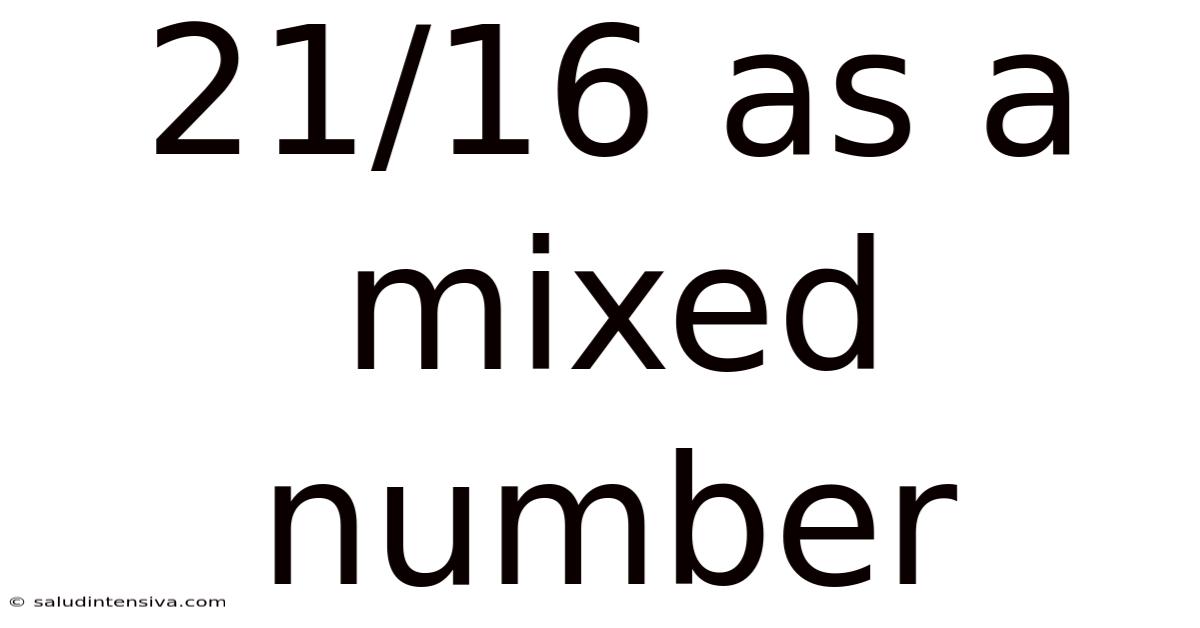
Table of Contents
Understanding 21/16 as a Mixed Number: A Comprehensive Guide
The seemingly simple fraction 21/16 presents a great opportunity to delve into the world of mixed numbers, a crucial concept in arithmetic and a stepping stone to more advanced mathematical concepts. This comprehensive guide will not only show you how to convert 21/16 into a mixed number but also explore the underlying principles, provide practical examples, and address frequently asked questions. Understanding mixed numbers is essential for various applications, from baking recipes to engineering calculations. Let's embark on this mathematical journey together!
What is a Mixed Number?
Before tackling the conversion of 21/16, let's establish a solid understanding of what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity that is more than one whole unit but less than the next whole number.
Converting an Improper Fraction to a Mixed Number
The fraction 21/16 is an improper fraction. An improper fraction is one where the numerator is greater than or equal to the denominator. To convert an improper fraction into a mixed number, we need to perform a simple division. Here’s how:
1. Divide the Numerator by the Denominator:
Divide the numerator (21) by the denominator (16).
21 ÷ 16 = 1 with a remainder of 5
2. Identify the Whole Number:
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
3. Determine the Fractional Part:
The remainder (5) becomes the numerator of the fractional part, while the denominator remains the same (16). Therefore, the fractional part is 5/16.
4. Combine the Whole Number and Fractional Part:
Combine the whole number and the fractional part to form the mixed number. So, 21/16 as a mixed number is 1 5/16.
Visualizing the Conversion: A Practical Example
Imagine you have 21 slices of pizza, and each pizza has 16 slices. You can clearly see that you have more than one whole pizza.
- You can make one complete pizza using 16 slices (leaving 5 slices).
- You have one whole pizza (1) and 5 slices remaining out of the 16 slices needed for another whole pizza (5/16).
Therefore, you have 1 5/16 pizzas. This visual representation makes the concept of mixed numbers more concrete and easier to grasp.
The Importance of Understanding Mixed Numbers
The ability to convert between improper fractions and mixed numbers is fundamental to various mathematical operations and real-world applications. Here are some examples:
-
Measurement: Imagine measuring the length of a piece of wood. If the measurement is 21/16 inches, expressing it as 1 5/16 inches is often more intuitive and practical.
-
Cooking and Baking: Recipes frequently use mixed numbers to represent quantities of ingredients. Understanding mixed numbers ensures accurate ingredient measurements.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Converting between fractions and mixed numbers ensures accurate calculations and avoids potential errors.
-
Advanced Mathematics: Converting between improper fractions and mixed numbers is a crucial skill that forms the foundation for more advanced mathematical concepts, such as algebraic manipulations and calculus.
Further Exploration: Working with Mixed Numbers
Now that we've successfully converted 21/16 to a mixed number, let's explore further operations involving mixed numbers:
-
Adding Mixed Numbers: To add mixed numbers, you can either convert them to improper fractions first and then add, or add the whole numbers separately and the fractions separately, then simplify the result.
-
Subtracting Mixed Numbers: Similar to addition, you can either convert to improper fractions first or subtract the whole numbers and fractions separately, borrowing if necessary.
-
Multiplying Mixed Numbers: It's generally easier to convert mixed numbers to improper fractions before multiplying.
-
Dividing Mixed Numbers: Again, converting mixed numbers to improper fractions simplifies the division process.
Step-by-Step Guide to Operations with Mixed Numbers
Let's illustrate with some examples:
1. Addition:
Add 1 5/16 and 2 3/8.
- Convert to improper fractions: 1 5/16 = 21/16 and 2 3/8 = 19/8
- Find a common denominator: The common denominator for 16 and 8 is 16.
- Convert fractions to common denominator: 19/8 = 38/16
- Add the fractions: 21/16 + 38/16 = 59/16
- Convert back to a mixed number: 59/16 = 3 11/16
2. Subtraction:
Subtract 1 5/16 from 3 1/4.
- Convert to improper fractions: 3 1/4 = 13/4 and 1 5/16 = 21/16
- Find a common denominator: The common denominator for 4 and 16 is 16.
- Convert fractions to common denominator: 13/4 = 52/16
- Subtract the fractions: 52/16 - 21/16 = 31/16
- Convert back to a mixed number: 31/16 = 1 15/16
3. Multiplication:
Multiply 1 5/16 by 2 1/2.
- Convert to improper fractions: 1 5/16 = 21/16 and 2 1/2 = 5/2
- Multiply the numerators and denominators: (21 x 5) / (16 x 2) = 105/32
- Convert back to a mixed number: 105/32 = 3 9/32
4. Division:
Divide 3 1/4 by 1 5/16.
- Convert to improper fractions: 3 1/4 = 13/4 and 1 5/16 = 21/16
- Invert the second fraction and multiply: (13/4) x (16/21) = 52/21
- Convert back to a mixed number: 52/21 = 2 10/21
Frequently Asked Questions (FAQs)
Q1: Why is it important to learn about mixed numbers?
A1: Mixed numbers are essential for practical applications in various fields, including cooking, construction, engineering, and more advanced mathematics. They provide a more intuitive and user-friendly way to represent quantities that are more than one whole unit.
Q2: Can I always convert an improper fraction into a mixed number?
A2: Yes, any improper fraction can always be converted into a mixed number, provided the denominator is not zero.
Q3: What if the remainder is zero after dividing the numerator by the denominator?
A3: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 16/16 = 1.
Q4: Is there a shortcut to converting an improper fraction to a mixed number?
A4: While the long division method is clear and understandable, with practice, you might develop an intuitive sense for converting some improper fractions quickly.
Conclusion
Converting 21/16 to the mixed number 1 5/16 is a straightforward process involving simple division. Understanding this concept is crucial for various mathematical operations and practical applications. Mastering the conversion between improper fractions and mixed numbers is a fundamental skill that lays the foundation for more advanced mathematical concepts and real-world problem-solving. By practicing these conversions and exploring the various operations with mixed numbers, you'll build a strong foundation in arithmetic and enhance your mathematical proficiency. Remember, practice makes perfect! Keep working with fractions and mixed numbers, and you'll soon find yourself confidently navigating the world of numbers.
Latest Posts
Latest Posts
-
What Is Half Of 19
Sep 19, 2025
-
Rounding To The Greatest Place
Sep 19, 2025
-
Is 2 5 Greater Than 3 8
Sep 19, 2025
-
Year Of Birth Age Chart
Sep 19, 2025
-
Specific Mass Conversions Quick Check
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 21/16 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.