23/4 As A Mixed Number
saludintensiva
Sep 18, 2025 · 5 min read
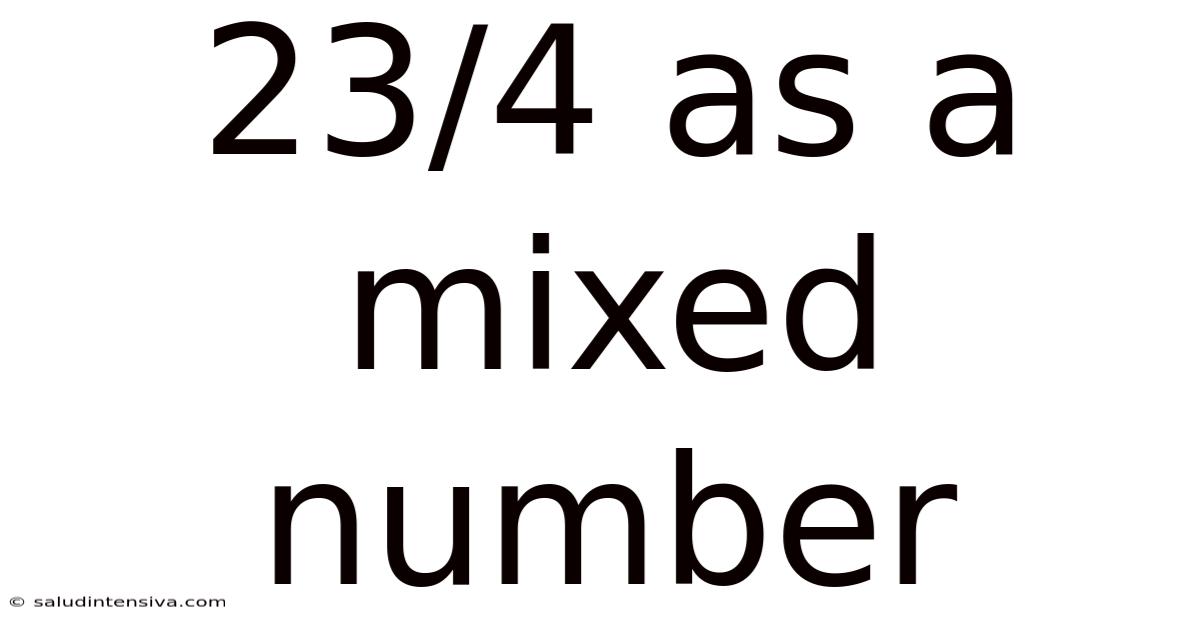
Table of Contents
Understanding 23/4 as a Mixed Number: A Comprehensive Guide
The fraction 23/4 represents a value greater than one whole. Understanding how to convert improper fractions, like 23/4, into mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 23/4 to a mixed number but also delve into the underlying principles, provide practical examples, and explore related concepts. We'll also address frequently asked questions to ensure a complete understanding.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent values greater than one but less than the next whole number.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 23/4 is an improper fraction because 23 (numerator) is greater than 4 (denominator). To convert an improper fraction to a mixed number, we need to determine how many whole numbers are contained within the fraction and the remaining fractional part.
Steps to Convert 23/4 to a Mixed Number
Here's a step-by-step process to convert 23/4 into its mixed number equivalent:
-
Division: Divide the numerator (23) by the denominator (4). 23 ÷ 4 = 5 with a remainder of 3.
-
Whole Number: The quotient (5) becomes the whole number part of the mixed number.
-
Fractional Part: The remainder (3) becomes the numerator of the fractional part, and the denominator remains the same (4).
-
Mixed Number: Combine the whole number and the fraction to form the mixed number: 5 ¾
Therefore, 23/4 expressed as a mixed number is 5 ¾.
Visual Representation
Imagine you have 23 quarters. Since four quarters make one dollar, you can group these quarters into sets of four. You'll have five complete sets (5 dollars) with three quarters remaining. This visually represents the conversion of 23/4 to 5 ¾.
Working with Other Improper Fractions
Let's apply the same method to a few more examples:
- 17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 ⅖.
- 29/8: 29 ÷ 8 = 3 with a remainder of 5. Therefore, 29/8 = 3 ⅝.
- 11/3: 11 ÷ 3 = 3 with a remainder of 2. Therefore, 11/3 = 3 ⅔.
These examples illustrate the consistent process of dividing the numerator by the denominator to obtain the whole number and the remaining fraction.
Converting Mixed Numbers back to Improper Fractions
It's also crucial to understand the reverse process: converting a mixed number back into an improper fraction. This is often necessary when performing calculations with mixed numbers.
The steps are:
- Multiply: Multiply the whole number by the denominator.
- Add: Add the result to the numerator.
- Fraction: Keep the same denominator.
Let's convert 5 ¾ back to an improper fraction:
- Multiply: 5 x 4 = 20
- Add: 20 + 3 = 23
- Fraction: 23/4
This confirms that our initial conversion was correct.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in various real-world scenarios:
- Measurement: Measuring lengths, weights, or volumes often involves mixed numbers. For example, a piece of wood might measure 2 ⅛ feet long.
- Cooking: Recipes often use mixed numbers to specify ingredient quantities, such as 1 ½ cups of flour.
- Time: We express time using mixed numbers, like 2 ½ hours.
The Importance of Understanding Fractions
A strong grasp of fractions is vital for success in mathematics and its applications. Understanding improper fractions and their conversion to mixed numbers is a cornerstone of this understanding. It's a skill that builds upon itself, forming the foundation for more advanced mathematical concepts such as algebra and calculus.
Why is this Conversion Important?
Converting between improper fractions and mixed numbers is crucial for several reasons:
- Simplicity: Mixed numbers are often easier to visualize and understand than improper fractions, particularly in real-world contexts.
- Calculations: While some calculations can be done with improper fractions, others are simplified significantly when using mixed numbers.
- Problem Solving: Many word problems necessitate converting between these two forms to solve them effectively.
Frequently Asked Questions (FAQ)
Q: What if the remainder is zero after dividing the numerator by the denominator?
A: If the remainder is zero, the improper fraction is already a whole number. For example, 12/4 = 3. There is no fractional part.
Q: Can I convert a mixed number into a decimal?
A: Yes, you can. First, convert the mixed number to an improper fraction and then divide the numerator by the denominator. For example, 5 ¾ becomes 23/4, which is 5.75 when converted to a decimal.
Q: Are there different methods for converting improper fractions to mixed numbers?
A: While the division method is the most common and straightforward, other methods exist, but they often rely on the same underlying principle of determining the whole number and the remaining fractional part.
Q: What if I have a negative improper fraction?
A: The process remains the same, but the resulting mixed number will also be negative. For example, -23/4 = -5 ¾.
Conclusion
Mastering the conversion between improper fractions and mixed numbers is a crucial skill in mathematics. This guide has provided a comprehensive understanding of this process, illustrating the steps involved, offering visual representations, and exploring practical applications. By understanding the underlying principles and practicing the conversion process, you'll build a strong foundation for more advanced mathematical concepts and real-world problem-solving. Remember, consistent practice is key to mastering this important arithmetic skill. The ability to seamlessly move between improper fractions and mixed numbers will greatly enhance your mathematical proficiency and problem-solving abilities.
Latest Posts
Latest Posts
-
2 5 Divided By 2
Sep 18, 2025
-
4 Thousandths As A Decimal
Sep 18, 2025
-
What Is This Number Pronounces
Sep 18, 2025
-
Greatest Common Factor Of 100
Sep 18, 2025
-
1 2 As An Improper Fraction
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 23/4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.