23/9 As A Mixed Number
saludintensiva
Sep 18, 2025 · 5 min read
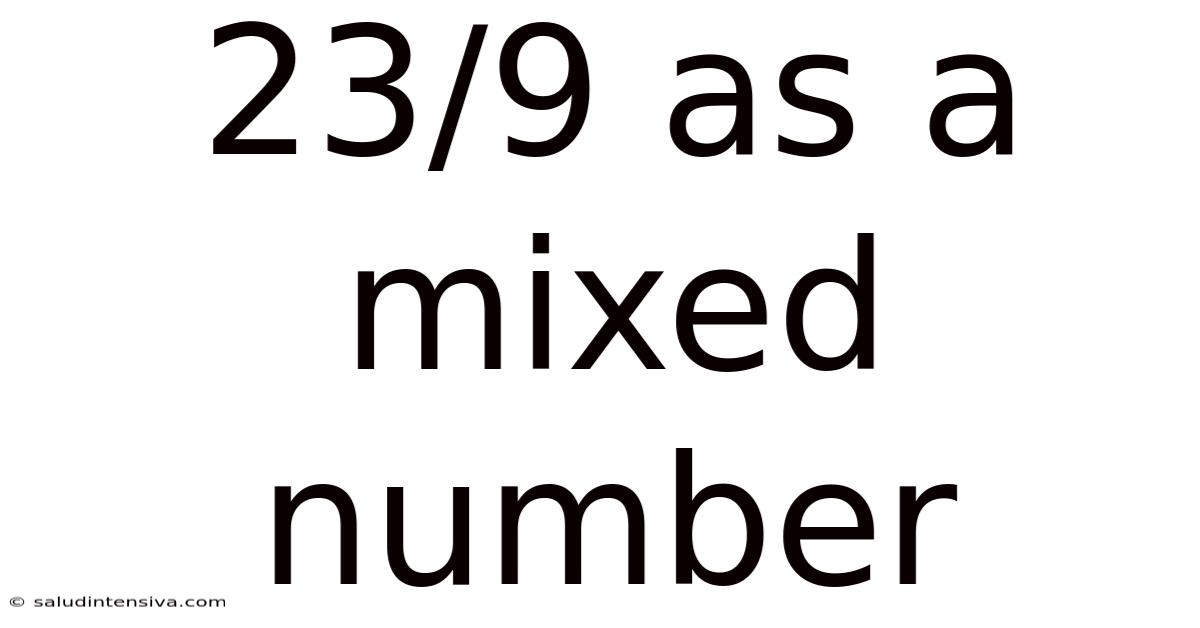
Table of Contents
Understanding 23/9 as a Mixed Number: A Comprehensive Guide
The fraction 23/9 represents a quantity greater than one whole. Understanding how to express this improper fraction as a mixed number is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 23/9 into a mixed number but also delve into the underlying principles, provide practical examples, and address common questions. We'll explore the concept thoroughly, making it easy to understand for students of all levels.
Introduction: What are Improper Fractions and Mixed Numbers?
Before we dive into converting 23/9, let's clarify some terminology. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 11/5, and, of course, 23/9. These fractions represent values larger than one.
A mixed number, on the other hand, combines a whole number and a proper fraction. A proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4, 2/5). Mixed numbers provide a more intuitive way to represent quantities larger than one. For instance, 2 1/2 is a mixed number representing two whole units and an additional half.
Converting 23/9 to a Mixed Number: A Step-by-Step Approach
Converting an improper fraction like 23/9 to a mixed number involves a simple division process. Here's the step-by-step method:
-
Divide the numerator by the denominator: Divide 23 by 9. This gives us a quotient and a remainder.
23 ÷ 9 = 2 with a remainder of 5
-
The quotient becomes the whole number part: The quotient, 2, represents the number of whole units contained within the fraction.
-
The remainder becomes the numerator of the fraction part: The remainder, 5, becomes the numerator of the new fraction.
-
The denominator remains the same: The denominator of the mixed number is the same as the denominator of the original improper fraction, which is 9.
Therefore, 23/9 as a mixed number is 2 5/9.
Visualizing the Conversion: A Concrete Example
Imagine you have 23 identical cookies, and you want to divide them equally among 9 friends. You can give each friend 2 cookies (that's 2 x 9 = 18 cookies). You'll have 5 cookies left over (23 - 18 = 5). So each friend gets 2 whole cookies, and you have 5/9 of a cookie remaining. This visually represents the conversion of 23/9 to 2 5/9.
The Mathematical Explanation: Understanding the Process
The conversion from an improper fraction to a mixed number is based on the fundamental concept of division. We are essentially dividing the larger quantity (the numerator) into equal parts represented by the denominator. The whole number part represents the number of times the denominator completely divides into the numerator, while the fraction part represents the remaining portion.
Formally, we can express this as:
Improper Fraction = (Quotient x Denominator) + Remainder / Denominator = Quotient + Remainder/Denominator
In the case of 23/9:
23/9 = (2 x 9) + 5 / 9 = 2 + 5/9 = 2 5/9
Converting Mixed Numbers back to Improper Fractions
It's useful to understand the reverse process as well. To convert a mixed number back to an improper fraction, follow these steps:
-
Multiply the whole number by the denominator: Multiply 2 (the whole number) by 9 (the denominator). This results in 18.
-
Add the numerator: Add the result (18) to the numerator of the fraction (5). This gives us 23.
-
The result is the new numerator: 23 becomes the numerator of the improper fraction.
-
The denominator remains the same: The denominator stays as 9.
Therefore, 2 5/9 converts back to 23/9.
Practical Applications and Real-World Examples
Understanding the conversion between improper fractions and mixed numbers is crucial in many areas:
-
Cooking and Baking: Recipes often use fractions, and converting between improper and mixed numbers ensures accurate measurements. For instance, a recipe might call for 23/9 cups of flour, which is easier to measure if expressed as 2 5/9 cups.
-
Measurement and Construction: In construction or engineering, precise measurements are critical. Converting between fractions and mixed numbers allows for accurate calculations and avoids errors.
-
Data Analysis: When working with data that involves fractions or proportions, converting between different forms can help to interpret and present the information more clearly.
Frequently Asked Questions (FAQ)
Q: Can all improper fractions be converted to mixed numbers?
A: Yes, all improper fractions (where the numerator is greater than or equal to the denominator) can be converted to mixed numbers.
Q: What if the remainder is 0 after division?
A: If the remainder is 0, it means the improper fraction is actually a whole number. For example, 18/9 = 2. In this case, there is no fractional part in the mixed number.
Q: Are there different ways to convert an improper fraction to a mixed number?
A: While the method described above is the most common and straightforward approach, other methods exist. These methods often involve the use of long division or visual aids like number lines, but the underlying principle remains the same: dividing the numerator by the denominator to find the whole number and the remainder.
Q: Why is it important to learn this skill?
A: Mastering the conversion between improper fractions and mixed numbers is fundamental to a strong understanding of fractions. It's a building block for more advanced mathematical concepts and is essential for practical applications in various fields.
Conclusion: Mastering Fractions for a Brighter Future
Converting 23/9 to the mixed number 2 5/9 might seem like a small step, but it represents a significant milestone in understanding fractions. This skill is a cornerstone of arithmetic, underpinning many more advanced mathematical concepts. By mastering this conversion, you're not only developing your mathematical abilities but also enhancing your problem-solving skills and improving your capacity to tackle real-world challenges that involve fractions and proportions. Remember, practice is key! The more you work with fractions, the more comfortable and confident you will become. So grab a pencil and paper and try converting some more improper fractions into their mixed number equivalents. You've got this!
Latest Posts
Latest Posts
-
How Many Days Till March
Sep 18, 2025
-
16 20 As A Decimal
Sep 18, 2025
-
Is 1 3 Bigger Than 2 5
Sep 18, 2025
-
Whats 180 Days From Now
Sep 18, 2025
-
18 Cm Convert To Inches
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 23/9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.