25/9 As A Mixed Number
saludintensiva
Sep 11, 2025 · 6 min read
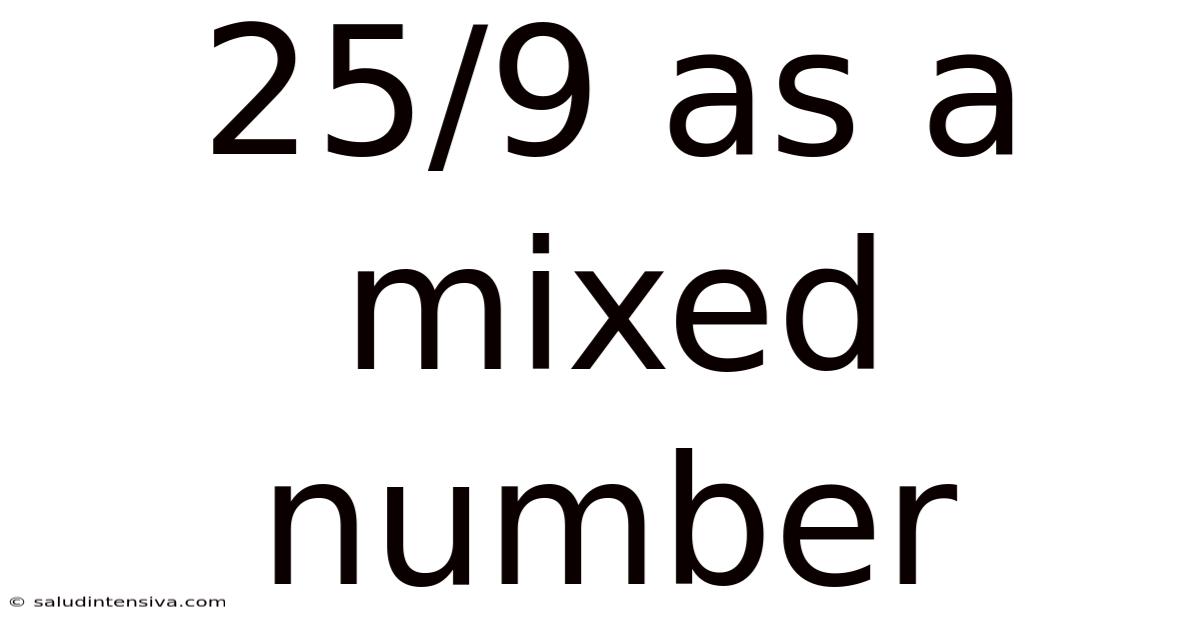
Table of Contents
Understanding 25/9 as a Mixed Number: A Comprehensive Guide
The fraction 25/9 represents a quantity greater than one whole. Understanding how to convert this improper fraction into a mixed number is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to advanced algebra. This comprehensive guide will not only show you how to convert 25/9 but also explain the underlying concepts, provide practical examples, and answer frequently asked questions. We'll delve into the process step-by-step, making this complex topic easily understandable for learners of all levels.
Introduction to Fractions and Mixed Numbers
Before we dive into converting 25/9, let's clarify the terminology. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 25/9, 7/4, 12/12). This indicates a quantity greater than or equal to one whole.
A mixed number combines a whole number and a proper fraction (e.g., 2 ¾, 5 1/3, 1 2/5). It represents a quantity greater than one whole in a more readily understandable format. Converting an improper fraction to a mixed number simplifies the representation, making it easier to visualize and work with.
Converting 25/9 to a Mixed Number: A Step-by-Step Guide
The core process involves dividing the numerator by the denominator. Here's how to do it for 25/9:
Step 1: Perform the Division
Divide the numerator (25) by the denominator (9):
25 ÷ 9 = 2 with a remainder of 7
Step 2: Identify the Whole Number
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 2.
Step 3: Identify the Remainder
The remainder from the division becomes the numerator of the fractional part of the mixed number. Here, the remainder is 7.
Step 4: Construct the Mixed Number
The denominator of the fractional part remains the same as the original denominator (9). Therefore, the mixed number is:
2 ⁷⁄₉
Therefore, 25/9 is equal to 2 ⁷⁄₉.
Visual Representation: Understanding the Concept
Imagine you have 25 equally sized pieces of pizza. Each 9 pieces make up a whole pizza. If you divide the 25 pieces into groups of 9, you'll get two full pizzas (2 x 9 = 18 pieces). You'll have 7 pieces left over (25 - 18 = 7), which represents ⁷⁄₉ of another pizza. This visually demonstrates why 25/9 equals 2 ⁷⁄₉.
Mathematical Explanation: The Algorithm Behind the Conversion
The conversion from an improper fraction to a mixed number can be expressed algebraically. Let's consider a general improper fraction a/b, where 'a' is the numerator and 'b' is the denominator (a ≥ b). The conversion follows this formula:
a/b = q + r/b
Where:
- 'a' is the numerator
- 'b' is the denominator
- 'q' is the quotient (whole number part)
- 'r' is the remainder
This formula essentially represents the division algorithm. We divide 'a' by 'b' to get the quotient 'q' and the remainder 'r'. The remainder 'r', over the original denominator 'b', forms the fractional part of the mixed number (r/b).
Practical Applications: Using Mixed Numbers in Real-Life Scenarios
Understanding the conversion between improper fractions and mixed numbers is essential for various practical applications:
-
Measurement: Imagine you're measuring a length of fabric. If you have 25/9 meters, converting it to 2 ⁷⁄₉ meters makes the measurement easier to understand and visualize.
-
Cooking: Recipes often use fractions. If a recipe calls for 25/9 cups of flour, converting it to 2 ⁷⁄₉ cups makes it easier to measure using standard measuring cups.
-
Construction: Precise measurements are crucial in construction. Converting improper fractions to mixed numbers ensures accuracy and clarity in blueprints and calculations.
-
Data Analysis: When dealing with datasets, representing data as mixed numbers can improve readability and comprehension, making analysis more efficient.
These are just a few examples; the application of converting improper fractions to mixed numbers spans across numerous fields.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. This is particularly useful when performing calculations involving mixed numbers. Here’s how to convert 2 ⁷⁄₉ back to an improper fraction:
Step 1: Multiply the whole number by the denominator
2 x 9 = 18
Step 2: Add the numerator
18 + 7 = 25
Step 3: Keep the denominator the same
The denominator remains 9.
Step 4: Construct the improper fraction
Therefore, the improper fraction is 25/9.
Frequently Asked Questions (FAQ)
Q1: Why is it important to convert improper fractions to mixed numbers?
A1: Converting improper fractions to mixed numbers makes the quantity easier to understand and visualize. It's often more intuitive to work with a mixed number (e.g., 2 ⁷⁄₉) than an improper fraction (25/9), especially in practical applications involving measurements or quantities.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, every improper fraction can be converted to a mixed number. The process always involves dividing the numerator by the denominator.
Q3: What if the remainder is zero after dividing the numerator by the denominator?
A3: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 18/9 = 2. There's no fractional part in the mixed number; it's simply the whole number quotient.
Q4: Are there any shortcuts for converting improper fractions to mixed numbers?
A4: While the step-by-step method is crucial for understanding the underlying concept, with practice, you might develop a mental shortcut for simpler fractions. However, it's always best to understand the fundamental process.
Q5: How do I convert larger improper fractions to mixed numbers?
A5: The process remains the same, regardless of the size of the numbers. You simply divide the numerator by the denominator, and the quotient and remainder will give you the whole number and fractional parts of the mixed number, respectively.
Conclusion: Mastering the Conversion of Improper Fractions to Mixed Numbers
Converting improper fractions to mixed numbers is a fundamental skill in mathematics with broad applications. This guide has provided a comprehensive explanation of the process, including step-by-step instructions, visual representations, and mathematical explanations. By understanding the underlying concepts and practicing the conversion process, you'll not only master this skill but also gain a deeper understanding of fractions and their various representations. Remember, practice makes perfect, so work through several examples to solidify your understanding and build confidence in your ability to confidently convert between improper fractions and mixed numbers.
Latest Posts
Latest Posts
-
1 2 Minus 1 3
Sep 11, 2025
-
Convert 58 Pounds To Kilograms
Sep 11, 2025
-
Can 3 4 Be Simplified
Sep 11, 2025
-
Gcf Of 85 And 51
Sep 11, 2025
-
What Is 1730 Military Time
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 25/9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.