28 50 As A Percent
saludintensiva
Sep 24, 2025 · 5 min read
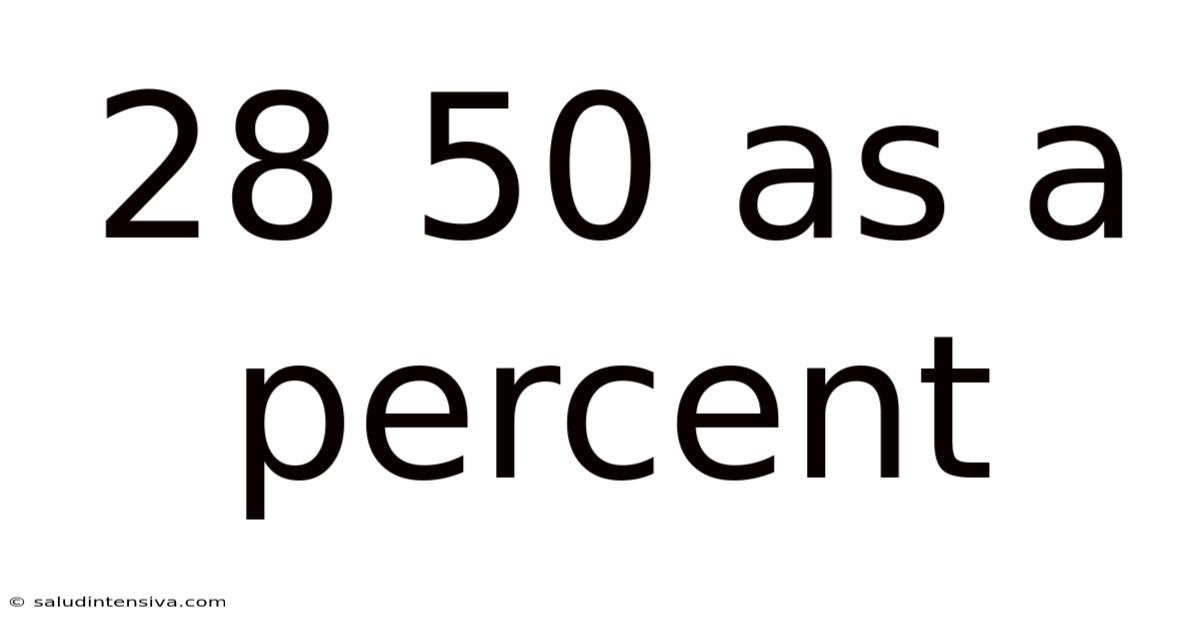
Table of Contents
Understanding 28 out of 50 as a Percentage: A Comprehensive Guide
Introduction: Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating grades and discounts to understanding statistical data and financial reports. This article provides a thorough explanation of how to determine what percentage 28 out of 50 represents, exploring various methods, and delving into the underlying concepts. We will also cover related concepts and answer frequently asked questions to ensure a comprehensive understanding. Understanding this process builds a strong foundation for more complex percentage calculations.
Method 1: Using the Basic Percentage Formula
The most straightforward method involves applying the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 28 (the number of successes or the specific portion we're interested in)
- Whole: 50 (the total number or the whole amount)
Substituting these values into the formula:
(28 / 50) x 100% = 56%
Therefore, 28 out of 50 is 56%.
Method 2: Simplifying the Fraction Before Calculation
Before applying the percentage formula, it’s often beneficial to simplify the fraction. This simplifies the arithmetic and reduces the likelihood of errors. We can simplify 28/50 by finding the greatest common divisor (GCD) of both numbers. The GCD of 28 and 50 is 2. Dividing both the numerator and denominator by 2, we get:
28 ÷ 2 = 14 50 ÷ 2 = 25
The simplified fraction is 14/25. Now, we can apply the percentage formula:
(14 / 25) x 100% = 56%
This confirms that 28 out of 50 is indeed 56%. Simplifying the fraction makes the calculation less cumbersome, especially when dealing with larger numbers.
Method 3: Using Decimal Conversion
Another approach involves converting the fraction to a decimal first and then multiplying by 100%.
First, divide the part by the whole:
28 ÷ 50 = 0.56
Then, multiply the decimal by 100%:
0.56 x 100% = 56%
This method offers an alternative pathway to the same result, highlighting the close relationship between decimals and percentages. Many calculators directly perform this division, making it a convenient method for quick calculations.
Understanding the Concept of Percentages
Percentages are a way of expressing a proportion or fraction as a number out of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Essentially, a percentage indicates how many parts of a whole you have if the whole is divided into 100 equal parts. For instance, 56% means 56 out of every 100 parts.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages has a myriad of practical applications across various fields:
- Academic Performance: Calculating grades, test scores, and overall academic performance often involves converting the number of correct answers to a percentage.
- Finance: Determining interest rates, discounts, tax rates, and profit margins all rely on percentage calculations. Understanding percentage change is crucial for tracking financial progress and making informed decisions.
- Data Analysis: Percentages are frequently used in statistical analysis to represent proportions, trends, and comparisons within datasets. Interpreting survey results, market research data, and scientific findings often requires working with percentages.
- Everyday Life: Calculating tips, sales tax, and discounts at the store, understanding nutritional information on food labels, and interpreting weather forecasts all involve using percentage concepts.
Beyond the Basics: Calculating Percentage Increase and Decrease
While the focus has been on calculating a percentage from a fraction, understanding percentage change is equally important. Let's explore how to calculate percentage increase and decrease:
- Percentage Increase: If a quantity increases from an initial value to a final value, the percentage increase is calculated as:
[(Final Value - Initial Value) / Initial Value] x 100%
- Percentage Decrease: If a quantity decreases from an initial value to a final value, the percentage decrease is calculated as:
[(Initial Value - Final Value) / Initial Value] x 100%
For example, if a product's price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
Conversely, if the price decreases from $60 to $50, the percentage decrease is:
[(60 - 50) / 60] x 100% ≈ 16.67%
Advanced Applications: Proportions and Ratios
Percentage calculations are intrinsically linked to proportions and ratios. A ratio compares two quantities, while a proportion expresses the equality of two ratios. Understanding these relationships is crucial for solving more complex problems. For example, if we know that 28 out of 50 students passed an exam, we can use this information to predict the number of students likely to pass in a larger group, using the established proportion.
Frequently Asked Questions (FAQ)
- Q: What if the "whole" number isn't a multiple of 100?
A: The method remains the same. Simply divide the "part" by the "whole," and then multiply by 100%. The resulting percentage might not be a whole number; it could be a decimal.
- Q: How can I calculate a percentage of a number?
A: To calculate x% of a number (y), you multiply the number (y) by the percentage (x/100): (x/100) * y. For example, 20% of 150 is (20/100) * 150 = 30.
- Q: Are there any shortcuts for calculating percentages?
A: Yes. For certain percentages (like 10%, 20%, 50%), simple mental arithmetic can be used. For example, 10% is simply dividing by 10, 50% is dividing by 2. Understanding these shortcuts can speed up calculations. Calculators are also invaluable tools for quick and accurate percentage computations.
- Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare different quantities, regardless of their original sizes. They allow for easier interpretation and comparison of data, making them essential in various aspects of life, from finance to academics to everyday decision-making.
Conclusion:
Calculating the percentage that 28 out of 50 represents is a straightforward yet fundamental concept with far-reaching implications. Understanding the different methods presented—using the basic formula, simplifying fractions, or decimal conversion—empowers you to approach similar problems with confidence. The ability to perform these calculations is not only crucial for academic success but also for navigating various aspects of everyday life and making informed decisions in professional and personal settings. Mastering percentage calculations builds a solid foundation for more advanced mathematical concepts and problem-solving skills. Remember, consistent practice and a clear understanding of the underlying principles are key to achieving fluency in percentage calculations.
Latest Posts
Latest Posts
-
64 Degrees C To F
Sep 24, 2025
-
What Is 1 3 Of 21
Sep 24, 2025
-
73 Acres To Square Feet
Sep 24, 2025
-
What Is Discrete In Math
Sep 24, 2025
-
How To Remove Braces Brackets
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 28 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.