2x 3y X 8 1
saludintensiva
Sep 24, 2025 · 5 min read
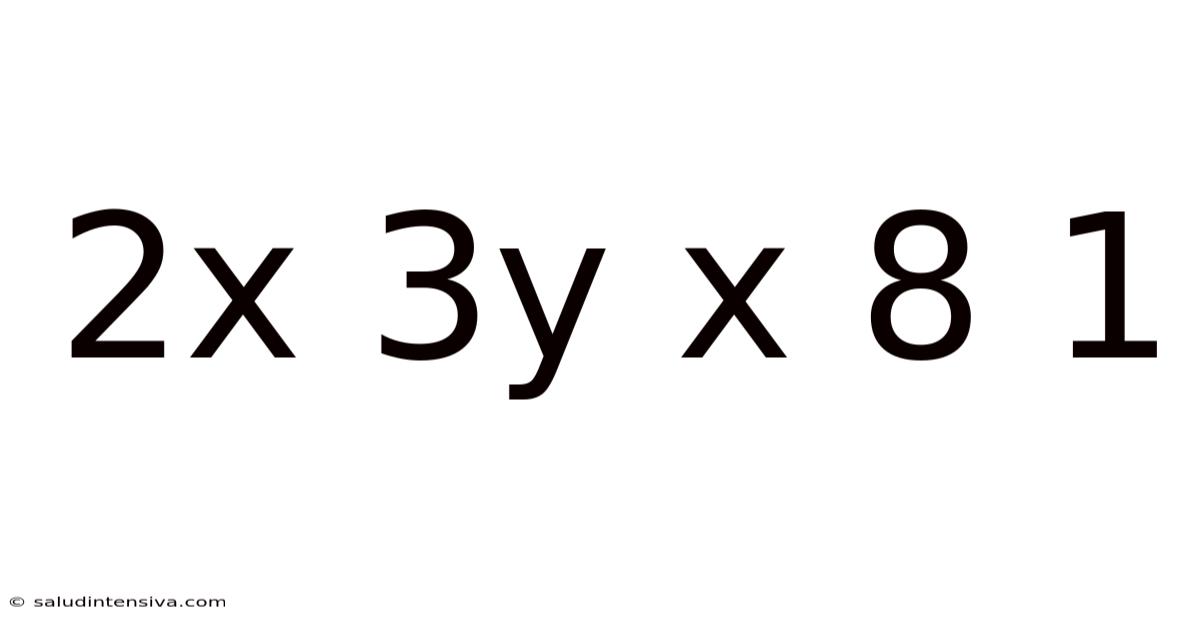
Table of Contents
Decoding the Enigma: A Deep Dive into "2x 3y x 8 1"
This seemingly simple string of characters, "2x 3y x 8 1," presents a fascinating challenge. At first glance, it might appear to be a random collection of numbers and variables. However, a closer examination reveals potential interpretations within various mathematical and logical frameworks. This article will explore different approaches to understanding this expression, examining its potential meanings and the underlying principles involved. We will delve into algebraic manipulations, consider the possibility of hidden codes, and discuss the broader implications of ambiguous notation in mathematics and problem-solving.
Introduction: Unveiling the Ambiguity
The phrase "2x 3y x 8 1" lacks explicit operators, making its interpretation highly dependent on assumed conventions and context. The absence of plus, minus, multiplication, or division signs forces us to consider multiple possible interpretations. This ambiguity, far from being a flaw, highlights the critical role of clear notation in mathematics and the power of logical reasoning in deciphering unclear instructions. We will systematically explore various possible interpretations, examining their validity and implications.
Possible Interpretations and Mathematical Explorations
1. Algebraic Interpretation:
The most straightforward interpretation treats 'x' and 'y' as variables and the numbers as coefficients. This leads to several possibilities, depending on how we interpret the juxtapositions:
-
Interpretation A: (2x)(3y)(8)(1): This assumes implicit multiplication between all terms. The simplified form would be 48xy. This is a simple, linear algebraic expression.
-
Interpretation B: 2x + 3y x 8 + 1: This interprets the juxtapositions as a mixture of multiplication and addition. Applying the order of operations (PEMDAS/BODMAS), we first perform the multiplication: 2x + 24y + 1. This is a linear equation with two variables.
-
Interpretation C: 2x + 3y × (8 + 1): This interpretation groups '8' and '1' together, resulting in: 2x + 3y × 9 = 2x + 27y.
2. Exploring Other Mathematical Operations:
Beyond the standard arithmetic operations, we could consider more advanced concepts.
-
Base Conversion: The numbers could represent digits in a different number base. However, without additional context or clues, this interpretation remains speculative. For example, if we were to assume base 10, there's no clear connection between the given numbers and a meaningful result.
-
Matrix Representation: If 'x' and 'y' represent matrices, then the expression could lead to matrix multiplication. However, the dimensions of the matrices would need to be specified to perform this operation. The absence of this information renders this interpretation currently inconclusive.
3. The Significance of Missing Operators:
The absence of explicit mathematical operators underscores a critical aspect of mathematical communication: the importance of precision. Ambiguous notation can lead to misinterpretations and incorrect results. Clear and consistent use of operators ensures that the intended mathematical operations are accurately conveyed. This is crucial not just in academic settings but also in real-world applications, where errors can have significant consequences.
Expanding the Scope: Logic, Codes, and Problem-Solving
Beyond the purely mathematical realm, we can explore alternative perspectives:
-
Hidden Codes: The string could represent a coded message. This requires a deeper understanding of potential coding schemes. We would need further information or context to decipher it, such as a key or algorithm. Is it a substitution cipher? A transposition cipher? Without additional context, we can't effectively decode this as a hidden message.
-
Logical Puzzles: The expression could form part of a larger logical puzzle. Additional information or constraints would be necessary to solve such a puzzle. For instance, we might be given additional equations or relationships between x and y.
-
Symbolic Representation: "2x 3y x 8 1" might represent a symbolic system rather than a numerical expression. The symbols could represent objects or concepts within a specific system, and the juxtaposition might define a relationship or operation within that system. Without understanding this symbolic system, we cannot interpret the meaning.
-
Pattern Recognition: The sequence itself may contain a hidden pattern or sequence that isn't immediately apparent. Exploring different perspectives and patterns could reveal hidden structures, but without a wider context, this remains highly speculative.
The Importance of Context and Further Information
The lack of context significantly hinders our ability to interpret "2x 3y x 8 1" definitively. To arrive at a meaningful solution, we would need further information, including:
-
The source of the expression: Where did this string of characters originate? Knowing the source could provide valuable clues about its intended meaning. A textbook problem would likely have a different interpretation than a coded message.
-
The intended audience: Who is this expression aimed at? The intended audience could influence the level of complexity and the expected method of interpretation.
-
Additional constraints or equations: Are there any additional equations or relationships involving 'x' and 'y'? These constraints could significantly narrow down the possibilities and lead to a unique solution.
-
The underlying mathematical system: Is this expression part of a specific mathematical system or framework, such as linear algebra, group theory, or a novel mathematical construct? Understanding the system would inform our choice of interpretation.
Frequently Asked Questions (FAQ)
-
Q: Is there a single correct answer? A: No, without additional context, there isn't a single correct answer. Multiple interpretations are possible, each with its own validity.
-
Q: What are the limitations of this analysis? A: The main limitation is the lack of context. With additional information, a more precise and definitive interpretation would be possible.
-
Q: Can this expression be simplified further? A: The simplification depends on the interpretation. Under the algebraic interpretation (Interpretation A), it simplifies to 48xy. Other interpretations lead to different simplified forms.
Conclusion: The Value of Ambiguity in Learning
While the ambiguity of "2x 3y x 8 1" presents a challenge, it also underscores the importance of clear communication and precise notation in mathematics and problem-solving. The exploration of different interpretations highlights the diverse ways in which seemingly simple expressions can be understood. This exercise in ambiguity underscores the need for clear communication and critical thinking skills. It emphasizes the importance of questioning assumptions, considering multiple perspectives, and seeking additional information when faced with unclear instructions or ambiguous notations. The process of exploring different possibilities enhances problem-solving skills and develops a deeper understanding of mathematical principles and their application. The inherent ambiguity encourages a more nuanced and flexible approach to problem-solving, thereby enriching the learning process. Future investigations into similar expressions would ideally incorporate the crucial element of context to unlock definitive and meaningful solutions.
Latest Posts
Latest Posts
-
Inch Conversion Decimal To Fraction
Sep 24, 2025
-
Formula For Uniformly Accelerated Motion
Sep 24, 2025
-
64 Degrees C To F
Sep 24, 2025
-
What Is 1 3 Of 21
Sep 24, 2025
-
73 Acres To Square Feet
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2x 3y X 8 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.