3 1/4 - 1 3/4
saludintensiva
Sep 15, 2025 · 6 min read
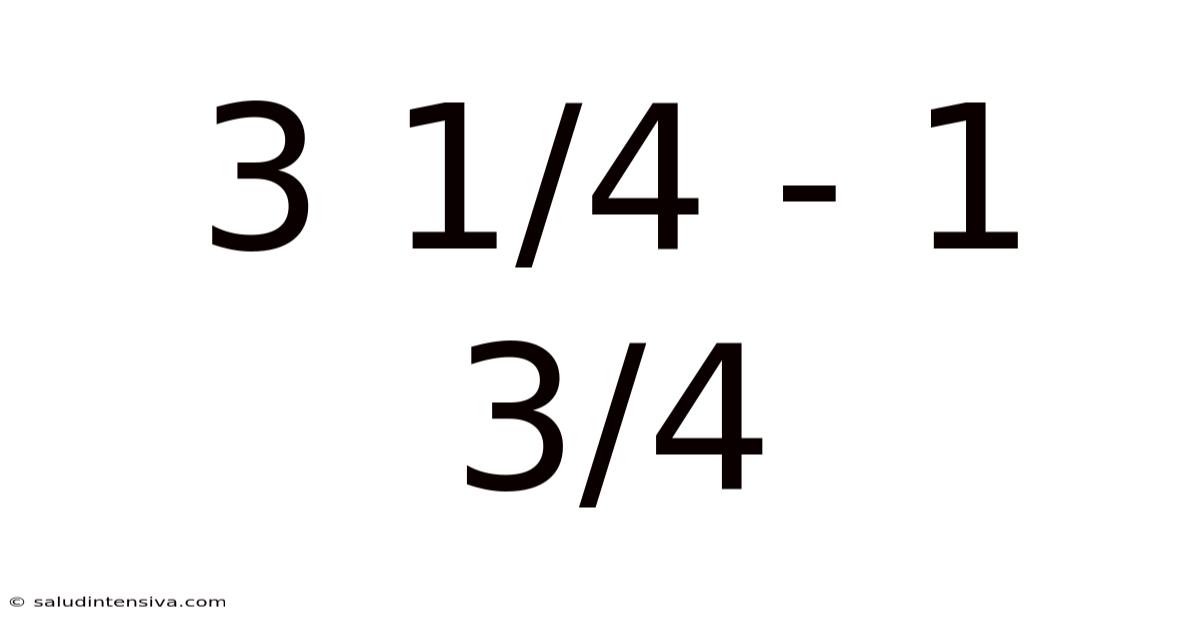
Table of Contents
Deconstructing 3 1/4 - 1 3/4: A Deep Dive into Subtraction of Mixed Numbers
This article provides a comprehensive guide to solving the subtraction problem 3 1/4 - 1 3/4, explaining the process step-by-step and delving into the underlying mathematical principles. We'll cover various methods, address common challenges, and explore related concepts to solidify your understanding of mixed number subtraction. Understanding this seemingly simple problem unlocks a broader understanding of fractions and their applications in everyday life. This guide is designed for students, educators, and anyone looking to refresh their arithmetic skills.
Understanding Mixed Numbers
Before tackling the subtraction, let's refresh our understanding of mixed numbers. A mixed number combines a whole number and a fraction. For example, 3 1/4 represents three whole units and one-quarter of another unit. Understanding the components – the whole number and the fractional part – is crucial for performing calculations.
Method 1: Converting to Improper Fractions
This is a common and effective method for subtracting mixed numbers. The first step involves converting both mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Step 1: Convert 3 1/4 to an improper fraction.
To do this, we multiply the whole number (3) by the denominator (4) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
3 1/4 = (3 * 4 + 1) / 4 = 13/4
Step 2: Convert 1 3/4 to an improper fraction.
Following the same process:
1 3/4 = (1 * 4 + 3) / 4 = 7/4
Step 3: Perform the Subtraction.
Now that we have improper fractions, we can subtract them:
13/4 - 7/4 = (13 - 7) / 4 = 6/4
Step 4: Simplify the Result.
The result 6/4 is an improper fraction. We simplify it by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2:
6/4 = (6 ÷ 2) / (4 ÷ 2) = 3/2
Step 5: Convert back to a Mixed Number (Optional).
While 3/2 is a perfectly acceptable answer, we can convert it back to a mixed number if desired. We divide the numerator (3) by the denominator (2):
3 ÷ 2 = 1 with a remainder of 1.
Therefore, 3/2 = 1 1/2
Thus, 3 1/4 - 1 3/4 = 1 1/2
Method 2: Subtracting Whole Numbers and Fractions Separately
This method involves subtracting the whole numbers and the fractions separately. However, it requires careful attention when the fraction in the subtrahend (the number being subtracted) is larger than the fraction in the minuend (the number from which we are subtracting).
Step 1: Attempt Direct Subtraction (If Possible).
Let's try subtracting the whole numbers and fractions directly:
3 - 1 = 2 1/4 - 3/4 = -2/4
Since we cannot have a negative fraction, this method fails in this specific case. This highlights the limitation of this method when the fraction being subtracted is larger.
Method 3: Borrowing from the Whole Number
This is the most robust method for subtracting mixed numbers, especially when the fraction in the subtrahend is larger than the fraction in the minuend. It involves "borrowing" from the whole number to increase the fraction.
Step 1: Borrow from the Whole Number.
We need to borrow one whole unit (4/4) from the whole number 3. This transforms 3 1/4 into:
3 1/4 = 2 + 4/4 + 1/4 = 2 5/4
Step 2: Perform the Subtraction.
Now we can subtract:
2 5/4 - 1 3/4 = (2 - 1) + (5/4 - 3/4) = 1 + 2/4
Step 3: Simplify the Result.
Simplify the fraction 2/4 by dividing both numerator and denominator by their GCD (2):
1 + 2/4 = 1 + 1/2 = 1 1/2
This method arrives at the same correct answer as Method 1.
Visualizing the Subtraction
It can be helpful to visualize the subtraction using diagrams or models. Imagine three and a quarter pizzas. If you take away one and three-quarters pizzas, you will be left with one and a half pizzas. This visual representation reinforces the concept.
Mathematical Properties and Concepts
Subtracting mixed numbers directly relates to fundamental concepts in arithmetic, including:
- Fractions: Understanding the concept of fractions, their representation, and operations is fundamental to solving the problem.
- Improper Fractions: Converting mixed numbers to improper fractions streamlines the subtraction process.
- Greatest Common Divisor (GCD): Simplifying fractions requires finding the GCD of the numerator and denominator.
- Equivalence of Fractions: Borrowing involves expressing a whole number as an equivalent fraction with the same denominator as the existing fraction.
- Number Line: Visualizing the problem on a number line can aid in understanding the magnitude of the subtraction.
Common Mistakes and How to Avoid Them
- Incorrect Conversion to Improper Fractions: Double-check your calculations when converting mixed numbers to improper fractions.
- Forgetting to Simplify: Always simplify the final answer to its lowest terms.
- Ignoring Negative Fractions: Be aware of the necessity for borrowing when the fraction in the subtrahend is larger than the fraction in the minuend.
- Arithmetic Errors: Careful calculation is essential to avoid simple arithmetic errors throughout the process.
Frequently Asked Questions (FAQ)
Q: Can I subtract mixed numbers directly without converting to improper fractions? A: While sometimes possible, it's often more efficient and less prone to error to convert to improper fractions first, particularly when the fraction in the subtrahend is larger.
Q: What if the denominators are different? A: If the denominators are different, you must find a common denominator before subtracting the fractions. This involves finding the least common multiple (LCM) of the denominators.
Q: Are there other methods to solve this problem? A: While the methods described are the most common and efficient, there are other approaches involving decimal conversions or using visual aids. However, mastering the methods described provides a strong foundation for more complex fraction problems.
Q: Why is it important to understand this concept? A: Understanding mixed number subtraction is crucial for various applications, including cooking, construction, sewing, and many other everyday tasks involving measurements and quantities.
Conclusion
Solving 3 1/4 - 1 3/4 effectively demonstrates the importance of understanding and applying various techniques in fraction arithmetic. By mastering these methods, not only can you confidently solve this specific problem, but you also develop a strong foundation for tackling more complex fraction problems and strengthen your overall mathematical skills. Remember to practice regularly and choose the method that feels most comfortable and efficient for you. Consistent practice will solidify your understanding and build confidence in handling similar problems in the future. The key is to break down the problem into manageable steps and to understand the underlying mathematical principles. By understanding the why behind each step, you'll develop a more intuitive and robust understanding of fraction arithmetic.
Latest Posts
Latest Posts
-
3 5 X 1 2
Sep 15, 2025
-
How To Solve Fraction Problems
Sep 15, 2025
-
Change Decimal To Mixed Number
Sep 15, 2025
-
Multiples Of 2 And 5
Sep 15, 2025
-
3 14 As A Decimal
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 1/4 - 1 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.