3 5 X 1 2
saludintensiva
Sep 15, 2025 · 5 min read
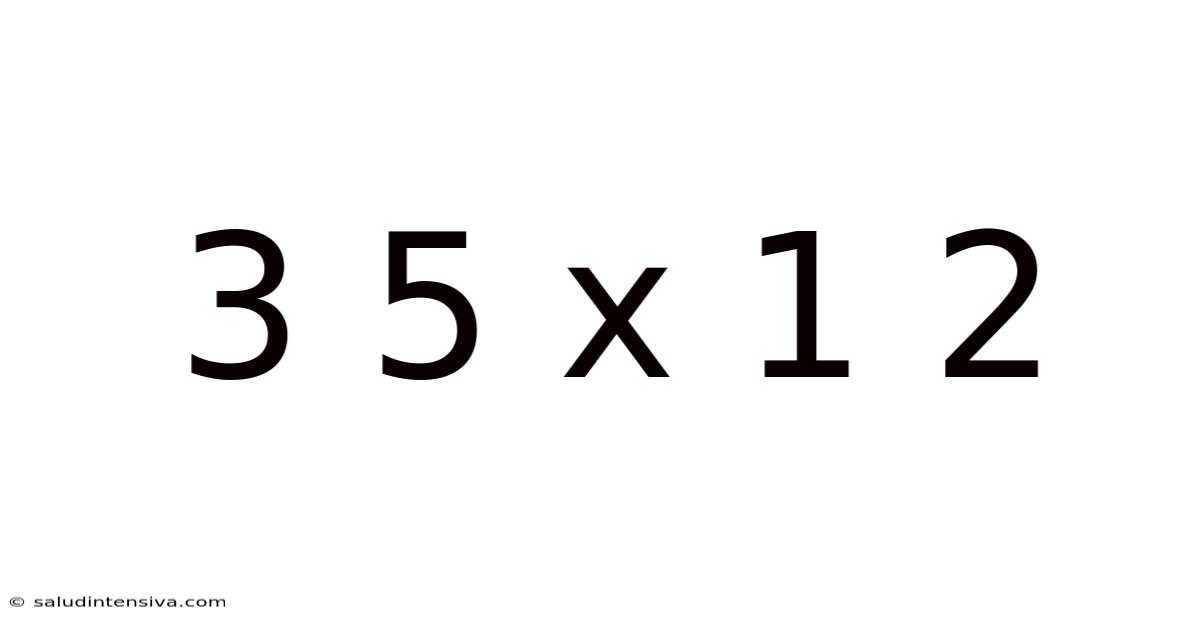
Table of Contents
Decoding 3.5 x 1.2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 3.5 multiplied by 1.2, unraveling the underlying mathematical principles and demonstrating its relevance across various fields. We will move beyond the basic arithmetic to understand the concept of decimal multiplication, its practical applications, and explore different methods for solving this problem and similar ones. Understanding this fundamental calculation is key to mastering more complex mathematical concepts and real-world problem-solving.
Understanding Decimal Multiplication
Before diving into the calculation of 3.5 x 1.2, let's solidify our understanding of decimal multiplication. Decimals represent fractions where the denominator is a power of 10 (10, 100, 1000, and so on). For example, 3.5 is equivalent to 3 and 5/10 or 35/10, and 1.2 is equivalent to 1 and 2/10 or 12/10.
Therefore, multiplying 3.5 x 1.2 is essentially the same as calculating (35/10) x (12/10). This can be simplified to (35 x 12) / (10 x 10) = 420/100. Converting this fraction back to a decimal gives us 4.2.
Method 1: Standard Multiplication Algorithm
The standard multiplication algorithm, learned in elementary school, provides a structured approach to solving this problem. Let's break it down step-by-step:
-
Ignore the decimal points: Initially, treat 3.5 and 1.2 as whole numbers: 35 and 12.
-
Multiply as usual: Perform standard multiplication:
35 x 12 ---- 70 (35 x 2) 350 (35 x 10) ---- 420 -
Place the decimal point: Now, count the total number of decimal places in the original numbers (3.5 and 1.2). There's one decimal place in 3.5 and one in 1.2, making a total of two decimal places. In the result (420), move the decimal point two places to the left, resulting in 4.2.
Therefore, 3.5 x 1.2 = 4.2
Method 2: Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can use this property to break down the multiplication into simpler steps:
-
Break down 1.2: Express 1.2 as 1 + 0.2.
-
Apply the distributive property: 3.5 x 1.2 = 3.5 x (1 + 0.2) = (3.5 x 1) + (3.5 x 0.2)
-
Calculate the individual multiplications:
- 3.5 x 1 = 3.5
- 3.5 x 0.2 = 0.7 (This can be calculated as (35/10) x (2/10) = 70/100 = 0.7)
-
Add the results: 3.5 + 0.7 = 4.2
Therefore, using the distributive property, we again arrive at the answer: 3.5 x 1.2 = 4.2
Method 3: Fraction Multiplication
As mentioned earlier, we can convert the decimals to fractions and then perform the multiplication:
-
Convert decimals to fractions: 3.5 = 35/10 and 1.2 = 12/10
-
Multiply the fractions: (35/10) x (12/10) = (35 x 12) / (10 x 10) = 420/100
-
Simplify the fraction: 420/100 simplifies to 42/10
-
Convert the fraction back to a decimal: 42/10 = 4.2
This method reinforces the fundamental concept of decimal multiplication as fraction multiplication.
Real-World Applications of Decimal Multiplication
The seemingly simple calculation of 3.5 x 1.2 has numerous practical applications across diverse fields:
- Everyday Finances: Calculating the total cost of 3.5 kg of apples at $1.2 per kg.
- Construction and Engineering: Determining the area of a rectangular space measuring 3.5 meters by 1.2 meters.
- Science and Measurement: Calculating the volume or density of a substance. For example, if a liquid has a density of 1.2 g/mL and you have 3.5 mL of it, the total mass is 3.5 x 1.2 = 4.2 g.
- Cooking and Baking: Scaling recipes. If a recipe calls for 1.2 cups of flour and you want to make 3.5 times the recipe, you would need 3.5 x 1.2 = 4.2 cups of flour.
- Data Analysis: In statistical analysis, calculations involving decimals are commonplace. For instance, calculating the mean of a dataset with decimal values often involves multiplication.
Expanding the Concept: Multiplying Larger Decimals
The methods discussed above can be applied to multiplying larger decimals as well. The key is to remember the steps:
- Ignore the decimal points initially.
- Multiply as you would with whole numbers.
- Count the total number of decimal places in the original numbers.
- Place the decimal point in the result by moving it to the left the number of places counted in step 3.
For example, let's consider 12.5 x 3.78:
-
Ignore decimal points: 125 x 378 = 47250
-
Count decimal places: 12.5 has one decimal place, and 3.78 has two decimal places, totaling three decimal places.
-
Place decimal point: Move the decimal point three places to the left in 47250, resulting in 47.250 or 47.25.
Therefore, 12.5 x 3.78 = 47.25
Frequently Asked Questions (FAQ)
Q: What if I have more than two decimal numbers to multiply?
A: The process remains the same. Multiply the numbers as whole numbers first, then count the total number of decimal places in all the numbers involved and adjust the decimal place in your final answer accordingly.
Q: What happens if the result of the multiplication has fewer digits than the total number of decimal places?
A: You'll need to add leading zeros to the left of the result to accommodate the required number of decimal places. For instance, if you have 0.02 x 0.05 = 0.001, you need the leading zeros to ensure the correct number of decimal places.
Q: Can I use a calculator to solve decimal multiplication problems?
A: Yes, calculators are a convenient tool for performing decimal multiplication, especially for more complex problems. However, understanding the underlying principles is crucial for developing a strong mathematical foundation.
Conclusion: Mastering the Fundamentals
The seemingly simple calculation of 3.5 x 1.2 provides a gateway to understanding the broader concept of decimal multiplication. By mastering this fundamental operation and exploring different solution methods, you enhance your mathematical skills and build a strong foundation for tackling more complex calculations in various academic and professional fields. Remember the three key steps: ignore the decimals initially, multiply the whole numbers, and then carefully place the decimal point in the final answer based on the total number of decimal places in the original numbers. This understanding is not just about getting the right answer but about developing a deep comprehension of the underlying mathematical principles. From everyday budgeting to complex scientific calculations, the ability to confidently handle decimal multiplication is an invaluable asset.
Latest Posts
Latest Posts
-
18 Cm Converted To Inches
Sep 15, 2025
-
What Is 9 12 Equal To
Sep 15, 2025
-
4 3 To The 2nd Power
Sep 15, 2025
-
Whats Equal To 1 4
Sep 15, 2025
-
1 3 Plus 1 6
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 5 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.