3 10 X 2 3
saludintensiva
Sep 13, 2025 · 5 min read
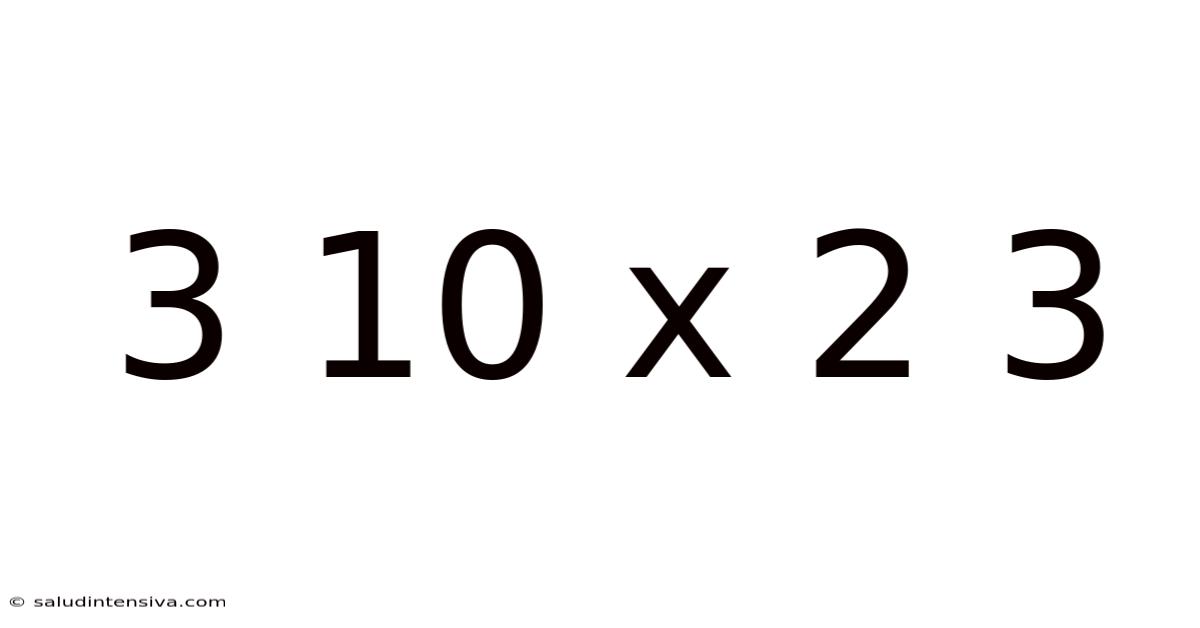
Table of Contents
Decoding the Enigma: A Deep Dive into 3, 10, x, 2, 3
This article explores the multifaceted interpretations and potential meanings behind the seemingly simple sequence "3, 10, x, 2, 3." We'll delve into various mathematical, logical, and even creative perspectives to unravel the mystery of this enigmatic sequence, aiming to provide a comprehensive and insightful analysis for readers of all backgrounds. The seemingly random arrangement offers an opportunity to explore pattern recognition, problem-solving skills, and the boundless nature of mathematical and logical thinking.
Introduction: The Allure of the Unknown
The sequence "3, 10, x, 2, 3" presents a captivating challenge. The presence of the unknown variable 'x' immediately sparks curiosity and invites exploration. Is this a simple arithmetic progression? A complex geometric sequence? Or something entirely different? The beauty of this puzzle lies in its ambiguity, allowing for multiple valid approaches and interpretations. We will examine various methods to potentially solve for 'x,' uncovering the underlying logic or pattern that may govern the sequence. This exercise will sharpen our analytical thinking and demonstrate the power of diverse problem-solving techniques.
Mathematical Approaches: Unveiling Potential Patterns
Several mathematical approaches can be employed to understand the relationship between the known numbers and potentially determine the value of 'x.'
1. Arithmetic Progressions and Differences:
Let's begin by examining the differences between consecutive known numbers.
- The difference between 10 and 3 is 7.
- The difference between 2 and 10 is -8.
This immediately reveals that a simple arithmetic progression is unlikely. The inconsistency in differences suggests a more complex relationship.
2. Geometric Progressions and Ratios:
Next, let's consider geometric progressions, where consecutive numbers have a constant ratio.
- The ratio between 10 and 3 is approximately 3.33.
- The ratio between 2 and 10 is 0.2.
Again, the lack of consistency points against a simple geometric progression.
3. Polynomial Functions:
A more sophisticated approach involves fitting a polynomial function to the known data points. This involves finding a polynomial equation that accurately predicts the value of 'x' based on its position in the sequence. This approach is more suitable for larger sequences with more data points, but it can still offer insight. However, given only four data points, accurately fitting a polynomial might not provide a unique or reliable solution for 'x'. The possibility of multiple valid polynomial functions fitting this data set is high.
4. Modular Arithmetic:
Exploring modular arithmetic might reveal hidden patterns. Let's examine the remainders when the numbers are divided by a certain modulus. For instance, using modulo 7:
- 3 mod 7 = 3
- 10 mod 7 = 3
- 2 mod 7 = 2
This approach doesn't immediately reveal a clear pattern, but further exploration with different moduli might unveil a hidden relationship.
Logical and Creative Approaches: Beyond the Numbers
While mathematical approaches are crucial, exploring non-mathematical perspectives can unlock additional interpretations.
1. Pattern Recognition and Sequencing:
Stepping back from purely numerical analysis, let's examine the sequence from a broader pattern recognition perspective. Are there any patterns in the digits themselves? Any recurring sequences or relationships? For example, notice that the sequence ends with '3', mirroring the start. This might suggest a cyclic or repeating pattern. However, without further data, it remains speculative.
2. Contextual Interpretation:
The sequence could represent coded information or a symbolic representation within a specific context. Without knowing the origin or purpose of the sequence, it's impossible to make definitive interpretations based on context.
3. Creative Interpretations:
The sequence could be a starting point for a creative writing prompt, a musical composition, or a visual art piece. The open-ended nature of the puzzle encourages creative thinking and exploration.
Advanced Mathematical Concepts: Exploring Possibilities
To further explore the possibilities, let’s consider more advanced mathematical concepts.
1. Recurrence Relations:
A recurrence relation defines a sequence recursively, where each term depends on the preceding terms. It's possible to create a recurrence relation that fits the given sequence, although it might not be unique.
2. Number Theory:
Exploring number-theoretic properties of the numbers might reveal patterns or relationships. This could involve examining factors, prime factorization, or other number-theoretic concepts. However, without more data, it's difficult to draw firm conclusions.
3. Combinatorics:
Combinatorial analysis could be applied if the sequence represents combinations or permutations of a set of objects. This approach would require additional information or context about the sequence's origin.
Addressing Potential Obstacles and Limitations
The main obstacle in definitively solving for 'x' is the limited amount of data. With only four data points and one unknown, there are multiple potential solutions and interpretations. The ambiguity highlights the importance of having sufficient data when attempting to identify patterns or solve mathematical puzzles. More data points would allow for a more precise and confident analysis.
Frequently Asked Questions (FAQ)
Q1: Is there a single definitive solution for 'x'?
A1: No, given the limited information, there isn't a single, definitive mathematical solution for 'x.' Multiple mathematical functions could potentially fit the given data points.
Q2: What are the limitations of the mathematical approaches?
A2: The limitations stem from the small sample size. With more data points, more robust statistical and mathematical analyses could be employed to determine a more reliable solution for 'x' and the underlying pattern.
Q3: Can the sequence have a non-mathematical interpretation?
A3: Absolutely! The sequence could be a code, a symbol, or a starting point for creative expression. Its interpretation depends heavily on the context in which it appears.
Conclusion: The Enduring Mystery and the Value of Exploration
The sequence "3, 10, x, 2, 3" serves as a potent reminder of the complexity and beauty inherent in mathematical and logical problem-solving. While a definitive solution for 'x' remains elusive given the limited data, the journey of exploring various approaches has provided valuable insights into pattern recognition, mathematical techniques, and the power of creative thinking. The ambiguity of the sequence encourages further investigation and exploration, showcasing the boundless possibilities of mathematical and logical reasoning. The exercise highlights the importance of having sufficient data for accurate analysis and the value of considering various perspectives when tackling complex problems. Ultimately, the "mystery" of 'x' underscores the ongoing learning and discovery that accompanies mathematical pursuits. The process of seeking a solution, even without a definitive answer, has proven to be enriching and rewarding in its own right.
Latest Posts
Latest Posts
-
How Long Is 193 Minutes
Sep 13, 2025
-
Lcm Of 24 And 21
Sep 13, 2025
-
2 To The 3 Power
Sep 13, 2025
-
What Time Is 21 40
Sep 13, 2025
-
27 Out Of 30 Percentage
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 10 X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.