3 100 As A Percent
saludintensiva
Sep 14, 2025 · 5 min read
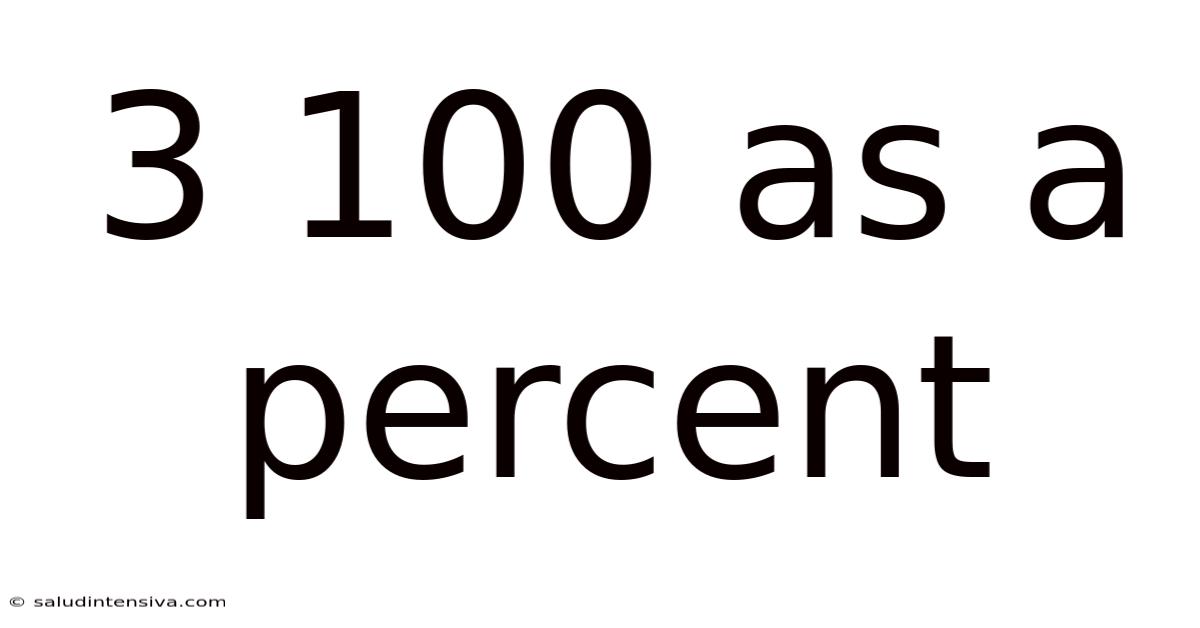
Table of Contents
3/100 as a Percent: Understanding Fractions, Decimals, and Percentages
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday calculations. This comprehensive guide will walk you through understanding how to express 3/100 as a percentage, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll explore the relationship between fractions, decimals, and percentages, and address frequently asked questions to ensure you grasp this essential mathematical concept fully.
Understanding Fractions, Decimals, and Percentages
Before diving into the specifics of 3/100, let's review the core concepts:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 3/100, 3 is the numerator and 100 is the denominator. This means we have 3 parts out of a total of 100 equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the decimal point separating the whole number from the fractional part. For instance, 0.03 is a decimal representation.
-
Percentages: Percentages represent parts of a whole as a fraction of 100. The symbol "%" signifies "per hundred." So, 3% means 3 out of 100.
Converting 3/100 to a Percentage
Converting a fraction to a percentage involves two simple steps:
-
Convert the fraction to a decimal: To do this, divide the numerator (3) by the denominator (100):
3 ÷ 100 = 0.03
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol:
0.03 x 100 = 3%
Therefore, 3/100 is equal to 3%.
Visualizing 3/100 as a Percentage
Imagine a 100-square grid. If you shade 3 squares, you've shaded 3 out of 100 squares, representing 3/100 or 3%. This visual representation helps solidify the understanding of the concept. You can apply this visualization to various scenarios, like calculating percentages of discounts, grades, or survey results.
Practical Applications of 3/100 (3%)
Understanding 3% as a representation of 3/100 has many practical applications:
-
Finance: A 3% interest rate on a loan means you pay 3 units of currency for every 100 units borrowed. Similarly, a 3% discount on an item means you save 3 units of currency for every 100 units of the original price.
-
Statistics: In data analysis, 3% might represent the percentage of a population with a specific characteristic. For instance, if 3 out of 100 people surveyed prefer a particular product, that translates to a 3% preference rate.
-
Everyday Life: Calculating tips, sales tax, or even understanding proportions in recipes often involves working with percentages. Knowing how to convert fractions like 3/100 to percentages is crucial for performing these everyday calculations accurately.
Working with Larger Fractions and Percentages
The method for converting fractions to percentages remains consistent, regardless of the size of the fraction. Let's consider a larger fraction, such as 15/200:
-
Convert to a decimal: 15 ÷ 200 = 0.075
-
Convert to a percentage: 0.075 x 100 = 7.5%
So, 15/200 equals 7.5%. This illustrates that the principle remains the same; you simply divide the numerator by the denominator and then multiply by 100.
Understanding Percentage Increase and Decrease
Percentages are also used to represent increases or decreases in quantities. For example, if a price increases by 3%, it means the new price is 103% of the original price (100% + 3%). Conversely, a 3% decrease means the new value is 97% of the original value (100% - 3%).
Solving Percentage Problems: A Step-by-Step Approach
Let's examine a practical problem to further illustrate the application of percentage calculations:
Problem: A store offers a 3% discount on all items. If an item costs $150, how much is the discount and what is the final price?
Solution:
-
Calculate the discount: Multiply the original price by the discount percentage (as a decimal): $150 x 0.03 = $4.50
-
Calculate the final price: Subtract the discount from the original price: $150 - $4.50 = $145.50
Therefore, the discount is $4.50, and the final price is $145.50.
Advanced Percentage Calculations: Proportion and Ratio
Percentage calculations are closely related to the concepts of proportion and ratio. A ratio compares two quantities, while a proportion states that two ratios are equal. Understanding these concepts enhances your ability to solve more complex percentage problems. For instance, if we know that 3 out of 100 items are defective, we can use proportions to determine how many defective items are expected in a larger batch of, say, 500 items.
Frequently Asked Questions (FAQ)
Q1: How do I convert a percentage back to a fraction?
A1: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 3% becomes 3/100, which is already in its simplest form.
Q2: Can I have a percentage greater than 100%?
A2: Yes, you can. A percentage greater than 100% indicates a value exceeding the original value. For example, a 110% increase means the new value is 110% of the original value.
Q3: How do I calculate the percentage change between two numbers?
A3: Calculate the difference between the two numbers, divide this difference by the original number, and then multiply by 100 to express the result as a percentage. For example, if a value increases from 100 to 103, the percentage increase is ((103-100)/100) * 100 = 3%.
Q4: What if the denominator of the fraction is not 100?
A4: If the denominator is not 100, you still follow the same process: divide the numerator by the denominator to get a decimal and then multiply by 100 to get the percentage.
Conclusion
Understanding how to represent 3/100 as a percentage, namely 3%, is a crucial skill in various aspects of life. This process involves converting the fraction to a decimal and then multiplying by 100. By mastering this concept, you'll be better equipped to handle various percentage-related calculations, from simple everyday tasks to more complex mathematical problems. Remember that percentages are simply a way to express fractions as parts of a hundred, making them a useful tool for understanding and comparing proportions. Practice is key to solidifying your understanding and developing proficiency in working with percentages.
Latest Posts
Latest Posts
-
119 Degrees Fahrenheit To Celsius
Sep 15, 2025
-
1 8 Times 1 4
Sep 15, 2025
-
Gcf Of 16 And 9
Sep 15, 2025
-
3 1 2 In Improper Fraction
Sep 15, 2025
-
13 3 As A Decimal
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 100 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.