3 4 1 6 Simplify
saludintensiva
Sep 17, 2025 · 6 min read
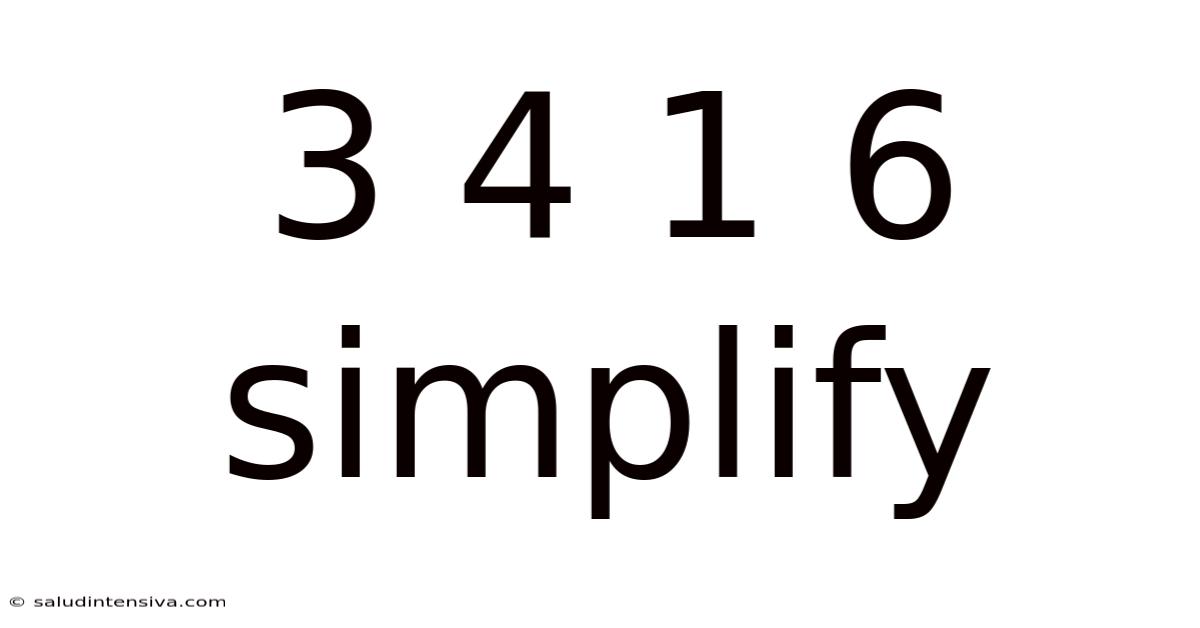
Table of Contents
Decoding the Mystery: A Deep Dive into Simplifying the Ratio 3:4:1:6
Understanding ratios is a fundamental skill in various fields, from cooking and construction to finance and chemistry. This article will explore the simplification of the ratio 3:4:1:6, providing a clear, step-by-step approach suitable for learners of all levels. We'll delve into the underlying mathematical principles, explore practical applications, and answer frequently asked questions to ensure a comprehensive understanding of this concept. By the end, you'll not only know how to simplify this specific ratio but also possess the tools to tackle similar problems with confidence.
Introduction to Ratios and Simplification
A ratio is a mathematical comparison of two or more quantities. It shows the relative sizes of the quantities. The ratio 3:4:1:6 indicates that we have four quantities in the proportions 3, 4, 1, and 6. Simplifying a ratio means finding an equivalent ratio with smaller, whole numbers while maintaining the same proportions. This is achieved by finding the greatest common divisor (GCD) of all the numbers in the ratio and dividing each number by the GCD. This process ensures that the relationship between the quantities remains unchanged, only represented in a more concise form.
Step-by-Step Simplification of 3:4:1:6
Let's break down the simplification of the ratio 3:4:1:6 into manageable steps:
1. Find the Greatest Common Divisor (GCD):
The first step is crucial – finding the GCD of the numbers 3, 4, 1, and 6. The GCD is the largest number that divides evenly into all the numbers. Several methods exist for finding the GCD, including:
-
Listing Factors: List all the factors of each number and identify the largest factor common to all. Factors of 3 are 1 and 3. Factors of 4 are 1, 2, and 4. Factors of 1 is only 1. Factors of 6 are 1, 2, 3, and 6. The only common factor is 1.
-
Prime Factorization: Express each number as a product of its prime factors. Then, identify the common prime factors and multiply them together. The prime factorization method is particularly helpful with larger numbers.
- 3 = 3
- 4 = 2 x 2
- 1 = 1
- 6 = 2 x 3
In this case, there are no common prime factors among 3, 4, 1, and 6 other than 1.
2. Dividing by the GCD:
Since the GCD of 3, 4, 1, and 6 is 1, dividing each number by 1 doesn't change their values. Therefore, the ratio 3:4:1:6 is already in its simplest form.
Conclusion: The ratio 3:4:1:6 is already in its simplest form. It cannot be further reduced while maintaining the proportional relationships between the four quantities.
Practical Applications of Ratios
Understanding and simplifying ratios is essential in numerous real-world scenarios:
-
Recipe Scaling: Recipes often use ratios to specify ingredient proportions. If you need to double or halve a recipe, you need to understand and adjust the ratios accordingly.
-
Construction and Engineering: Ratios are crucial in construction and engineering for maintaining accurate proportions in designs and blueprints. Scaling models or plans often involves working with ratios.
-
Finance and Investing: Ratios are widely used in financial analysis to assess the performance of companies and investments. Examples include price-to-earnings ratios (P/E ratios) and debt-to-equity ratios.
-
Science and Chemistry: In chemistry, ratios are essential for determining the proportions of elements in chemical compounds and balancing chemical equations.
-
Mapping and Scale Drawings: Maps and scale drawings utilize ratios to represent real-world distances and sizes in a smaller, manageable format.
Understanding Proportions within the Ratio 3:4:1:6
While the ratio 3:4:1:6 cannot be numerically simplified, it's crucial to understand the proportional relationships it represents. The numbers 3, 4, 1, and 6 define the relative sizes of four different quantities. For example, if the first quantity is 3 units, the second will be 4 units, the third 1 unit, and the fourth 6 units. Any multiple of these numbers will maintain the same proportional relationship. For instance, 6:8:2:12 is an equivalent, albeit unsimplified, ratio.
Advanced Ratio Concepts
Let's explore some more complex scenarios related to ratios. This will equip you with a more thorough understanding of ratio manipulation.
Dealing with Ratios Containing Fractions or Decimals:
Sometimes, you might encounter ratios with fractions or decimals. In these cases, you'll need to convert the numbers to a common denominator or whole numbers before attempting simplification. For instance, the ratio 0.5:1:1.5 can be converted to 1:2:3 by multiplying all numbers by 2.
Ratios and Proportions:
A proportion is a statement that equates two ratios. Proportions are extremely useful for solving problems where some values are unknown. The fundamental principle is that the product of the means (inner terms) equals the product of the extremes (outer terms). For example, in the proportion a/b = c/d, ad = bc.
Extending the Ratio Concept to More than Four Quantities:
The principle of simplifying ratios extends seamlessly to ratios with more than four quantities. You simply find the greatest common divisor of all the numbers and divide each number by the GCD. For example, to simplify the ratio 6:12:18:24, you would find the GCD (which is 6) and divide each number by 6, resulting in the simplified ratio 1:2:3:4.
Frequently Asked Questions (FAQ)
Q: Can I simplify a ratio by dividing only some of the numbers by a common factor?
A: No. You must divide all the numbers in the ratio by the same common factor (the GCD) to maintain the proportional relationships between the quantities. Dividing only some numbers will alter the ratios.
Q: What if the numbers in the ratio have no common factor other than 1?
A: If the greatest common divisor is 1, then the ratio is already in its simplest form. This was the case with our example of 3:4:1:6.
Q: Are there any online tools or calculators to simplify ratios?
A: While many online calculators can assist with finding the GCD, understanding the underlying mathematical process is key for broader application and problem-solving.
Q: How can I check if I've simplified a ratio correctly?
A: You can check your work by verifying that the simplified ratio is still proportional to the original ratio. This means you should be able to multiply each number in the simplified ratio by the same factor to obtain the original numbers.
Conclusion: Mastering Ratio Simplification
Mastering ratio simplification is not just about performing calculations; it's about understanding the fundamental principles of proportionality and applying them to solve real-world problems. The ratio 3:4:1:6, although already simplified, served as an excellent starting point to explore the concepts. Remember that finding the greatest common divisor is the cornerstone of this process, and always ensure you maintain the proportional relationship between the quantities throughout your calculations. With practice and a solid understanding of the underlying concepts, you'll confidently tackle even the most complex ratio problems. This knowledge will empower you to analyze data, solve problems, and apply these skills across various disciplines. Don't be afraid to practice – the more you work with ratios, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
Lcm Of 36 And 16
Sep 17, 2025
-
5 2 As A Fraction
Sep 17, 2025
-
What Percent Is 2 8
Sep 17, 2025
-
Gcf Of 80 And 20
Sep 17, 2025
-
4 To The 10 Power
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 4 1 6 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.