3 4 Divided By 3
saludintensiva
Sep 17, 2025 · 6 min read
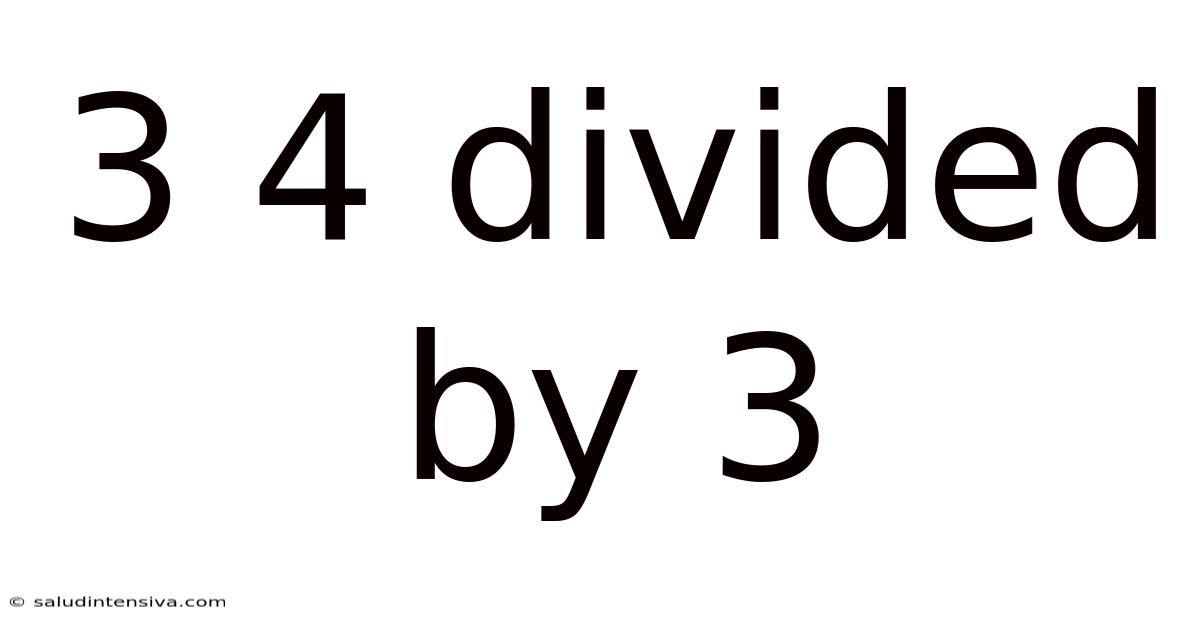
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/4 Divided by 3
This article explores the seemingly simple yet conceptually rich mathematical problem: 3/4 divided by 3. We'll dissect this calculation, moving beyond a mere answer to understand the underlying principles of fraction division. This will equip you with a solid grasp of fraction manipulation and empower you to tackle more complex problems with confidence. We'll cover various methods, from the traditional "invert and multiply" technique to visual representations, ensuring a comprehensive understanding for learners of all levels.
Understanding Fractions: A Quick Refresher
Before we dive into the division, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's composed of two key components: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4, meaning we have 3 out of 4 equal parts.
Method 1: The "Invert and Multiply" Method
This is the most common and efficient method for dividing fractions. The process involves three steps:
-
Invert the divisor: The divisor is the number you're dividing by. In our case, the divisor is 3 (or, more precisely, 3/1). Inverting a fraction means swapping the numerator and denominator. Inverting 3/1 gives us 1/3.
-
Change the division sign to a multiplication sign: Dividing by a fraction is equivalent to multiplying by its reciprocal (the inverted fraction). Therefore, our problem becomes: 3/4 x 1/3
-
Multiply the numerators and the denominators: To multiply fractions, we multiply the numerators together and the denominators together. This gives us: (3 x 1) / (4 x 3) = 3/12
-
Simplify the fraction: The fraction 3/12 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 3 and 12 is 3. Dividing both the numerator and denominator by 3, we get: 3/12 = 1/4
Therefore, 3/4 divided by 3 is 1/4.
Method 2: Visual Representation with Fraction Bars
Visualizing fractions can significantly aid understanding. Let's represent 3/4 using a fraction bar:
[Imagine a bar divided into four equal parts, with three of them shaded]
Now, we need to divide this shaded area (3/4) into three equal parts. To do this, we can further divide each of the four original parts into three smaller, equal parts. This results in a total of 12 smaller parts (4 x 3 = 12).
[Imagine the same bar now divided into twelve equal parts, with three of the original four parts still shaded. This would show 9 out of 12 parts shaded initially.]
We are dividing the initial shaded area (9/12, which simplifies to 3/4) into three equal groups. Each group will contain 3 out of the 12 smaller parts. This represents the fraction 3/12, which simplifies to 1/4.
This visual approach confirms our result obtained using the "invert and multiply" method.
Method 3: Understanding the Concept of Division
Division essentially asks: "How many times does one number fit into another?" When dividing fractions, we're asking how many times 3 fits into 3/4. Alternatively, we can ask: what fraction of 3/4 is equivalent to 1/3 of the whole?
This line of thinking reinforces the intuition behind the "invert and multiply" method. By inverting the divisor (3, or 3/1), we are essentially scaling the problem to find a solution in terms of the original fractional unit (1/4 in this case).
Why "Invert and Multiply" Works: A Deeper Look
The "invert and multiply" method isn't just a trick; it's a direct consequence of the definition of division and the properties of fractions. Consider the following:
-
Division as the inverse of multiplication: Dividing by a number is the same as multiplying by its reciprocal. This is a fundamental principle in mathematics.
-
Reciprocal of a fraction: The reciprocal of a fraction a/b is b/a. This is because (a/b) x (b/a) = 1. Multiplying a number by its reciprocal always equals 1.
-
Combining these principles: When we divide a fraction a/b by another fraction c/d, we are essentially solving the equation (a/b) / (c/d) = x. Multiplying both sides by (c/d), we get (a/b) = x(c/d). To solve for x, we multiply both sides by the reciprocal of (c/d), which is (d/c). This gives us x = (a/b) x (d/c). This demonstrates that dividing by a fraction is equivalent to multiplying by its reciprocal.
Expanding the Concept: Dividing Fractions by Whole Numbers and Vice-Versa
The principles discussed here extend to other scenarios:
-
Dividing a fraction by a whole number: Treat the whole number as a fraction with a denominator of 1 (e.g., 3 = 3/1). Then, apply the "invert and multiply" method.
-
Dividing a whole number by a fraction: Treat the whole number as a fraction with a denominator of 1. Again, apply the "invert and multiply" method.
For instance:
-
5 / (1/2) = 5/1 x 2/1 = 10
-
(2/3) / 4 = (2/3) / (4/1) = 2/3 x 1/4 = 2/12 = 1/6
Frequently Asked Questions (FAQs)
-
Why can't I just divide the numerator and denominator separately? You can only divide the numerator and denominator by the same number. Simply dividing the numerator (3) by the divisor (3) would give 1/4, which is incorrect. This method is only valid for simplifying fractions, not for dividing fractions.
-
What if the fraction is an improper fraction (numerator > denominator)? The "invert and multiply" method works equally well for improper fractions.
-
Are there other methods to divide fractions? Yes, other visual methods, such as using area models or circular representations, can be employed to illustrate the concept of fraction division, particularly for beginners. However, the invert-and-multiply method remains the most efficient and widely used technique.
-
How does this relate to real-world applications? Dividing fractions is crucial in numerous real-world situations, from measuring ingredients in cooking to calculating distances in construction and even understanding data analysis in various fields.
Conclusion
Dividing 3/4 by 3, resulting in 1/4, might seem trivial at first glance. However, understanding the underlying principles—the "invert and multiply" method, visual representations, and the conceptual meaning of division—is vital for mastering fraction manipulation. This knowledge extends far beyond this specific problem, enabling you to confidently tackle more complex fraction calculations and to build a strong foundation in mathematics. Remember that consistent practice and exploring various methods are key to developing a deep and intuitive understanding of this fundamental mathematical concept. Through understanding the mechanics and the reasoning behind fraction division, you'll become a more proficient and confident problem solver.
Latest Posts
Latest Posts
-
Scientific Notation And Significant Figures
Sep 18, 2025
-
Improper Fraction For 1 1 2
Sep 18, 2025
-
What Percent Is 11 12
Sep 18, 2025
-
Cuantas Libras Son 70 Kg
Sep 18, 2025
-
What Is 1 3 And 1 3
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.