3.5 5 As A Percent
saludintensiva
Sep 15, 2025 · 5 min read
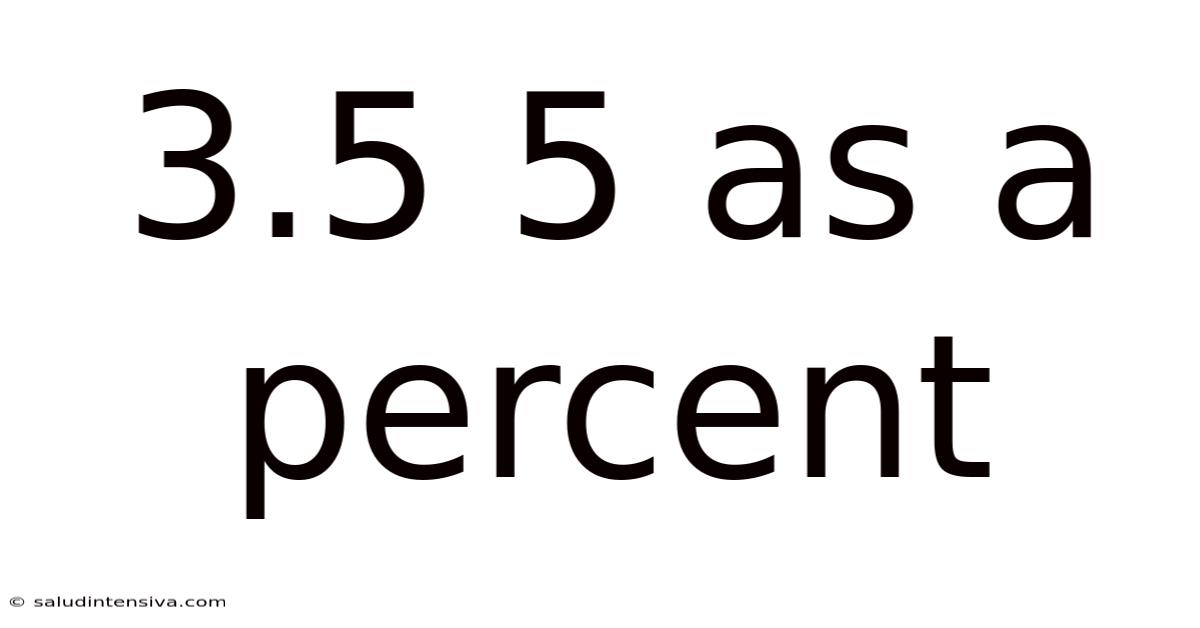
Table of Contents
Understanding 3.5/5 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in various fields, from calculating grades and discounts to understanding financial reports and statistical data. This comprehensive guide will delve into the process of converting the fraction 3.5/5 into a percentage, providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also explore the broader context of percentage calculations and their importance in everyday life.
Understanding Fractions and Percentages
Before diving into the conversion, let's solidify our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates how many parts out of 100 represent a given portion. For example, 50% means 50 out of 100, which simplifies to the fraction 1/2.
The key to converting a fraction to a percentage is to express the fraction as an equivalent fraction with a denominator of 100.
Converting 3.5/5 to a Percentage: A Step-by-Step Approach
The fraction 3.5/5 presents a slightly more complex scenario than a simple fraction with whole numbers. Let's break down the conversion process into manageable steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, divide the numerator by the denominator. In this case:
3.5 ÷ 5 = 0.7
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%).
0.7 x 100 = 70
Therefore, 0.7 is equivalent to 70%.
Step 3: Putting it all together
Combining the steps above, we can conclude that 3.5/5 is equal to 70%.
Alternative Method: Using Proportions
Another approach to solve this problem is by using proportions. We can set up a proportion to find the equivalent percentage:
3.5/5 = x/100
To solve for 'x' (the percentage), we can cross-multiply:
5x = 3.5 * 100
5x = 350
x = 350 ÷ 5
x = 70
Therefore, 3.5/5 is equal to 70%. This method reinforces the concept that a percentage is simply a fraction with a denominator of 100.
The Significance of Understanding Percentage Conversions
The ability to convert fractions to percentages is crucial for various reasons:
-
Interpreting Data: Many statistical reports, graphs, and charts use percentages to represent data. Understanding percentage conversions allows for accurate interpretation and comparison of data sets.
-
Financial Literacy: Percentages are essential for understanding interest rates, discounts, taxes, and other financial calculations. This understanding empowers individuals to make informed financial decisions.
-
Academic Performance: Grading systems often use percentages to represent academic performance. Converting fractional scores to percentages helps students understand their progress and identify areas needing improvement.
-
Real-world Applications: Percentages are used in numerous everyday situations, such as calculating tips, sales tax, or the percentage of ingredients in a recipe.
Beyond the Basics: Exploring More Complex Scenarios
While 3.5/5 represents a relatively straightforward conversion, let's consider some more complex scenarios that might arise:
-
Fractions with larger numbers: Converting fractions with significantly larger numerators and denominators requires careful calculation and potentially the use of a calculator. The principles remain the same: divide the numerator by the denominator to get the decimal, then multiply by 100 to get the percentage.
-
Improper fractions: An improper fraction has a numerator larger than its denominator (e.g., 7/5). When converting an improper fraction, the resulting percentage will be greater than 100%.
-
Mixed numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/2). To convert a mixed number to a percentage, first convert it into an improper fraction, then follow the steps outlined earlier.
Practical Applications and Examples
Let's explore some real-world examples where understanding 3.5/5 as 70% is beneficial:
-
Test Scores: If a student scores 3.5 out of 5 on a quiz, their percentage score is 70%. This allows for easy comparison with other students' scores.
-
Survey Results: If 3.5 out of 5 respondents agree with a statement in a survey, the percentage of agreement is 70%. This provides a clear representation of public opinion.
-
Discount Calculations: A 70% discount on an item means you pay only 30% of the original price. Understanding this conversion is crucial for smart shopping.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 3.5/5 to a percentage?
A: Yes, absolutely! Most calculators have a division function and can easily handle decimal calculations. Simply divide 3.5 by 5, then multiply the result by 100.
Q: What if the fraction involves more complex numbers?
A: The same principles apply. Divide the numerator by the denominator to obtain the decimal equivalent and then multiply by 100 to find the percentage. For very large numbers, a calculator is highly recommended.
Q: Why is understanding percentage conversions important?
A: Percentage conversions are fundamental to interpreting data, making financial decisions, understanding academic performance, and navigating numerous everyday situations.
Q: Are there any online tools to assist with percentage conversions?
A: While this article encourages understanding the process, many online calculators and converters are available to help with percentage calculations.
Conclusion
Converting 3.5/5 to a percentage (70%) is a simple yet fundamental mathematical operation with far-reaching applications. This guide has provided a clear, step-by-step explanation, explored alternative methods, and discussed the significance of understanding percentage conversions in various contexts. Mastering this skill empowers you to interpret data more effectively, make informed financial decisions, and confidently navigate numerous everyday situations that involve fractions and percentages. Remember the core principle: convert the fraction to a decimal, then multiply by 100 to obtain the equivalent percentage. This simple yet powerful skill is a cornerstone of mathematical literacy and practical problem-solving.
Latest Posts
Latest Posts
-
35 Percent Into A Fraction
Sep 15, 2025
-
1400 Degrees Celsius To Fahrenheit
Sep 15, 2025
-
How To Round Up 9
Sep 15, 2025
-
18 Cm Converted To Inches
Sep 15, 2025
-
What Is 9 12 Equal To
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3.5 5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.