3 5 In A Percent
saludintensiva
Sep 13, 2025 · 5 min read
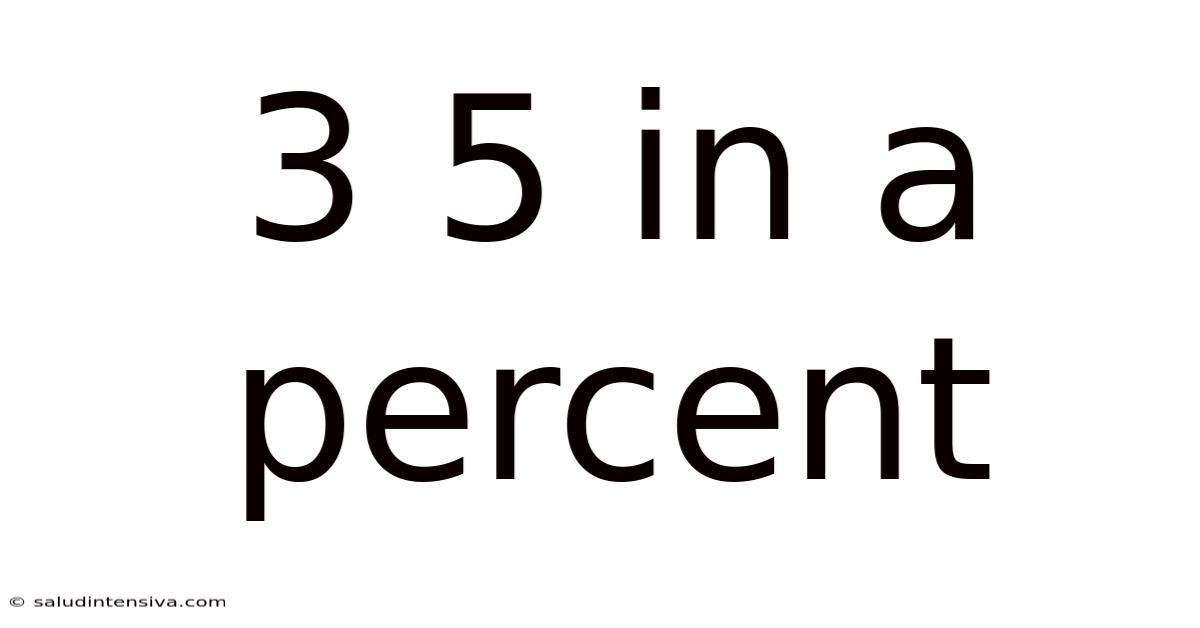
Table of Contents
Understanding 3.5% and its Applications: A Comprehensive Guide
What does 3.5% mean? It's a seemingly simple question, yet understanding percentages like 3.5% is crucial in various aspects of life, from finance and investments to everyday calculations. This article will delve deep into the meaning of 3.5%, exploring its practical applications, and providing you with the tools to confidently use it in different scenarios. We'll cover everything from basic calculations to more complex applications, ensuring you have a thorough understanding of this frequently encountered percentage.
What is 3.5%? A Percentage Breakdown
3.5% (3.5 percent) represents 3.5 parts out of every 100 parts. It's a fraction expressed as a proportion of 100. Just like any percentage, it can be easily converted to a decimal or a fraction to simplify calculations.
-
Decimal Form: To convert 3.5% to a decimal, simply divide by 100. This gives us 0.035.
-
Fraction Form: To express 3.5% as a fraction, we write it as 3.5/100. This can be simplified by multiplying both numerator and denominator by 10 to remove the decimal: 35/1000. This further simplifies to 7/200.
Calculating with 3.5%: Practical Examples
Let's explore how 3.5% is used in practical situations:
1. Calculating 3.5% of a Number:
This is a fundamental calculation. Let's say you want to find 3.5% of $5000. There are two ways to do this:
-
Method 1: Using the decimal form: Multiply the number by the decimal equivalent of 3.5%. So, $5000 * 0.035 = $175.
-
Method 2: Using the fraction form: Multiply the number by the fraction equivalent of 3.5%. So, $5000 * (7/200) = $175.
Both methods give the same result: 3.5% of $5000 is $175.
2. Finding the Original Value Given a Percentage:
Let's say you received a $175 bonus, which is 3.5% of your total salary. How can you calculate your total salary?
-
Use the following formula: Original Value = (Percentage Value / Percentage) * 100.
-
In this case: Original Salary = ($175 / 3.5) * 100 = $5000.
Therefore, your total salary is $5000.
3. Percentage Increase or Decrease:
Understanding 3.5% in the context of increases or decreases is vital in various applications, such as interest rates, inflation, or price changes.
-
Increase: If a price increases by 3.5%, you multiply the original price by 1.035. For example, if an item costs $100, a 3.5% increase would make it cost $100 * 1.035 = $103.50.
-
Decrease: If a price decreases by 3.5%, you multiply the original price by 0.965 (1 - 0.035). If an item costs $100, a 3.5% decrease would make it cost $100 * 0.965 = $96.50.
3.5% in Real-World Applications:
1. Finance and Investments:
-
Interest Rates: 3.5% is often seen as an interest rate on savings accounts, loans, or bonds. Understanding how this rate affects your savings or loan repayments is crucial for financial planning. A 3.5% annual interest rate means that for every $100 you have, you'll earn $3.50 in interest each year.
-
Investment Returns: If an investment provides a 3.5% return, this indicates the percentage increase in your investment's value over a specific period. It’s important to note that investment returns are not guaranteed and can fluctuate significantly.
-
Mortgage Rates: A 3.5% mortgage rate would significantly influence your monthly payments and the total cost of the mortgage over its lifespan. A lower interest rate translates into lower monthly payments and a lower total cost.
2. Sales and Discounts:
A 3.5% discount on a product indicates a reduction in the original price by 3.5%. For example, a 3.5% discount on a $200 item would reduce the price to $200 * 0.965 = $193.
3. Taxes and Fees:
Sales tax, property tax, or service fees are often expressed as percentages. Understanding the 3.5% tax on a purchase, for instance, allows you to calculate the total cost accurately.
4. Data Analysis and Statistics:
In data analysis, percentages are essential for interpreting data trends. A 3.5% change in a particular metric may indicate a significant trend or a minor fluctuation, depending on the context.
Understanding Compound Interest with 3.5%
Compound interest is the interest earned on both the principal amount and the accumulated interest from previous periods. Let's illustrate how 3.5% compound interest works over three years:
Let's say you invest $1000 at a 3.5% annual compound interest rate.
-
Year 1: $1000 * 0.035 = $35 interest earned. Your balance is now $1035.
-
Year 2: $1035 * 0.035 = $36.23 interest earned. Your balance is now $1071.23.
-
Year 3: $1071.23 * 0.035 = $37.49 interest earned. Your balance is now $1108.72.
Notice that the interest earned increases each year because the interest is calculated on an increasing balance. This demonstrates the power of compound interest over time. The longer the investment period, the more significant the effect of compounding.
Frequently Asked Questions (FAQ)
Q: How do I calculate 3.5% of a number without a calculator?
A: You can use the fraction form (7/200) to approximate the calculation. For larger numbers, it might be simpler to calculate 3% and 0.5% separately and add the results.
Q: What is the difference between simple and compound interest at 3.5%?
A: Simple interest is calculated only on the principal amount, while compound interest is calculated on both the principal and accumulated interest. Over time, compound interest yields significantly higher returns.
Q: Can 3.5% be expressed as a ratio?
A: Yes, 3.5% can be expressed as a ratio of 3.5:96.5 (3.5 parts to 96.5 parts). This represents the proportion of 3.5 parts out of a total of 100 parts.
Q: How does 3.5% relate to other percentages?
A: 3.5% is half of 7%, one-tenth of 35%, and one-hundredth of 350%. Understanding these relationships can help with quick mental calculations.
Conclusion: Mastering the Application of 3.5%
3.5%, while seemingly a small percentage, holds significant implications across numerous domains. Understanding its meaning, conversions, and applications in various calculations, especially concerning compound interest, is paramount for making informed decisions in finance, investments, and everyday life. By mastering these concepts, you'll equip yourself with the skills to confidently navigate situations involving this commonly used percentage. Remember, the key is to practice and apply these methods to different scenarios to solidify your understanding and build your confidence in handling percentages effectively. From calculating discounts to understanding investment returns, a firm grasp of 3.5% and percentage calculations in general is an invaluable asset.
Latest Posts
Latest Posts
-
Lcm Of 24 And 21
Sep 13, 2025
-
2 To The 3 Power
Sep 13, 2025
-
What Time Is 21 40
Sep 13, 2025
-
27 Out Of 30 Percentage
Sep 13, 2025
-
1 3 Divided By 4
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 5 In A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.