3 Out Of 7 Percentage
saludintensiva
Sep 14, 2025 · 6 min read
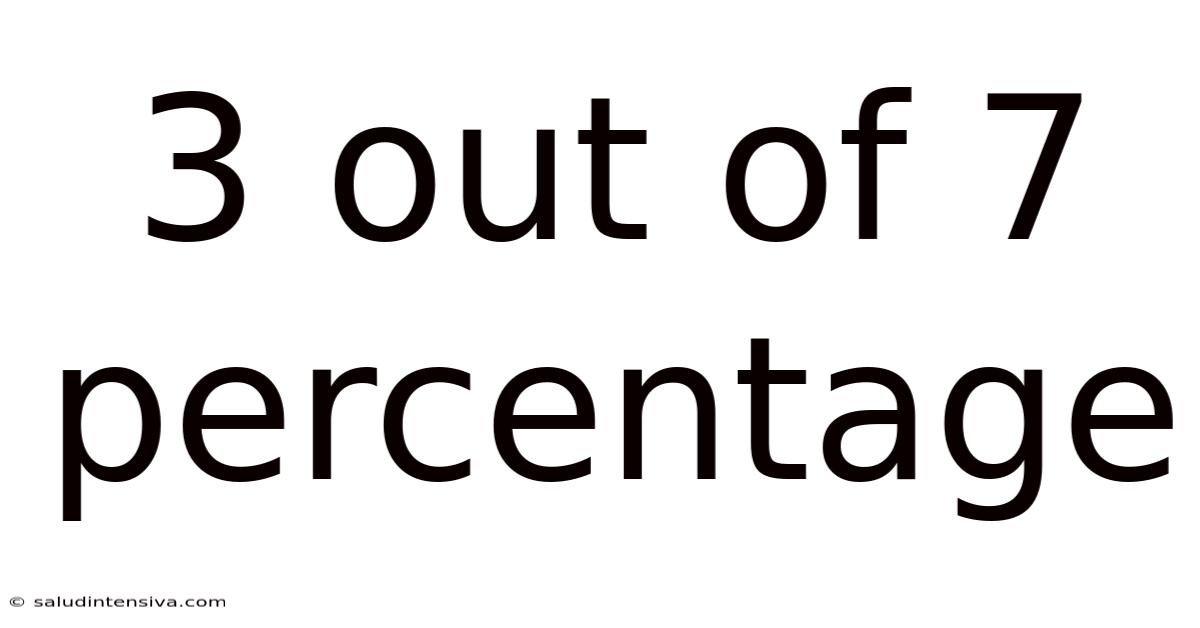
Table of Contents
Understanding 3 Out of 7: Percentages, Fractions, and Real-World Applications
Understanding percentages is a fundamental skill applicable in numerous aspects of daily life, from calculating discounts and sales tax to comprehending statistical data and evaluating investment returns. This article delves into the seemingly simple calculation of "3 out of 7," exploring its representation as a fraction, decimal, and percentage, and extending the discussion to encompass broader applications and related concepts. We will also touch upon how to solve similar problems and the importance of accurately interpreting such data.
Introduction: Framing the Problem
The phrase "3 out of 7" describes a ratio—a comparison of two quantities. It tells us that out of a total of 7 items or events, 3 possess a specific characteristic or meet a certain criterion. This ratio can be expressed in several ways: as a fraction, a decimal, and most importantly for practical applications, as a percentage. Mastering this conversion is key to comprehending its significance in various contexts.
Expressing 3 Out of 7 as a Fraction
The most straightforward representation of "3 out of 7" is a fraction: 3/7. The numerator (3) represents the number of items with the specific characteristic, while the denominator (7) represents the total number of items. This fraction is in its simplest form, meaning there's no common factor (other than 1) that can divide both the numerator and the denominator. This irreducibility makes it a precise representation of the ratio.
Converting the Fraction to a Decimal
To convert the fraction 3/7 to a decimal, we simply perform the division: 3 divided by 7. This results in a repeating decimal: approximately 0.428571428571... The sequence "428571" repeats indefinitely. For most practical purposes, rounding is necessary. Rounding to two decimal places, we get 0.43. The choice of the number of decimal places depends on the required level of precision for the specific application. A higher level of precision (more decimal places) provides a more accurate representation, but may be cumbersome in some instances.
Calculating the Percentage
Converting the decimal to a percentage involves multiplying by 100 and adding the "%" symbol. Using our rounded decimal of 0.43, we get: 0.43 * 100 = 43%. Therefore, "3 out of 7" is approximately 43%. It's crucial to understand that this is an approximation due to the rounding of the decimal. Using the full repeating decimal would provide a more precise percentage, though still an approximation because repeating decimals go on infinitely.
Understanding Percentage Accuracy: Precision vs. Practicality
The accuracy of a percentage calculation depends on the context. In some situations, an approximation (like 43%) is perfectly adequate. For instance, if you're discussing the percentage of students who passed a test, a rounded percentage is sufficient for general understanding. However, in other contexts, such as financial calculations or scientific measurements, greater precision is essential. In such cases, retaining more decimal places or using the fraction 3/7 directly might be necessary to avoid significant errors that could accumulate over multiple calculations.
Real-World Applications of Understanding 3/7
The ability to translate "3 out of 7" into different forms (fraction, decimal, percentage) is crucial in a variety of situations. Consider these examples:
- Sales and Marketing: A company might find that 3 out of 7 customers who saw a particular advertisement made a purchase. This 43% conversion rate is a vital metric for assessing the advertisement's effectiveness.
- Quality Control: If a factory produces 7 items, and 3 are defective, the defect rate is 43%. This information is essential for identifying and rectifying production issues.
- Scientific Research: In research involving statistical analysis, ratios like "3 out of 7" frequently arise. Converting this ratio to a percentage allows for easier comparison with other data sets.
- Everyday Life: Imagine you're baking a recipe that calls for 7 ingredients, and you've only acquired 3 so far. Knowing that you've obtained roughly 43% of the required ingredients can help with planning and shopping.
Solving Similar Problems: A Step-by-Step Guide
Let's generalize the process for solving problems similar to "3 out of 7":
- Identify the Part and the Whole: Determine the number representing the "part" (the number of items with the specific characteristic) and the number representing the "whole" (the total number of items).
- Formulate the Fraction: Create a fraction where the "part" is the numerator and the "whole" is the denominator. Simplify the fraction to its lowest terms if possible.
- Convert to Decimal: Divide the numerator by the denominator to obtain the decimal equivalent.
- Convert to Percentage: Multiply the decimal by 100 and add the "%" symbol. Round the percentage to the desired level of precision.
Example Problem: Calculating Success Rates
Let's say a student attempts 12 questions on a quiz and answers 9 correctly. What is their success rate as a percentage?
- Part: 9 (correct answers)
- Whole: 12 (total questions)
- Fraction: 9/12 = 3/4 (simplified)
- Decimal: 3 ÷ 4 = 0.75
- Percentage: 0.75 * 100 = 75%
The student achieved a 75% success rate on the quiz.
Further Exploration: Proportions and Ratios
Understanding "3 out of 7" extends beyond simple percentage calculations. It involves a broader understanding of proportions and ratios. A proportion is a statement that two ratios are equal. For example, 3/7 is proportional to 6/14 (both simplify to 3/7). Understanding proportions is crucial for solving problems involving scaling and comparing quantities.
Ratios, on the other hand, express the relative size of two or more values. The ratio of "3 out of 7" is often written as 3:7 or 3 to 7. Ratios are used extensively in various fields, including cooking (e.g., mixing ingredients in specific ratios), map scaling, and engineering design.
Frequently Asked Questions (FAQ)
Q: What if the numbers are larger? How do I calculate the percentage then?
A: The process remains the same. Regardless of the size of the numbers, you always follow the steps: create the fraction, convert to a decimal, and then to a percentage. A calculator can be particularly helpful with larger numbers.
Q: Is it always necessary to round the percentage?
A: Rounding is often necessary for practical purposes. However, in situations where high precision is required, rounding should be avoided or done to a sufficient number of decimal places to maintain accuracy.
Q: What if the "part" is larger than the "whole"?
A: This is not possible in a standard ratio. The "part" cannot be larger than the "whole." If such a situation arises, it indicates a potential error in data collection or interpretation.
Q: Can I use a calculator to solve these problems?
A: Absolutely! Calculators can be very helpful in converting fractions to decimals and decimals to percentages, especially when dealing with larger or more complex numbers.
Conclusion: The Power of Understanding Percentages
Mastering the concept of "3 out of 7," and its representation as a percentage, is more than just a mathematical skill. It’s a key component of critical thinking and data interpretation. By understanding how to convert ratios into percentages, you can effectively analyze data, make informed decisions, and confidently navigate various situations in your personal and professional life. Remember the key steps: find the fraction, convert to a decimal, and then calculate the percentage—and always consider the appropriate level of precision for your specific needs.
Latest Posts
Latest Posts
-
1 Sq Foot In Inches
Sep 14, 2025
-
300 Pounds How Many Kilos
Sep 14, 2025
-
1 1 4 2 3
Sep 14, 2025
-
Mulch Cost Per Cubic Yard
Sep 14, 2025
-
4 11 In Decimal Form
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 7 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.