31/4 As A Mixed Number
saludintensiva
Sep 21, 2025 · 6 min read
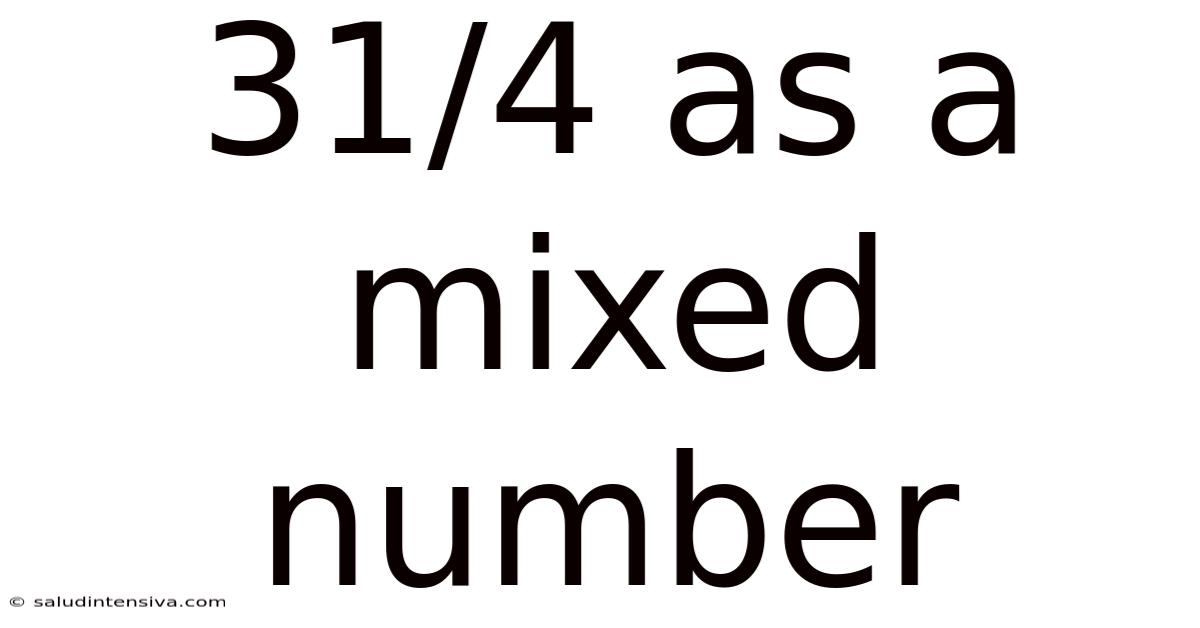
Table of Contents
Understanding 31/4 as a Mixed Number: A Comprehensive Guide
Fractions are fundamental building blocks in mathematics, representing parts of a whole. Understanding how to manipulate and interpret fractions is crucial for success in various mathematical disciplines. This comprehensive guide delves into the process of converting an improper fraction, like 31/4, into a mixed number, explaining the underlying principles and providing practical examples. We'll explore the concept of mixed numbers, the steps involved in the conversion, and address frequently asked questions to solidify your understanding. This article is designed for students, educators, and anyone seeking a deeper grasp of fractional arithmetic.
What are Mixed Numbers?
Before we dive into converting 31/4, let's clarify what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For instance, 1 ½ (one and a half) is a mixed number, where 1 is the whole number and ½ is the proper fraction. Mixed numbers are a convenient way to represent quantities that are greater than one but not a whole number.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. This indicates a value greater than or equal to one. The fraction 31/4 is an improper fraction because the numerator (31) is larger than the denominator (4). To convert an improper fraction to a mixed number, we need to determine how many times the denominator goes into the numerator and what the remainder is.
This process involves division. We divide the numerator by the denominator. The quotient (the result of the division) becomes the whole number part of the mixed number. The remainder becomes the numerator of the proper fraction, while the denominator remains the same.
Step-by-Step Conversion of 31/4
Let's apply this process to convert 31/4 into a mixed number:
-
Divide the numerator by the denominator: We divide 31 by 4.
31 ÷ 4 = 7 with a remainder of 3.
-
Identify the whole number: The quotient, 7, is the whole number part of our mixed number.
-
Identify the new numerator: The remainder, 3, becomes the numerator of the proper fraction.
-
Keep the original denominator: The denominator remains 4.
-
Combine the whole number and the proper fraction: This gives us the mixed number 7 ¾.
Therefore, 31/4 expressed as a mixed number is 7 ¾.
Visual Representation
Imagine you have 31 quarters (1/4). You can group these quarters into sets of four to make whole dollars. You can make 7 sets of four quarters (7 dollars), and you'll have 3 quarters left over. This visually represents the conversion: 7 whole dollars and 3/4 of a dollar, or 7 ¾.
Mathematical Explanation: The Division Algorithm
The conversion from an improper fraction to a mixed number is directly related to the division algorithm. The division algorithm states that for any integers a (dividend) and b (divisor) where b is not zero, there exist unique integers q (quotient) and r (remainder) such that:
a = bq + r, where 0 ≤ r < |b|
In our case, a = 31 (numerator), b = 4 (denominator). Performing the division, we find:
31 = 4 * 7 + 3
Here, q = 7 (the whole number) and r = 3 (the remainder, which becomes the numerator of the fraction). The denominator remains 4. This perfectly aligns with the steps outlined above.
Converting Mixed Numbers Back to Improper Fractions
It's important to understand the reverse process as well. To convert a mixed number back to an improper fraction, follow these steps:
-
Multiply the whole number by the denominator: In our example, 7 * 4 = 28.
-
Add the numerator to the result: 28 + 3 = 31.
-
Keep the original denominator: The denominator remains 4.
This gives us the improper fraction 31/4, confirming the accuracy of our initial conversion.
Applications of Mixed Numbers
Mixed numbers are frequently used in various real-world applications:
- Measurement: Measuring lengths, weights, or volumes often results in values expressed as mixed numbers (e.g., 2 ½ inches).
- Cooking: Recipes frequently use mixed numbers to specify quantities of ingredients (e.g., 1 ¾ cups of flour).
- Time: Time is often represented using mixed numbers (e.g., 2 ½ hours).
- Construction: Calculations involving dimensions and materials frequently use mixed numbers.
Understanding mixed numbers is therefore crucial for practical problem-solving in numerous fields.
Further Practice and Exploration
To solidify your understanding, try converting other improper fractions to mixed numbers. Consider fractions such as 25/6, 47/8, or 100/12. Practice converting these fractions, and then reverse the process to convert the resulting mixed numbers back into improper fractions. This will build your confidence and fluency in working with fractions.
Frequently Asked Questions (FAQ)
Q1: What happens if the remainder is zero?
A1: If the remainder is zero after dividing the numerator by the denominator, it means the improper fraction is actually a whole number. There is no fractional part. For example, 12/4 = 3.
Q2: Can I convert a mixed number with a negative whole number?
A2: Yes, you can. The process remains the same. For example, -2 ¾ can be converted to an improper fraction by multiplying the whole number (-2) by the denominator (4), adding the numerator (3), and keeping the denominator: (-8 + 3)/4 = -5/4.
Q3: Why is it important to learn about mixed numbers?
A3: Mixed numbers provide a more intuitive and user-friendly representation of quantities greater than one, making calculations and interpretations easier in practical contexts. They are essential for solving real-world problems in various fields.
Q4: Are there any other ways to represent fractions besides mixed numbers and improper fractions?
A4: Yes, decimals are another way to represent fractions. For example, 7 ¾ can be represented as 7.75. The choice of representation often depends on the context and the required level of precision.
Conclusion
Converting improper fractions, such as 31/4, into mixed numbers (7 ¾) is a fundamental skill in mathematics. This process, rooted in the division algorithm, simplifies the representation of quantities greater than one, enhancing both understanding and practical application. By mastering the conversion process and understanding the underlying principles, you will strengthen your foundation in fractional arithmetic and its various applications in the real world. Remember to practice regularly to build your skills and confidence in working with fractions. This will undoubtedly aid you in tackling more complex mathematical problems in the future.
Latest Posts
Latest Posts
-
90 Days From June 13
Sep 22, 2025
-
34 9 As A Mixed Number
Sep 22, 2025
-
2 8 Repeating As A Fraction
Sep 22, 2025
-
Images Of A Square Prism
Sep 22, 2025
-
Ratio Word Problems 7th Grade
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 31/4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.