35 Percent As A Fraction
saludintensiva
Sep 12, 2025 · 5 min read
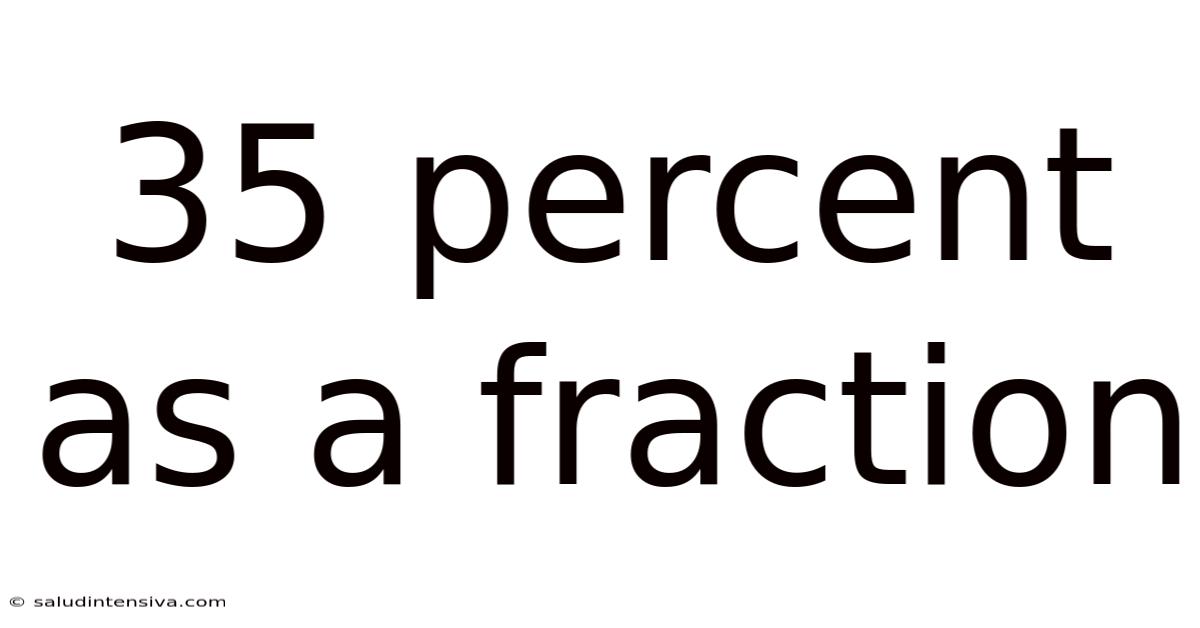
Table of Contents
35 Percent as a Fraction: A Comprehensive Guide
Understanding percentages and their fractional equivalents is a fundamental skill in mathematics, crucial for various applications from everyday budgeting to advanced scientific calculations. This comprehensive guide will explore the conversion of 35 percent into a fraction, delve into the underlying principles of percentage-to-fraction conversion, and offer practical examples to solidify your understanding. We'll also address common misconceptions and frequently asked questions.
Understanding Percentages and Fractions
Before we tackle the conversion of 35%, let's refresh our understanding of percentages and fractions. A percentage represents a fraction of 100. The word "percent" literally means "per hundred." Therefore, 35% means 35 out of 100. A fraction, on the other hand, expresses a part of a whole, represented by a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of parts, while the numerator indicates the number of parts being considered.
Converting 35% to a Fraction: The Simple Method
The simplest way to convert 35% to a fraction is to remember its literal meaning: 35 out of 100. This directly translates into the fraction 35/100.
This fraction, however, can be simplified. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 35 and 100 is 5. Dividing both the numerator and the denominator by 5, we get:
35 ÷ 5 = 7 100 ÷ 5 = 20
Therefore, the simplified fraction equivalent of 35% is 7/20.
Step-by-Step Guide to Converting Percentages to Fractions
The process of converting any percentage to a fraction can be broken down into these simple steps:
-
Write the percentage as a fraction with a denominator of 100: For example, 35% becomes 35/100. This step directly reflects the definition of percentage.
-
Simplify the fraction: Find the greatest common divisor (GCD) of the numerator and the denominator. Divide both the numerator and the denominator by the GCD. This reduces the fraction to its simplest form. If you're unsure how to find the GCD, you can use the Euclidean algorithm or simply list the factors of both numbers to find the largest common factor.
-
Check your answer: Ensure the resulting fraction is in its simplest form; no common factors should exist between the numerator and denominator besides 1.
Applying the Process to Other Percentages
Let's practice converting other percentages to fractions using the steps outlined above:
- 20%: 20/100 simplifies to 1/5
- 60%: 60/100 simplifies to 3/5
- 75%: 75/100 simplifies to 3/4
- 12.5%: 12.5/100 simplifies to 1/8 (This involves multiplying both numerator and denominator by 2 to remove the decimal)
- 150%: 150/100 simplifies to 3/2 (This results in an improper fraction, where the numerator is larger than the denominator)
Dealing with Decimals in Percentages
When dealing with percentages containing decimals, such as 12.5%, the process remains similar, but an extra step is usually required to remove the decimal. Multiply both the numerator and the denominator by a power of 10 (10, 100, 1000, etc.) to make the numerator a whole number. In the example of 12.5%, multiplying both by 10 gives us 125/1000, which simplifies to 1/8.
Understanding Improper Fractions
Sometimes, converting a percentage greater than 100% will result in an improper fraction, where the numerator is larger than the denominator. This simply means that the fraction represents a quantity greater than one whole. For instance, 150% converts to 150/100, which simplifies to 3/2. This improper fraction can be converted into a mixed number (1 1/2) to represent 1 whole and 1/2.
Mathematical Applications of Percentage-to-Fraction Conversions
The ability to convert percentages to fractions is crucial in various mathematical contexts:
-
Probability and Statistics: Percentages are often used to express probabilities, and converting them to fractions is essential for many calculations in probability theory.
-
Algebra: Many algebraic problems involve fractions, and understanding how to represent percentages as fractions allows for seamless integration in solving these equations.
-
Geometry: Calculations involving area, volume, and proportions frequently use fractions, requiring the ability to convert percentages appropriately.
-
Finance and Business: Percentage calculations are ubiquitous in financial applications, ranging from interest rates to profit margins, and understanding their fractional equivalents is paramount.
Common Misconceptions and Errors
One common mistake is forgetting to simplify the fraction after converting the percentage. Always ensure the fraction is in its lowest terms by finding the GCD and dividing accordingly. Another error stems from misinterpreting the meaning of percentage. Remember that a percentage is always a fraction of 100.
Frequently Asked Questions (FAQ)
-
Q: Can all percentages be converted to fractions? A: Yes, any percentage can be represented as a fraction with a denominator of 100.
-
Q: What if I get a very large fraction after the initial conversion? A: Simplify it! Finding the GCD and reducing the fraction will result in a much more manageable number.
-
Q: How do I convert a fraction back into a percentage? A: Divide the numerator by the denominator and multiply the result by 100.
-
Q: Are there any shortcuts for converting certain percentages? A: Yes, for commonly used percentages like 25%, 50%, and 75%, you can often recognize the simplified fractions directly.
-
Q: Why is it important to know how to convert percentages to fractions? A: It's crucial for a strong foundation in mathematics, allowing for easier manipulation and calculations in various fields.
Conclusion
Converting 35% to a fraction, which simplifies to 7/20, is a straightforward process that highlights the fundamental connection between percentages and fractions. Mastering this conversion is essential for anyone aiming to improve their mathematical skills and understanding. By following the step-by-step guide and practicing with different percentages, you can confidently navigate this crucial aspect of mathematics and apply it to numerous real-world scenarios. Remember to always simplify your fractions to their lowest terms for the most accurate and efficient representation. Through understanding these concepts, you'll not only solve problems effectively but also develop a deeper appreciation for the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
Convert 25 F To C
Sep 12, 2025
-
Whats 10 Percent Of 5
Sep 12, 2025
-
0 25 Acre To Sq Ft
Sep 12, 2025
-
Is 247 A Prime Number
Sep 12, 2025
-
Gcf Of 50 And 80
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 35 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.