Whats 10 Percent Of 5
saludintensiva
Sep 12, 2025 · 6 min read
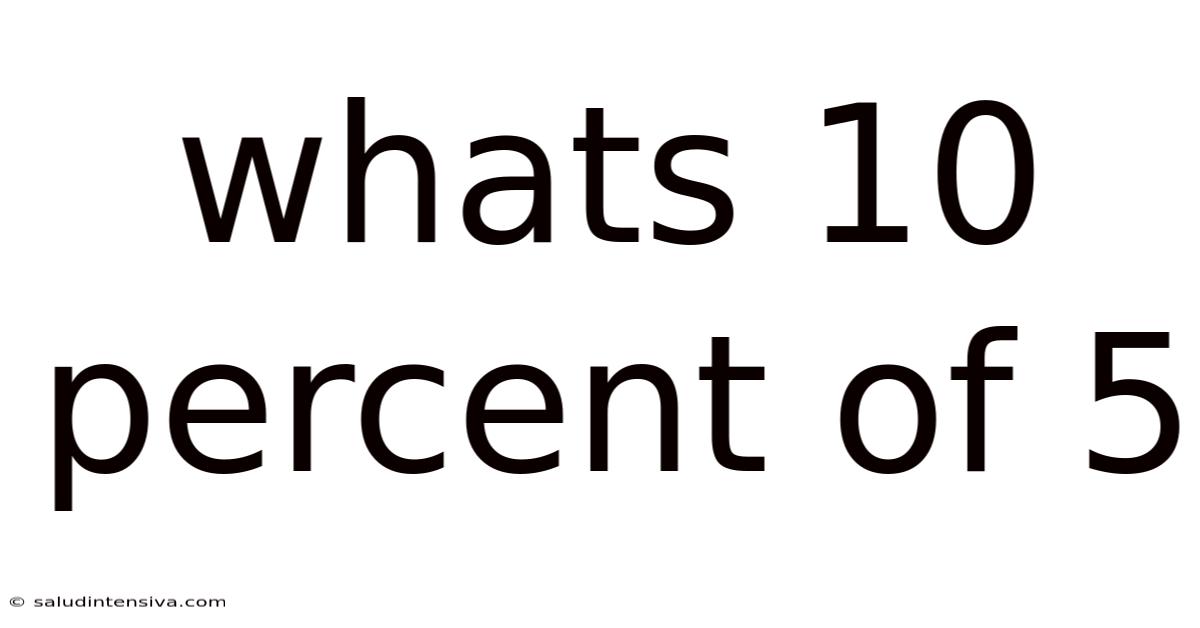
Table of Contents
What's 10 Percent of 5? A Deep Dive into Percentages and Their Applications
Finding 10 percent of 5 might seem like a simple calculation, readily solved with a quick mental computation or a calculator. However, understanding the underlying principles of percentages opens doors to a broader comprehension of mathematical concepts crucial in everyday life, from calculating discounts and tips to understanding financial reports and statistical analyses. This article will not only answer the question "What's 10 percent of 5?" but also explore the broader context of percentages, their applications, and how to approach similar problems confidently.
Understanding Percentages: A Foundation
A percentage is a fraction or a ratio expressed as a part of 100. The term "percent" is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 10 percent means 10 out of 100, or 10/100, which simplifies to 1/10. This foundational understanding is key to solving percentage problems. Think of it like dividing something into 100 equal pieces; a percentage tells you how many of those pieces you have.
Calculating 10 Percent of 5: The Simple Method
The simplest method to calculate 10 percent of 5 involves directly applying the definition of percentage. Since 10 percent is equivalent to 1/10, we can calculate 10 percent of 5 by multiplying 5 by 1/10:
5 * (1/10) = 5/10 = 0.5
Therefore, 10 percent of 5 is 0.5.
Calculating 10 Percent of 5: The Decimal Method
Another common approach involves converting the percentage to its decimal equivalent. To do this, we divide the percentage by 100. In this case, 10 percent becomes 10/100 = 0.1. Then, we multiply this decimal by the number we're interested in:
5 * 0.1 = 0.5
Again, we arrive at the same answer: 10 percent of 5 is 0.5. This method is particularly useful when dealing with percentages that aren't easily converted to simple fractions.
Beyond the Basics: Applying Percentage Calculations
While finding 10 percent of 5 is straightforward, understanding the broader applications of percentage calculations is crucial. Here are some real-world scenarios where these skills come in handy:
-
Sales and Discounts: Retailers frequently offer discounts expressed as percentages. For instance, a "20% off" sale means you pay 80% of the original price. Understanding percentage calculations allows you to quickly determine the final price after a discount.
-
Taxes: Sales taxes, income taxes, and other taxes are usually expressed as percentages. Knowing how to calculate percentages helps you understand the total cost of an item, including taxes, and manage your finances effectively.
-
Tips and Gratuities: When dining out or receiving services, calculating tips is often based on a percentage of the bill. This requires accurate percentage calculations to ensure fair compensation.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentage calculations is essential for comprehending the growth or cost associated with these financial instruments.
-
Statistical Analysis: Percentages are frequently used in statistical analysis to represent proportions, probabilities, and changes in data. Understanding percentages allows for better interpretation of data and informed decision-making.
-
Financial Reports: Financial statements, such as balance sheets and income statements, often use percentages to show ratios and trends. Understanding percentages is critical for interpreting financial performance and making sound investment decisions.
Solving More Complex Percentage Problems: A Step-by-Step Guide
Let's explore how to tackle more challenging percentage problems. The key lies in breaking down the problem into manageable steps:
1. Identify the Key Elements: Determine the base value (the number you're finding a percentage of), the percentage rate, and the unknown value (what you're trying to find).
2. Convert the Percentage to a Decimal: Divide the percentage by 100.
3. Multiply: Multiply the base value by the decimal equivalent of the percentage.
4. Solve: This will give you the answer.
Example: What is 25% of 80?
-
Key Elements: Base value = 80, Percentage rate = 25%, Unknown value = ?
-
Convert to Decimal: 25% / 100 = 0.25
-
Multiply: 80 * 0.25 = 20
-
Solve: 25% of 80 is 20.
Finding the Percentage: A Reverse Calculation
Sometimes, you need to determine the percentage one value represents of another. For instance, if you scored 15 out of 20 on a test, what is your percentage score? Follow these steps:
-
Divide: Divide the part by the whole (15/20 = 0.75).
-
Multiply by 100: Multiply the result by 100 to express it as a percentage (0.75 * 100 = 75%).
Therefore, a score of 15 out of 20 represents a 75% score.
Understanding Percentage Increase and Decrease
Percentages are also used to represent increases or decreases. For example, a 10% increase means adding 10% of the original value to the original value, while a 10% decrease means subtracting 10% of the original value from the original value.
Example (Increase): A price increases by 15%. The original price is $50.
-
Calculate the increase: 15% of $50 = 0.15 * $50 = $7.50
-
Add the increase to the original value: $50 + $7.50 = $57.50
The new price is $57.50.
Example (Decrease): A population decreases by 5%. The original population is 1000.
-
Calculate the decrease: 5% of 1000 = 0.05 * 1000 = 50
-
Subtract the decrease from the original value: 1000 - 50 = 950
The new population is 950.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage of a number without a calculator?
A: You can use the fraction method, converting the percentage to a fraction and simplifying before multiplication. For example, 20% of 60 is (20/100) * 60 = (1/5) * 60 = 12.
-
Q: What if the percentage is a decimal, like 2.5%?
A: Convert the decimal percentage to a decimal number by dividing by 100 (2.5% = 0.025) and then multiply by the base value.
-
Q: How can I improve my skills in percentage calculations?
A: Practice regularly with various problems. Start with simpler problems and gradually increase the complexity. Use online resources, workbooks, and real-world scenarios to hone your skills.
Conclusion: Mastering Percentages for Real-World Success
This article started with the seemingly simple question: "What's 10 percent of 5?" However, the journey beyond this initial calculation has revealed the wide-ranging applicability and importance of understanding percentages. From navigating sales and discounts to interpreting financial reports and understanding statistical data, mastery of percentage calculations is a fundamental skill for success in various aspects of life. By understanding the underlying principles and applying the methods outlined, you can confidently approach percentage problems and unlock a deeper understanding of the mathematical world around you. Remember that consistent practice is key to mastering this essential skill.
Latest Posts
Latest Posts
-
Convert 15 Into A Decimal
Sep 12, 2025
-
Equivalent Fraction Of 3 12
Sep 12, 2025
-
Is 87 Composite Or Prime
Sep 12, 2025
-
What Is Half Of 17
Sep 12, 2025
-
Lcm Of 10 And 40
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 10 Percent Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.