Lcm Of 10 And 40
saludintensiva
Sep 12, 2025 · 6 min read
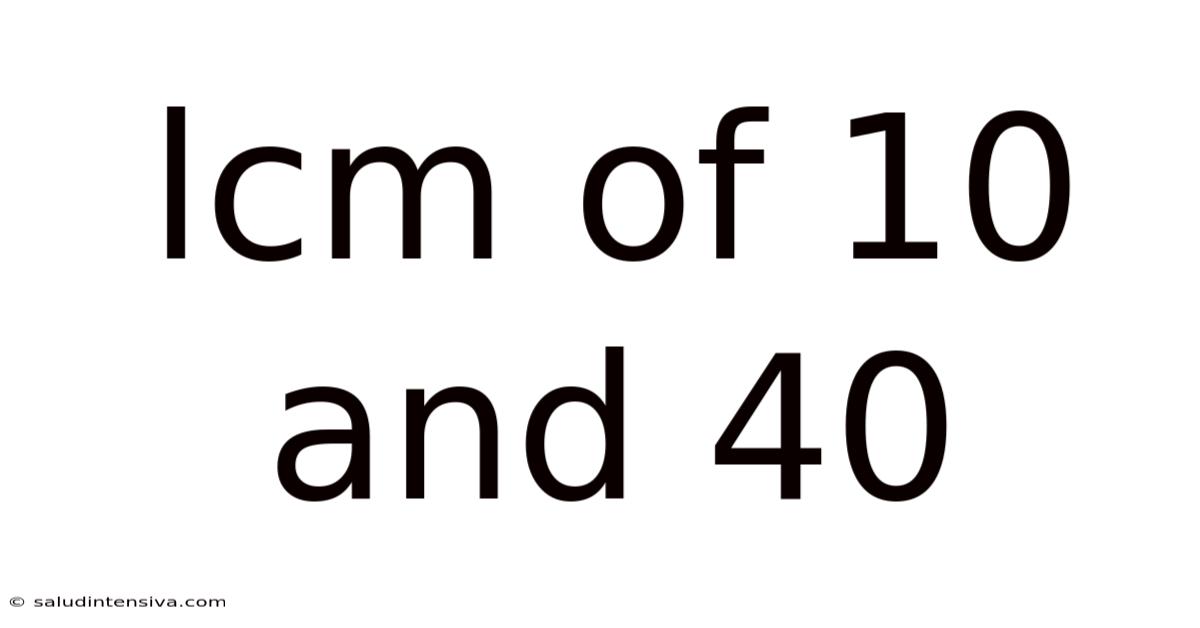
Table of Contents
Finding the LCM of 10 and 40: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in areas like fractions, ratios, and solving real-world problems involving cycles or repetitions. This comprehensive guide will delve into the various methods for calculating the LCM of 10 and 40, explaining the underlying principles and demonstrating practical applications. We'll explore different approaches, from simple listing multiples to using prime factorization and the greatest common divisor (GCD), ensuring a thorough understanding for learners of all levels.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more numbers is the smallest positive integer that is divisible by all the numbers. Think of it as the smallest number that contains all the numbers as factors. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14...
- Multiples of 3: 3, 6, 9, 12, 15, 18...
The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6. This concept becomes increasingly important when dealing with more complex numbers and operations, especially when working with fractions.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. Let's apply it to find the LCM of 10 and 40:
-
List the multiples of 10: 10, 20, 30, 40, 50, 60, 70...
-
List the multiples of 40: 40, 80, 120, 160...
-
Identify the smallest common multiple: Observe that 40 is the smallest number present in both lists.
Therefore, the LCM of 10 and 40 is 40. This method is simple but can become time-consuming and impractical for larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Find the prime factorization of 10: 10 = 2 x 5
-
Find the prime factorization of 40: 40 = 2 x 2 x 2 x 5 = 2³ x 5
-
Identify the highest power of each prime factor: The prime factors present are 2 and 5. The highest power of 2 is 2³ (or 8) and the highest power of 5 is 5¹.
-
Multiply the highest powers together: LCM(10, 40) = 2³ x 5 = 8 x 5 = 40
Therefore, the LCM of 10 and 40 using prime factorization is 40. This method is generally preferred for its efficiency and applicability to larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The GCD, or greatest common divisor, is the largest number that divides both numbers without leaving a remainder. There's a useful relationship between the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Let's use this relationship to find the LCM of 10 and 40:
-
Find the GCD of 10 and 40: The factors of 10 are 1, 2, 5, 10. The factors of 40 are 1, 2, 4, 5, 8, 10, 20, 40. The greatest common factor is 10. Therefore, GCD(10, 40) = 10.
-
Apply the LCM-GCD relationship: LCM(10, 40) x GCD(10, 40) = 10 x 40
-
Solve for LCM: LCM(10, 40) = (10 x 40) / GCD(10, 40) = (10 x 40) / 10 = 40
Therefore, the LCM of 10 and 40 using the GCD method is 40. This method is particularly useful when dealing with larger numbers where finding prime factors might be more challenging.
Practical Applications of LCM
The LCM has many real-world applications, including:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 10 minutes, and the other every 40 minutes. The LCM (40 minutes) tells us when both buses will arrive simultaneously again.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. For example, adding 1/10 and 1/40 requires finding the LCM of 10 and 40, which is 40. This allows us to rewrite the fractions as 4/40 + 1/40 = 5/40, which can then be simplified.
-
Cyclic Events: In scenarios involving repeating cycles or patterns, the LCM helps determine when these cycles will align. For example, if two machines have different operating cycles, the LCM helps predict when maintenance needs to be performed on both simultaneously.
-
Measurement Conversion: The LCM can be useful when converting between different units of measurement that have a common factor.
Frequently Asked Questions (FAQ)
-
What if one number is a multiple of the other? If one number is a multiple of the other (as in this case, 40 is a multiple of 10), the larger number is the LCM.
-
Can the LCM be greater than both numbers? Yes, the LCM can be greater than both numbers, especially when the numbers don't share any common factors other than 1.
-
Is there a formula for LCM? While there isn't a single, universal formula, the relationship between LCM and GCD provides a powerful method for calculating the LCM: LCM(a, b) = (a x b) / GCD(a, b).
-
How can I find the LCM of more than two numbers? You can extend the prime factorization method or the GCD-based method to find the LCM of multiple numbers. For prime factorization, you find the highest power of each prime factor present in all the numbers. For the GCD method, you would iteratively find the LCM of pairs of numbers.
-
Are there any online calculators for LCM? Yes, many online calculators can compute the LCM of numbers quickly and efficiently. However, understanding the underlying methods is crucial for solving problems involving LCM in various contexts.
Conclusion
Finding the LCM of 10 and 40, as demonstrated through multiple methods, highlights the importance of understanding fundamental mathematical concepts. The straightforward listing method is suitable for smaller numbers, while prime factorization and the GCD method offer more efficient and versatile approaches for larger numbers and more complex problems. Understanding the LCM is essential not only for academic success but also for solving practical problems in various fields, from scheduling to fraction arithmetic. Mastering this concept provides a strong foundation for tackling more advanced mathematical challenges. The ability to choose the most appropriate method depending on the context is a valuable skill that will enhance your mathematical problem-solving capabilities significantly. Remember to always choose the method that you find most comfortable and efficient for the given task. Practice is key to mastering these techniques.
Latest Posts
Latest Posts
-
How Long Is 700 Minutes
Sep 12, 2025
-
Is 119 A Prime Number
Sep 12, 2025
-
Lcm Of 8 And 2
Sep 12, 2025
-
1 1 4 In Inches
Sep 12, 2025
-
1 1 8 X 3
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.