39 50 As A Decimal
saludintensiva
Sep 18, 2025 · 5 min read
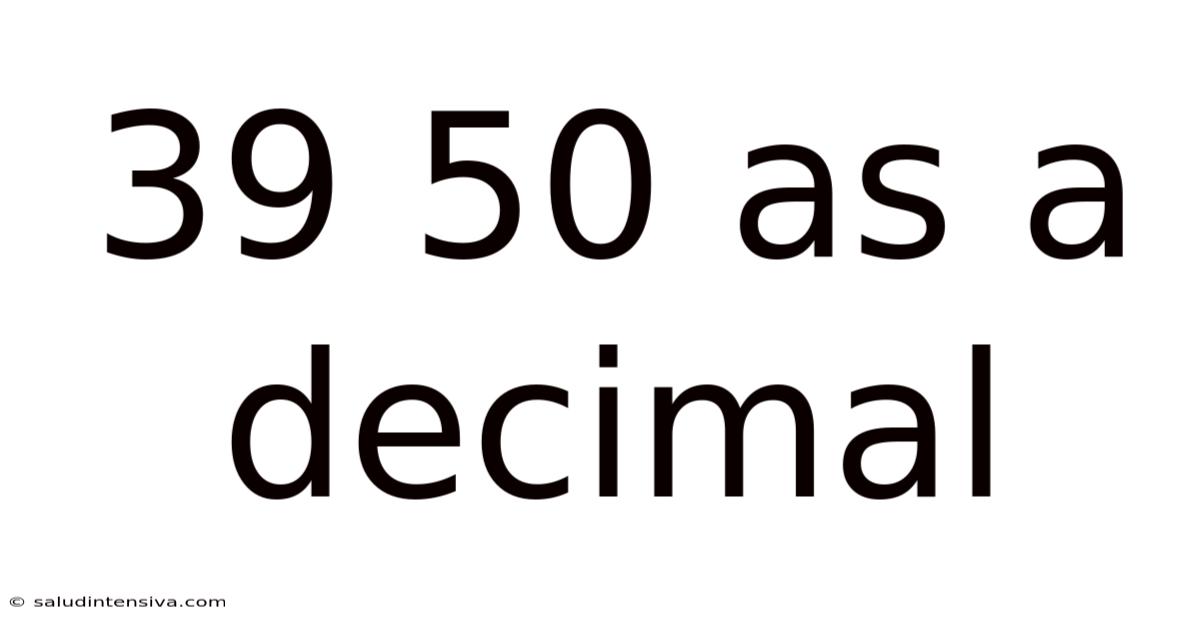
Table of Contents
Decoding 39/50 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics and numerous real-world applications. This article will delve deep into converting the fraction 39/50 into its decimal form, exploring various methods, explaining the underlying principles, and addressing common questions. We'll also explore the broader context of fraction-to-decimal conversion, demonstrating its practical relevance. By the end, you'll not only know the decimal equivalent of 39/50 but also possess a solid understanding of the process and its applications.
Understanding Fractions and Decimals
Before we tackle the conversion of 39/50, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 39/50, 39 represents the number of parts we have, and 50 represents the total number of equal parts in the whole.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). Decimals are written using a decimal point (.), separating the whole number part from the fractional part. For example, 0.75 represents 75/100.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. We divide the numerator (39) by the denominator (50).
39 ÷ 50 = 0.78
Therefore, the decimal equivalent of 39/50 is 0.78. This method is simple and easily performed using a calculator or long division. Long division involves systematically dividing the numerator by the denominator, placing the decimal point appropriately, and adding zeros as needed to continue the division until a remainder of zero is achieved or a repeating pattern emerges.
Method 2: Converting to an Equivalent Fraction with a Denominator of 100
Another approach involves converting the given fraction into an equivalent fraction with a denominator of 100. This method is particularly useful when the denominator is a factor of 100 or a simple multiple thereof.
Since 50 is a factor of 100 (100 ÷ 50 = 2), we can multiply both the numerator and the denominator of 39/50 by 2 to obtain an equivalent fraction with a denominator of 100:
(39 × 2) / (50 × 2) = 78/100
Now, we can easily express 78/100 as a decimal: 0.78. This method provides a visual representation of the fraction's value in terms of hundredths, which can be helpful for understanding percentages and decimal place value.
Method 3: Using Percentages
Percentages are closely related to decimals and fractions. A percentage represents a fraction where the denominator is 100. To convert a fraction to a percentage, we first express the fraction as a decimal and then multiply by 100%.
As we have already established, 39/50 = 0.78. Multiplying this decimal by 100% gives us:
0.78 × 100% = 78%
This shows that 39/50 is equivalent to 78%, which further reinforces the understanding of its decimal representation. Converting to a percentage can be particularly useful when dealing with proportions and ratios in various contexts, such as financial calculations or statistical analysis.
Understanding the Decimal Place Value
The decimal representation 0.78 consists of two digits after the decimal point. The digit 7 represents seven-tenths (7/10), and the digit 8 represents eight-hundredths (8/100). Understanding place value is crucial for interpreting and working with decimals. Each position to the right of the decimal point represents a decreasing power of 10.
Practical Applications of Fraction-to-Decimal Conversion
The ability to convert fractions to decimals is crucial in various real-world scenarios:
- Financial Calculations: Interest rates, discounts, and tax calculations often involve fractions that need to be converted to decimals for accurate computation.
- Measurement and Engineering: Precise measurements in fields like engineering and construction frequently require converting fractions to decimals for calculations and design specifications.
- Data Analysis and Statistics: Working with data often involves expressing proportions and frequencies as decimals for easier statistical analysis and interpretation.
- Scientific Calculations: Many scientific formulas and calculations require the use of decimals for precise results.
- Everyday Life: Many everyday situations, such as sharing food or calculating distances, can involve fractions that need conversion to decimals for practical applications.
Addressing Common Questions and Misconceptions
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that are not factors of powers of 10 (i.e., denominators containing prime factors other than 2 and 5) will result in non-terminating, repeating decimals. For example, 1/3 converts to 0.3333...
Q: What is the difference between a terminating and a repeating decimal?
A: A terminating decimal has a finite number of digits after the decimal point, while a repeating decimal has a pattern of digits that repeats infinitely.
Q: How do I handle fractions with larger numerators and denominators?
A: The same methods (direct division, equivalent fractions, etc.) apply, though the calculations may be more complex. Using a calculator is often helpful for larger numbers.
Q: Is there a shortcut for converting fractions with a denominator of 50?
A: Yes, as demonstrated earlier, you can easily multiply both the numerator and denominator by 2 to obtain an equivalent fraction with a denominator of 100, making conversion to a decimal straightforward.
Conclusion
Converting the fraction 39/50 to its decimal equivalent, 0.78, is a simple yet fundamental mathematical skill with wide-ranging applications. Through direct division, equivalent fraction conversion, or the use of percentages, the decimal representation can be easily obtained. Understanding the underlying principles of fractions, decimals, and place value is crucial for proficiency in mathematics and successful navigation of various real-world situations that involve fractional values. This knowledge forms a strong foundation for more advanced mathematical concepts and problem-solving. Mastering this skill opens doors to more complex mathematical explorations and a deeper appreciation of numerical relationships.
Latest Posts
Latest Posts
-
Random Number Generator 0 99
Sep 18, 2025
-
60 Days From 1 15
Sep 18, 2025
-
First 6 Multiples Of 5
Sep 18, 2025
-
5 1 4 2 3 4
Sep 18, 2025
-
When Was 29 Weeks Ago
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 39 50 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.