5 1/4 - 2 3/4
saludintensiva
Sep 18, 2025 · 6 min read
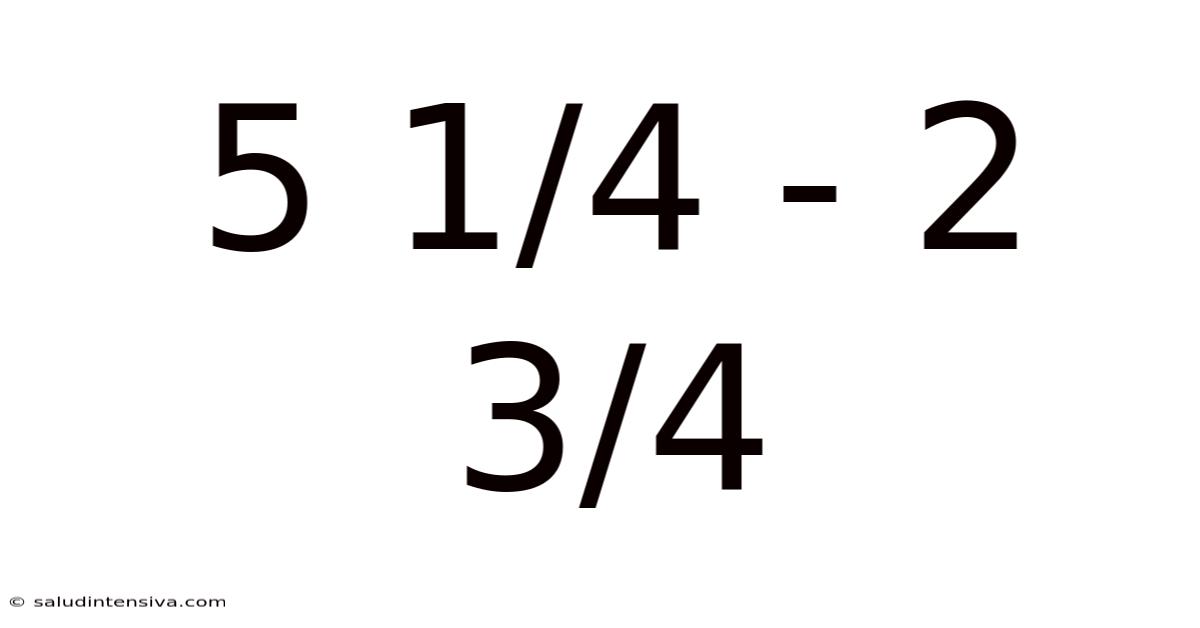
Table of Contents
Mastering Subtraction of Mixed Numbers: A Deep Dive into 5 1/4 - 2 3/4
Subtracting mixed numbers might seem daunting at first, but with a structured approach and a solid understanding of fractions, it becomes a manageable and even enjoyable mathematical skill. This comprehensive guide will walk you through the process of subtracting 5 1/4 - 2 3/4, explaining the steps, providing the solution, and exploring the underlying mathematical principles. We'll also delve into common errors and offer helpful tips to ensure your success in tackling similar problems. This article will equip you with the confidence to solve any mixed number subtraction problem you encounter.
Introduction: Understanding Mixed Numbers and Subtraction
A mixed number combines a whole number and a fraction. For instance, 5 1/4 represents 5 whole units and an additional 1/4 of a unit. Subtracting mixed numbers involves subtracting both the whole number parts and the fractional parts separately. However, the process isn't always as straightforward as it seems. Sometimes, we encounter situations where the fraction in the subtrahend (the number being subtracted) is larger than the fraction in the minuend (the number from which we're subtracting). This is precisely the challenge we face with 5 1/4 - 2 3/4, as 3/4 is greater than 1/4.
Step-by-Step Solution: 5 1/4 - 2 3/4
-
Analyze the Fractions: Notice that 1/4 is smaller than 3/4. This means we cannot directly subtract the fractions. We need to borrow from the whole number part of the minuend.
-
Borrowing from the Whole Number: We borrow 1 from the whole number 5, leaving us with 4. This borrowed 1 is then converted into a fraction with the same denominator as the existing fractions (4). Therefore, 1 becomes 4/4.
-
Rewrite the Minuend: Our minuend, 5 1/4, is now rewritten as 4 + 4/4 + 1/4 = 4 5/4.
-
Subtract the Whole Numbers: Now we subtract the whole numbers: 4 - 2 = 2.
-
Subtract the Fractions: Next, we subtract the fractions: 5/4 - 3/4 = 2/4.
-
Combine the Results: Finally, we combine the results of the whole number subtraction and the fraction subtraction: 2 + 2/4 = 2 2/4.
-
Simplify the Fraction (if necessary): The fraction 2/4 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2. Therefore, 2/4 simplifies to 1/2.
-
Final Answer: The final answer to 5 1/4 - 2 3/4 is 2 1/2.
Detailed Explanation of Borrowing
The borrowing step is crucial and often the source of confusion. Let's break down why it works:
Imagine you have 5 pizzas, and each pizza is cut into 4 slices. You have 5 1/4 slices (5 whole pizzas plus 1 slice). Now you want to give away 2 3/4 slices (2 whole pizzas plus 3 slices). You can't directly give away 3 slices from just 1 slice. So, you take one of your whole pizzas and cut it into 4 slices. Now, you have 4 whole pizzas and 4 slices from the pizza you cut plus your initial slice. That's 4 5/4 slices. Now you can easily subtract 2 3/4 slices.
Alternative Method: Converting to Improper Fractions
Another approach involves converting both mixed numbers into improper fractions before subtracting. An improper fraction has a numerator larger than or equal to its denominator.
-
Convert 5 1/4 to an Improper Fraction: To do this, multiply the whole number (5) by the denominator (4), add the numerator (1), and keep the same denominator (4). This gives us (5 x 4) + 1 / 4 = 21/4.
-
Convert 2 3/4 to an Improper Fraction: Similarly, (2 x 4) + 3 / 4 = 11/4.
-
Subtract the Improper Fractions: Now subtract the improper fractions: 21/4 - 11/4 = 10/4.
-
Simplify and Convert Back to a Mixed Number: Simplify 10/4 by dividing both numerator and denominator by 2, resulting in 5/2. Then convert 5/2 back to a mixed number by dividing 5 by 2: 5 ÷ 2 = 2 with a remainder of 1. This gives us 2 1/2.
This method yields the same answer as the previous method, demonstrating the flexibility and equivalence of different approaches.
Common Mistakes to Avoid
-
Forgetting to Borrow: The most common mistake is failing to borrow when the fraction in the subtrahend is larger than the fraction in the minuend. This leads to an incorrect answer.
-
Incorrect Borrowing: Ensure you correctly convert the borrowed 1 into the equivalent fraction with the same denominator.
-
Errors in Fraction Simplification: Always simplify fractions to their lowest terms.
-
Incorrect Conversion to Improper Fractions: Double-check your calculations when converting between mixed numbers and improper fractions.
Frequently Asked Questions (FAQ)
-
Q: Can I subtract mixed numbers with different denominators? A: No, you must first find a common denominator for the fractions before subtracting.
-
Q: What if the result is a negative number? A: If, after subtracting the whole numbers, the fraction in the minuend is still smaller than the fraction in the subtrahend, you will end up with a negative mixed number or an improper fraction with a negative sign. For instance, 2 1/4 - 5 3/4 would result in a negative number.
-
Q: Are there other methods to solve mixed number subtraction problems? A: Yes, other methods exist, such as using a number line or visual representations, but the methods described above are the most efficient and commonly used.
-
Q: Why is borrowing necessary? A: Borrowing is essential because you cannot directly subtract a larger fraction from a smaller fraction. Borrowing allows us to redistribute the value of the whole number to the fraction part, enabling the subtraction.
-
Q: How can I practice mixed number subtraction? A: Practice regularly with various problems of increasing difficulty. You can find numerous online resources, worksheets, and textbooks that offer ample practice exercises.
Conclusion: Mastering Mixed Number Subtraction
Subtracting mixed numbers requires attention to detail and a methodical approach. By understanding the principles of borrowing, fraction simplification, and the alternative method of using improper fractions, you can confidently tackle any mixed number subtraction problem. Remember to check your work and practice regularly to solidify your understanding and improve your speed and accuracy. With consistent effort, you'll master this essential mathematical skill and gain a deeper understanding of fractions and mixed numbers. The solution to 5 1/4 - 2 3/4, as we've demonstrated, is 2 1/2, but the real takeaway is the confidence and understanding you gain in the process. This isn't just about solving one problem; it's about building a robust foundation for future mathematical challenges.
Latest Posts
Latest Posts
-
What Fractions Equal 2 3
Sep 18, 2025
-
30 Days From October 13
Sep 18, 2025
-
1 Out Of 7 Percentage
Sep 18, 2025
-
2 Divided By 3 Fraction
Sep 18, 2025
-
33 Acre To Sq Ft
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 1/4 - 2 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.