2 Divided By 3 Fraction
saludintensiva
Sep 18, 2025 · 6 min read
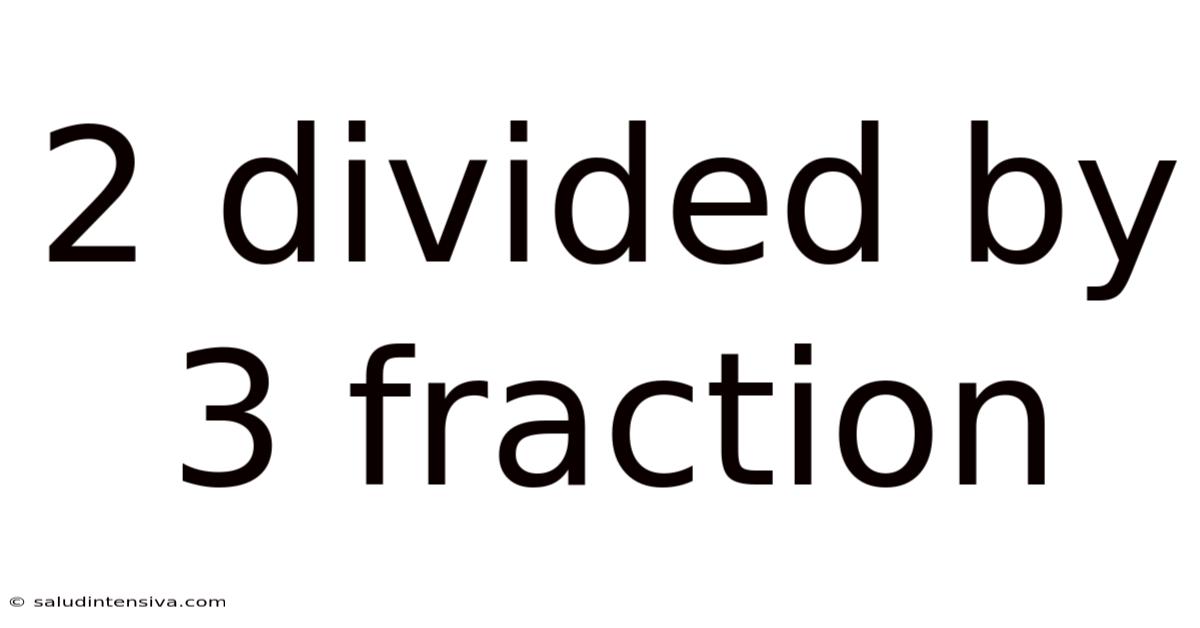
Table of Contents
Understanding 2 Divided by 3: A Deep Dive into Fractions and Division
Dividing fractions can seem daunting, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will explore the concept of 2 divided by 3, explaining it in a way that's accessible to everyone, from elementary school students to adults brushing up on their math skills. We'll cover various methods for solving this problem, explore the underlying mathematical concepts, and answer frequently asked questions. This comprehensive guide will leave you confident in your ability to tackle similar fraction division problems.
Understanding the Problem: 2 ÷ 3
The problem "2 divided by 3" asks: "How many times does 3 fit into 2?" Intuitively, we know that 3 is larger than 2, so 3 cannot fit into 2 a whole number of times. This means our answer will be a fraction, representing a part of a whole. This is where our understanding of fractions comes into play.
Method 1: Converting to a Fraction
The most straightforward method to solve 2 ÷ 3 is to express the division problem as a fraction. Any division problem can be written as a fraction where the dividend (the number being divided) is the numerator and the divisor (the number you're dividing by) is the denominator. Therefore, 2 ÷ 3 can be written as:
2/3
This fraction, two-thirds, is the simplest and most accurate representation of the answer. It means that if you divide 2 into 3 equal parts, each part will be 2/3.
Method 2: Using Long Division
While less efficient for this particular problem, long division can illustrate the process of dividing whole numbers that result in a fraction. Let's see how it works:
-
Set up the long division: Write 2 inside the long division symbol and 3 outside.
-
Perform the division: Since 3 cannot go into 2, we add a decimal point and a zero to the 2, making it 2.0. Now, 3 goes into 20 six times (3 x 6 = 18). Write 6 above the decimal point.
-
Subtract: Subtract 18 from 20, leaving a remainder of 2.
-
Continue the process: Add another zero to the remainder, making it 20. Again, 3 goes into 20 six times, resulting in a remainder of 2. This process will repeat infinitely.
-
Express as a decimal: The long division shows that 2 ÷ 3 is approximately 0.6666... This is a repeating decimal, often written as 0.6̅.
Method 3: Visual Representation
Visualizing the problem can enhance understanding. Imagine you have two pizzas. You want to divide these two pizzas equally among three people. How much pizza does each person get?
To solve this visually:
-
Divide each pizza: Cut each of the two pizzas into three equal slices.
-
Distribute the slices: You now have a total of six slices (2 pizzas x 3 slices/pizza).
-
Slices per person: Each person receives two of these six slices.
-
Fraction representation: Each person gets 2/6 of the pizza. This fraction can be simplified to 1/3 by dividing both the numerator and the denominator by 2. Note the discrepancy, which will be explained below.
The visual method highlights that the initial division creates six equal parts, leading to 2/6. However, the correct answer is 2/3 as our initial division was of two pizzas into 3 equal portions each. This clarifies why Method 1 is the most direct and efficient approach.
The Importance of Simplifying Fractions
In the visual representation, we obtained 2/6, which simplifies to 1/3. Simplifying fractions means reducing them to their lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). In this case, the GCD of 2 and 6 is 2.
Simplifying fractions doesn't change the value of the fraction; it just makes it easier to work with and understand. While 2/6 and 1/3 represent the same value, 1/3 is the simplified form and is generally preferred.
Understanding the Decimal Representation (0.6̅)
The repeating decimal 0.6̅ is another way to represent 2/3. This decimal goes on infinitely, with the digit 6 repeating. While decimals are useful in certain contexts, fractions often provide a more precise and concise representation, especially when dealing with calculations involving fractions.
Mathematical Explanation: The Reciprocal
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3 (or 3/1) is 1/3.
Therefore, 2 ÷ 3 is the same as 2 x (1/3) = 2/3. This demonstrates the mathematical equivalence between division and multiplication by the reciprocal.
Practical Applications of 2/3
The fraction 2/3 appears frequently in various contexts:
- Cooking: Many recipes use 2/3 cups of an ingredient.
- Measurement: Lengths or distances might be expressed as 2/3 of a meter or yard.
- Probability: The probability of an event could be 2/3.
- Data Analysis: Data sets might show that 2/3 of respondents agree on a certain issue.
Frequently Asked Questions (FAQ)
Q1: Can 2/3 be expressed as a percentage?
A1: Yes, to convert 2/3 to a percentage, divide the numerator by the denominator (2 ÷ 3 = 0.666...) and multiply by 100%. This gives approximately 66.67%.
Q2: How do I add or subtract fractions like 2/3?
A2: To add or subtract fractions, they need a common denominator. For example, to add 2/3 and 1/4, you'd find the least common multiple (LCM) of 3 and 4, which is 12. Then convert the fractions: (2/3) * (4/4) = 8/12 and (1/4) * (3/3) = 3/12. Adding them together gives 11/12.
Q3: How do I multiply fractions involving 2/3?
A3: Multiplying fractions is straightforward: multiply the numerators together and the denominators together. For example, (2/3) x (1/2) = (2 x 1) / (3 x 2) = 2/6 = 1/3.
Q4: How do I divide fractions involving 2/3?
A4: As mentioned earlier, dividing by a fraction is the same as multiplying by its reciprocal. For example, (2/3) ÷ (1/2) = (2/3) x (2/1) = 4/3.
Conclusion
Dividing 2 by 3 results in the fraction 2/3, representing two parts out of three equal parts. While it can be expressed as a repeating decimal (0.6̅), the fraction form is often more precise and easier to use in further calculations. Understanding the different methods to solve this problem—converting to a fraction, using long division, and visual representation—provides a solid foundation for tackling more complex fraction division problems. Remember the importance of simplifying fractions to their lowest terms for clarity and ease of use. This comprehensive guide should equip you with the knowledge and confidence to confidently handle fraction division in any context.
Latest Posts
Latest Posts
-
0 48 Acres To Sq Ft
Sep 18, 2025
-
3 5 Is Equivalent To
Sep 18, 2025
-
1 24 As A Percentage
Sep 18, 2025
-
Time Zone Converter Excel Formula
Sep 18, 2025
-
29 6 As A Decimal
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 Divided By 3 Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.