4 16 As A Percent
saludintensiva
Sep 14, 2025 · 5 min read
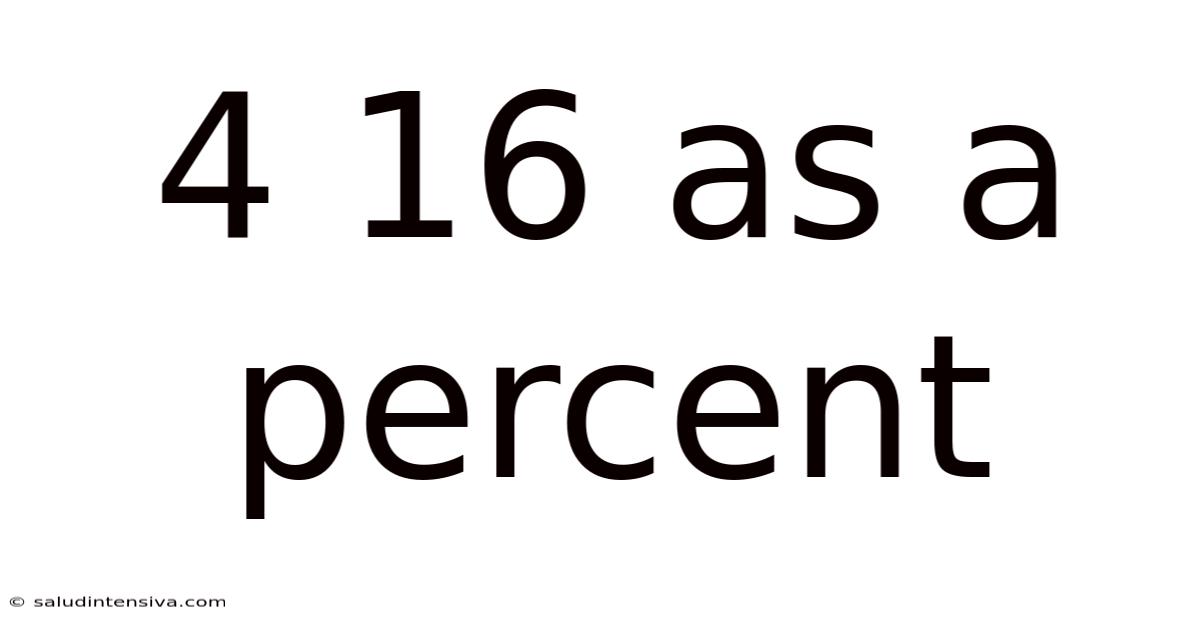
Table of Contents
Understanding 4/16 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 4/16 into a percentage, exploring the underlying concepts and providing a detailed, step-by-step approach. We'll also address common misconceptions and answer frequently asked questions. This will not only show you how to calculate 4/16 as a percent but also equip you with a broader understanding of percentage calculations.
Understanding Fractions and Percentages
Before we tackle the conversion of 4/16 to a percentage, let's clarify the basic concepts. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). In the fraction 4/16, 4 is the numerator and 16 is the denominator. This means we have 4 parts out of a total of 16 parts.
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," which means "out of one hundred." For example, 50% means 50 out of 100, which can also be written as the fraction 50/100 or the decimal 0.5.
Simplifying the Fraction 4/16
The first step in converting 4/16 to a percentage is to simplify the fraction. Simplifying a fraction means reducing it to its lowest terms. We do this by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it.
The GCD of 4 and 16 is 4. Dividing both the numerator and the denominator by 4, we get:
4 ÷ 4 = 1 16 ÷ 4 = 4
Therefore, the simplified fraction is 1/4. This means that 4/16 and 1/4 represent the same value. Working with the simplified fraction makes the conversion to a percentage much easier.
Converting the Simplified Fraction to a Percentage
Now that we have the simplified fraction 1/4, we can convert it to a percentage. There are two main methods to achieve this:
Method 1: Using the Division Method
This method involves dividing the numerator by the denominator and then multiplying the result by 100.
1 ÷ 4 = 0.25
0.25 x 100 = 25%
Therefore, 1/4 (and consequently, 4/16) is equal to 25%.
Method 2: Using the Proportion Method
This method involves setting up a proportion to find the equivalent percentage. We know that a percentage is a fraction out of 100. So we can set up the following proportion:
1/4 = x/100
To solve for x (the percentage), we cross-multiply:
4x = 100
x = 100 ÷ 4
x = 25
Therefore, 1/4 (and consequently, 4/16) is equal to 25%.
Visual Representation: Understanding 25%
It's helpful to visualize what 25% represents. Imagine a pizza cut into four equal slices. Each slice represents 1/4 or 25% of the whole pizza. Taking one slice means you have 25% of the pizza. This visual representation makes the concept of percentages more intuitive.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in various real-world scenarios:
- Calculating Discounts: If a store offers a 25% discount on an item, you can use this knowledge to quickly calculate the final price.
- Analyzing Data: In statistics and data analysis, percentages are often used to represent proportions and trends.
- Financial Calculations: Percentages are essential for calculating interest rates, taxes, and profits.
- Everyday Life: We encounter percentages in various situations, from calculating tips to understanding nutritional information on food labels.
Common Misconceptions about Percentage Calculations
- Confusing Fractions with Percentages: While closely related, fractions and percentages are not interchangeable. A fraction represents a part of a whole, while a percentage represents that part as a fraction of 100.
- Incorrectly Simplifying Fractions: Failing to simplify a fraction before converting it to a percentage can lead to inaccurate results. Always simplify the fraction to its lowest terms.
- Forgetting to Multiply by 100: When converting a decimal to a percentage, remember to multiply the decimal by 100 and add the percentage sign.
Frequently Asked Questions (FAQs)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage using the methods described above.
Q: What if the fraction results in a repeating decimal?
A: If the division results in a repeating decimal, you can round the decimal to a certain number of decimal places before multiplying by 100. For example, 1/3 = 0.333... Rounding to two decimal places gives 0.33, and multiplying by 100 gives 33%.
Q: Is there a shortcut to convert fractions with a denominator of 100?
A: Yes, if the denominator is already 100, the numerator directly represents the percentage. For example, 75/100 = 75%.
Q: What about fractions greater than 1?
A: Fractions greater than 1 (improper fractions) will result in percentages greater than 100%. For example, 5/2 = 2.5, and 2.5 * 100 = 250%. This indicates that the numerator is 250% of the denominator.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with wide-ranging applications. By understanding the underlying principles and applying the methods outlined in this guide, you can confidently convert any fraction to a percentage. Remember to simplify the fraction first and to multiply the decimal result by 100 to obtain the percentage. The process is straightforward, and mastering it will greatly enhance your mathematical abilities and problem-solving skills in various contexts. The conversion of 4/16 to 25% serves as a practical example of this valuable skill, showcasing its simplicity and relevance. Through consistent practice and a clear understanding of the concepts, you can confidently tackle similar percentage calculations in your academic pursuits and daily life. Remember, the key is to break down the problem into manageable steps and to understand the reasoning behind each step.
Latest Posts
Latest Posts
-
14 20 As A Percent
Sep 14, 2025
-
What Is 80 Of 5
Sep 14, 2025
-
What Percent Is 15 20
Sep 14, 2025
-
What Percentage Is 1 4
Sep 14, 2025
-
3 To The 6th Power
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4 16 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.