4 30 As A Percent
saludintensiva
Sep 24, 2025 · 5 min read
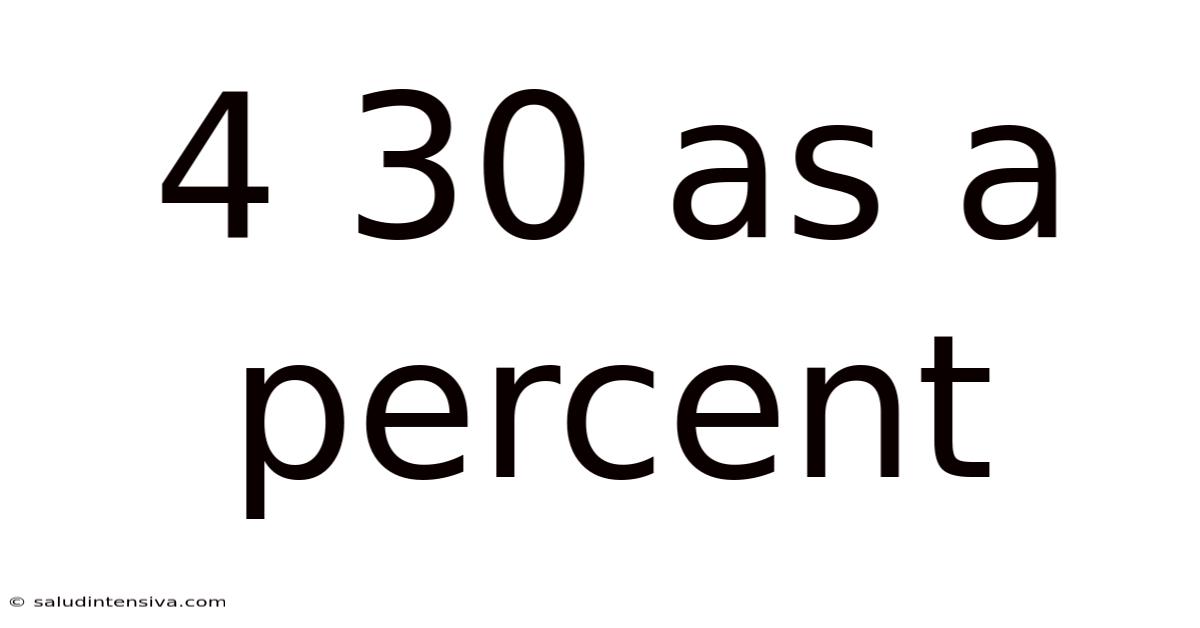
Table of Contents
4/30 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts and tips to comprehending statistical data and analyzing financial reports. This article provides a comprehensive guide on how to convert the fraction 4/30 into a percentage, explaining the process step-by-step and delving into the underlying mathematical concepts. We'll also explore various methods and address common questions, ensuring a thorough understanding for learners of all levels. This guide covers everything from the basic arithmetic to the practical implications of understanding percentage calculations.
Introduction: Understanding Fractions and Percentages
Before diving into the specific conversion of 4/30, let's establish a clear understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 4/30, 4 is the numerator and 30 is the denominator, indicating 4 parts out of a total of 30 parts.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. Understanding this fundamental relationship between fractions and percentages is key to performing conversions.
Method 1: Simplifying the Fraction before Conversion
The first step in converting 4/30 to a percentage involves simplifying the fraction. Simplifying a fraction means reducing it to its lowest terms by finding the greatest common divisor (GCD) of the numerator and the denominator. In this case, the GCD of 4 and 30 is 2. Dividing both the numerator and denominator by 2, we get:
4 ÷ 2 = 2 30 ÷ 2 = 15
Therefore, 4/30 simplifies to 2/15. This simplified fraction is equivalent to the original fraction but is easier to work with for the next steps.
Method 2: Converting the Simplified Fraction to a Decimal
To convert the simplified fraction 2/15 to a percentage, we first need to convert it into a decimal. This is done by dividing the numerator by the denominator:
2 ÷ 15 ≈ 0.1333...
The result is a repeating decimal, approximately 0.1333. Note that the "…" indicates that the digit 3 repeats infinitely.
Method 3: Converting the Decimal to a Percentage
Finally, to convert the decimal 0.1333... to a percentage, we multiply it by 100 and add the percent sign (%):
0.1333... × 100 ≈ 13.33%
Therefore, 4/30 is approximately equal to 13.33%. The use of the approximation symbol (≈) acknowledges the repeating decimal nature of the result. In practical applications, rounding to two decimal places (13.33%) is usually sufficient.
Alternative Method: Direct Conversion
While the above method is generally preferred for clarity and understanding, it's also possible to convert the fraction directly to a percentage without simplifying:
- Divide the numerator (4) by the denominator (30): 4 ÷ 30 ≈ 0.1333...
- Multiply the result by 100: 0.1333... × 100 ≈ 13.33%
This method yields the same result but skips the simplification step.
Understanding the Mathematical Principles
The conversion from a fraction to a percentage fundamentally relies on the concept of proportions. A fraction represents a ratio, and a percentage is a specific type of ratio – a ratio out of 100. The process of conversion involves finding the equivalent ratio that has a denominator of 100. This is achieved through the steps of simplification (if possible) and decimal-to-percentage conversion.
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages has numerous practical applications in various fields:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Statistics: Representing data proportions, analyzing survey results, and interpreting probabilities.
- Retail: Determining sale prices, calculating markups, and understanding discounts.
- Science: Expressing experimental results, calculating concentrations, and representing data in graphical form.
- Everyday life: Calculating tips, splitting bills, and understanding proportions in recipes.
Frequently Asked Questions (FAQ)
Q: Is 13.33% the exact value or an approximation?
A: 13.33% is an approximation. The decimal representation of 2/15 (or 4/30) is a repeating decimal (0.1333...), meaning the digit 3 repeats infinitely. Rounding to two decimal places is a common practice for practical applications, but the exact value is a non-terminating decimal.
Q: Why is simplifying the fraction helpful?
A: Simplifying the fraction makes the subsequent division easier and reduces the chance of errors in calculation. It allows for working with smaller numbers, facilitating a more straightforward conversion.
Q: Can I convert any fraction to a percentage using this method?
A: Yes, this method can be applied to convert any fraction to a percentage. The steps remain the same: simplify (if possible), convert to a decimal by dividing the numerator by the denominator, and then multiply the decimal by 100 to get the percentage.
Q: What if the decimal conversion results in a terminating decimal (not a repeating one)?
A: If the decimal conversion results in a terminating decimal, the multiplication by 100 will yield a precise percentage without any need for rounding.
Q: What are some common mistakes to avoid when converting fractions to percentages?
A: Common mistakes include: incorrectly simplifying the fraction, making errors in the division process, forgetting to multiply the decimal by 100, and not understanding the difference between an exact and approximate value.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with broad applications in diverse fields. By understanding the underlying principles and following the step-by-step process outlined in this article, one can confidently convert any fraction to its percentage equivalent. Mastering this skill not only enhances mathematical proficiency but also equips individuals with practical tools for navigating various real-world scenarios that involve proportional reasoning and quantitative analysis. Remember that accuracy and attention to detail are key throughout the conversion process, ensuring reliable and meaningful results. Practice is essential to build confidence and fluency in these crucial mathematical operations.
Latest Posts
Latest Posts
-
What Does Percentile Rank Mean
Sep 24, 2025
-
Use Excel To Calculate Age
Sep 24, 2025
-
Unit For Coefficient Of Friction
Sep 24, 2025
-
Find Equation Of Parallel Line
Sep 24, 2025
-
How To Pronounce Large Numbers
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 30 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.