4 5 Is Equivalent To
saludintensiva
Sep 13, 2025 · 5 min read
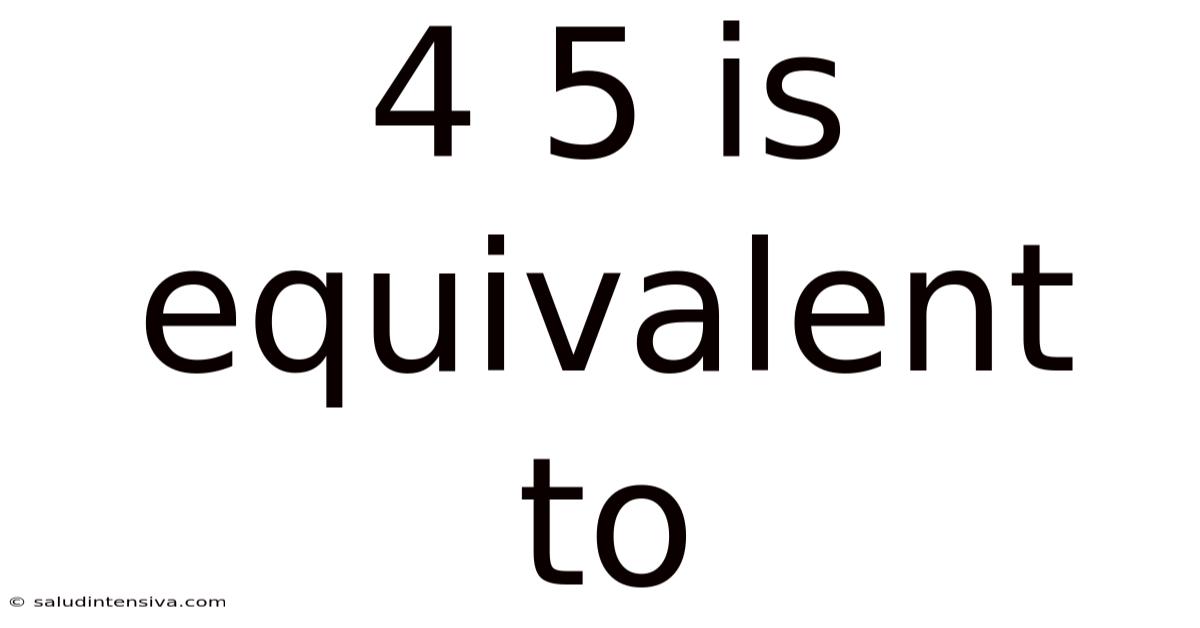
Table of Contents
4/5 is Equivalent To: Exploring Fractions, Decimals, Percentages, and Ratios
Understanding the equivalence of fractions, decimals, percentages, and ratios is fundamental to grasping mathematical concepts across various disciplines. This article delves into the multifaceted nature of the fraction 4/5, demonstrating its equivalence across different mathematical representations. We'll explore how 4/5 translates into decimals, percentages, and ratios, providing practical examples and explanations to solidify your understanding. This comprehensive guide will equip you with the skills to confidently work with equivalent forms of fractions in any context.
Understanding Fractions: The Foundation of Equivalence
Before we explore the equivalence of 4/5, let's establish a firm understanding of fractions themselves. A fraction represents a part of a whole. It is expressed as a numerator (the top number) divided by a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In the fraction 4/5, 4 is the numerator and 5 is the denominator. This means we have 4 parts out of a possible 5 equal parts.
Key Properties of Fractions:
-
Equivalent Fractions: Different fractions can represent the same value. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. This occurs because multiplying or dividing both the numerator and the denominator by the same non-zero number doesn't change the fraction's value.
-
Simplifying Fractions: To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. This reduces the fraction to its simplest form. For example, 6/9 can be simplified to 2/3 by dividing both the numerator and the denominator by 3 (the GCD of 6 and 9).
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to its denominator (e.g., 7/4). A mixed number combines a whole number and a proper fraction (e.g., 1 ¾). Improper fractions can be converted into mixed numbers and vice versa.
4/5 as a Decimal: The Process of Conversion
Converting a fraction to a decimal involves dividing the numerator by the denominator. In the case of 4/5:
4 ÷ 5 = 0.8
Therefore, 4/5 is equivalent to 0.8. This decimal representation signifies eight-tenths.
4/5 as a Percentage: From Fraction to Percentage
A percentage expresses a fraction as a portion of 100. To convert a fraction to a percentage, we first convert it to a decimal and then multiply by 100%. Let's illustrate this with 4/5:
- Convert the fraction to a decimal: 4/5 = 0.8
- Multiply the decimal by 100%: 0.8 x 100% = 80%
Therefore, 4/5 is equivalent to 80%. This indicates that 4/5 represents 80 parts out of 100.
4/5 as a Ratio: Expressing Relationships
A ratio compares two or more quantities. While 4/5 is already expressed as a ratio (4 to 5), we can represent it in different ways. For example:
-
4:5: This is the simplest and most common way to express the ratio of 4 to 5. It signifies that for every 4 units of one quantity, there are 5 units of another.
-
4/5: The fraction itself represents the ratio.
-
Other equivalent ratios: Just as with fractions, ratios can have equivalent forms. Multiplying or dividing both parts of the ratio by the same number yields an equivalent ratio. For example, 8:10, 12:15, and 20:25 are all equivalent to 4:5.
Real-World Applications of 4/5 Equivalence
The equivalence of 4/5 finds practical applications in numerous real-world scenarios:
-
Discounts: An 80% discount is equivalent to a 4/5 reduction in price.
-
Surveys: If 80 out of 100 people surveyed prefer a particular product, this represents a 4/5 preference.
-
Measurements: If a recipe calls for 4 out of 5 cups of flour, it can be represented as 0.8 cups or 80% of a cup.
-
Progress: Completing 4 out of 5 tasks represents 80% of the project's completion.
Deeper Dive: Understanding the Mathematical Principles
The ability to convert between fractions, decimals, percentages, and ratios relies on fundamental mathematical principles:
-
Division: Converting a fraction to a decimal involves performing division.
-
Proportionality: Equivalent fractions and ratios maintain proportionality – a constant relationship between their parts.
-
Percentage as a Fraction: Percentages are essentially fractions with a denominator of 100.
-
Ratio as a Comparison: Ratios compare quantities and can be expressed in various forms, including fractions.
Frequently Asked Questions (FAQ)
Q1: Can I simplify 4/5 further?
A1: No. 4 and 5 have no common divisors other than 1. Therefore, 4/5 is already in its simplest form.
Q2: What if I have a more complex fraction, like 12/15? How do I find its equivalent forms?
A2: Simplify the fraction first by finding the GCD of the numerator and denominator (in this case, 3). Dividing both by 3 gives you 4/5. Then, you can use the methods described above to find its decimal, percentage, and ratio equivalents.
Q3: Are all ratios expressed as fractions?
A3: While ratios can be represented as fractions, they can also be expressed using colons (e.g., 4:5) or in words (e.g., "the ratio of 4 to 5").
Q4: How do I convert a decimal to a fraction?
A4: For a decimal like 0.8, you can write it as 8/10 and then simplify it by dividing both the numerator and denominator by their GCD (2), resulting in 4/5.
Conclusion: Mastering Equivalence for Mathematical Fluency
Understanding the equivalence of 4/5, and fractions in general, is crucial for mathematical fluency. The ability to seamlessly convert between fractions, decimals, percentages, and ratios expands your mathematical toolkit and allows you to approach problems from different perspectives. This comprehensive guide has provided you with the necessary tools and understanding to confidently work with equivalent forms of fractions, empowering you to tackle a wider range of mathematical challenges. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. By mastering these concepts, you'll not only improve your mathematical skills but also enhance your problem-solving capabilities across various fields.
Latest Posts
Latest Posts
-
Least To Greatest Calculator Decimals
Sep 13, 2025
-
19 50 As A Decimal
Sep 13, 2025
-
2 7 As A Decimal
Sep 13, 2025
-
What Is 2 2 Simplified
Sep 13, 2025
-
Lowest Term Of 5 20
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 4 5 Is Equivalent To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.