4 5 X 1 6
saludintensiva
Sep 16, 2025 · 6 min read
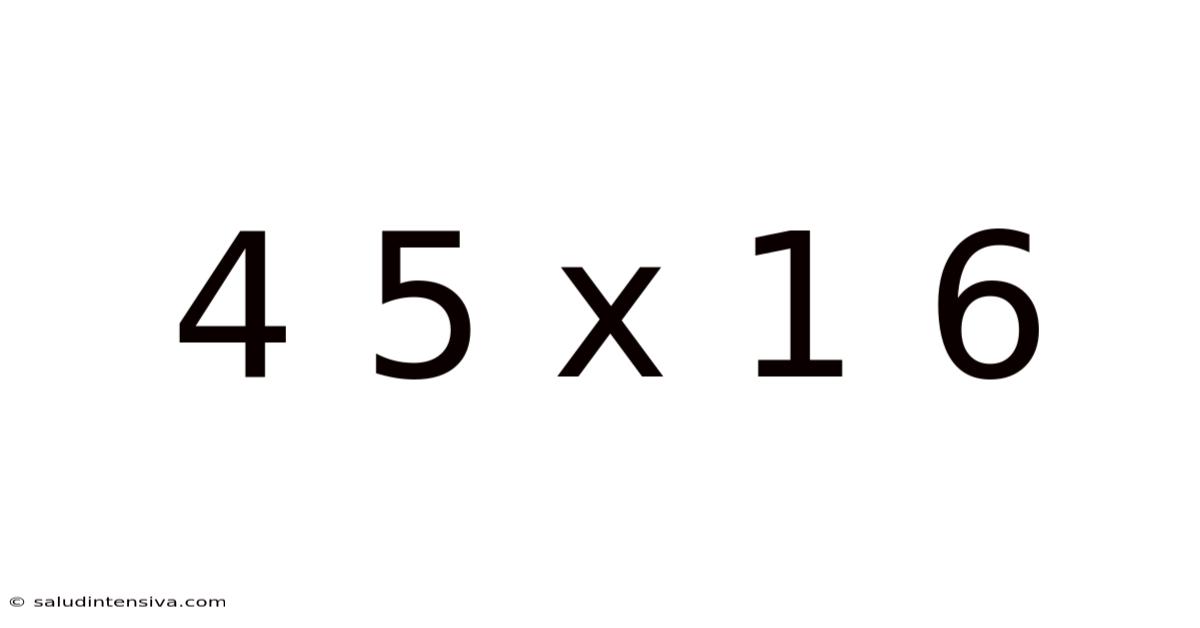
Table of Contents
Decoding 45 x 16: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 45 x 16, and expands upon it to delve into the fundamental principles of multiplication, different methods for solving it, and its relevance in various fields. Understanding this seemingly basic calculation unlocks a broader comprehension of mathematics and its practical applications in everyday life and beyond. We'll cover everything from the basic arithmetic to advanced concepts related to this calculation, making it accessible for learners of all levels.
Introduction: The Foundation of Multiplication
Multiplication, at its core, is repeated addition. When we say 45 x 16, we're essentially adding 45 sixteen times: 45 + 45 + 45 + ... + 45 (sixteen times). This fundamental understanding is crucial, particularly for beginners. While calculators provide instant answers, grasping the underlying principles is essential for developing a strong mathematical foundation. This article will not only show you how to solve 45 x 16, but also why the methods work, empowering you with a deeper understanding of the process.
Methods for Solving 45 x 16
Several approaches can be used to solve 45 x 16. Let's explore the most common and effective methods:
1. Standard Multiplication Algorithm
This is the traditional method taught in schools. It involves multiplying each digit of one number by each digit of the other, then adding the partial products.
-
Step 1: Multiply 45 by 6 (the ones digit of 16): 5 x 6 = 30 (write down 0, carry-over 3) 4 x 6 = 24 + 3 (carry-over) = 27 (write down 270)
-
Step 2: Multiply 45 by 10 (the tens digit of 16): 5 x 10 = 50 (write down 0, carry-over 5) 4 x 10 = 40 + 5 (carry-over) = 45 (write down 450)
-
Step 3: Add the partial products: 270 + 450 = 720
Therefore, 45 x 16 = 720.
2. Distributive Property
The distributive property states that a(b + c) = ab + ac. We can use this to break down the problem:
45 x 16 = 45 x (10 + 6) = (45 x 10) + (45 x 6) = 450 + 270 = 720
3. Lattice Multiplication
This method, less commonly used but visually appealing, involves a grid.
- Create a grid with two rows (for the digits of 45) and two columns (for the digits of 16).
- Multiply each digit combination (4x1, 4x6, 5x1, 5x6) and write the result in the corresponding cell, splitting tens and ones diagonally.
- Add the diagonals, starting from the bottom right. This gives you the final answer: 720. (Diagram would be visually helpful here but cannot be created in this text format).
4. Using Mental Math Techniques
With practice, you can solve this mentally. For example:
- Breaking it down: 45 x 16 can be thought of as (45 x 10) + (45 x 6) = 450 + 270 = 720
- Doubling and Halving: 16 is double 8, so we can calculate 45 x 8 (360) and double the result (720).
Applications of Multiplication: Beyond the Classroom
The seemingly simple operation of 45 x 16 has broad applications across various disciplines:
-
Everyday Calculations: From calculating the total cost of 16 items at $45 each to figuring out the area of a rectangular space (45 units by 16 units), multiplication is an integral part of daily life.
-
Business and Finance: Calculating profits, losses, taxes, and investments heavily rely on multiplication. For example, calculating the total revenue from selling 16 units of a product priced at $45 each.
-
Engineering and Construction: Engineers and architects use multiplication extensively in design calculations, from structural load calculations to determining material quantities.
-
Science: Scientific research often involves analyzing data that requires extensive multiplication. This is crucial in various fields like physics, chemistry, and biology.
-
Computer Science: Multiplication is a fundamental operation in computer programming and algorithm design.
Expanding on the Concept: Factors and Multiples
Understanding the concept of factors and multiples is essential when working with multiplication.
-
Factors: Factors are numbers that divide evenly into another number without leaving a remainder. The factors of 720 (the result of 45 x 16) include 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360, and 720.
-
Multiples: Multiples are numbers that are the product of a given number and any other integer. The multiples of 45 include 45, 90, 135, 180, 225, 270, 315, 360, 405, 450, 495, 540, 585, 630, 675, 720... Similarly, the multiples of 16 include 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288, 304, 320, 336, 352, 368, 384, 400, 416, 432, 448, 464, 480, 496, 512, 528, 544, 560, 576, 592, 608, 624, 640, 656, 672, 688, 704, and 720.
Prime Factorization and the Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (numbers divisible only by 1 and themselves). Let's find the prime factorization of 720:
720 = 2 x 360 = 2 x 2 x 180 = 2 x 2 x 2 x 90 = 2 x 2 x 2 x 2 x 45 = 2 x 2 x 2 x 2 x 3 x 15 = 2 x 2 x 2 x 2 x 3 x 3 x 5 = 2⁴ x 3² x 5
This prime factorization is unique to 720 and provides valuable insights into its properties.
Exploring Advanced Concepts: Modular Arithmetic and Number Theory
While beyond the scope of a basic multiplication problem, 45 x 16 can serve as a starting point for exploring more advanced mathematical concepts. For example, modular arithmetic examines the remainders when numbers are divided by a specific modulus. Number theory delves into the properties of numbers, including prime numbers, divisibility, and congruences. Understanding 45 x 16 lays a foundation for comprehending these more sophisticated mathematical realms.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to solve 45 x 16? A: The easiest method depends on your individual preferences and mathematical skills. The standard algorithm, distributive property, or mental math techniques can all be effective.
-
Q: Are there any tricks to make multiplication faster? A: Yes, practicing mental math techniques, understanding the distributive property, and learning different multiplication methods can significantly increase your speed and accuracy.
-
Q: Why is it important to learn multiplication? A: Multiplication is a fundamental mathematical operation with applications across numerous fields, enabling us to solve real-world problems efficiently.
Conclusion: Mastering the Fundamentals
The seemingly simple calculation of 45 x 16 opens a door to a vast world of mathematical understanding. By exploring different methods, grasping the underlying principles, and understanding its applications, we appreciate the power and relevance of even the most basic mathematical operations. From everyday calculations to complex scientific analyses, a firm grasp of multiplication forms the cornerstone of numerical literacy and problem-solving abilities. Continue practicing, explore different methods, and remember that a deep understanding of the fundamentals is key to unlocking more advanced mathematical concepts. The journey of mathematical learning is continuous, and mastering the basics like 45 x 16 is the first crucial step.
Latest Posts
Latest Posts
-
14 Percent As A Decimal
Sep 16, 2025
-
Two Equivalent Fractions Of 3 4
Sep 16, 2025
-
What Is Half Of 47
Sep 16, 2025
-
What Percentage Is 2 5
Sep 16, 2025
-
2 To The 11 Power
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 4 5 X 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.