4 6 As A Percent
saludintensiva
Sep 03, 2025 · 5 min read
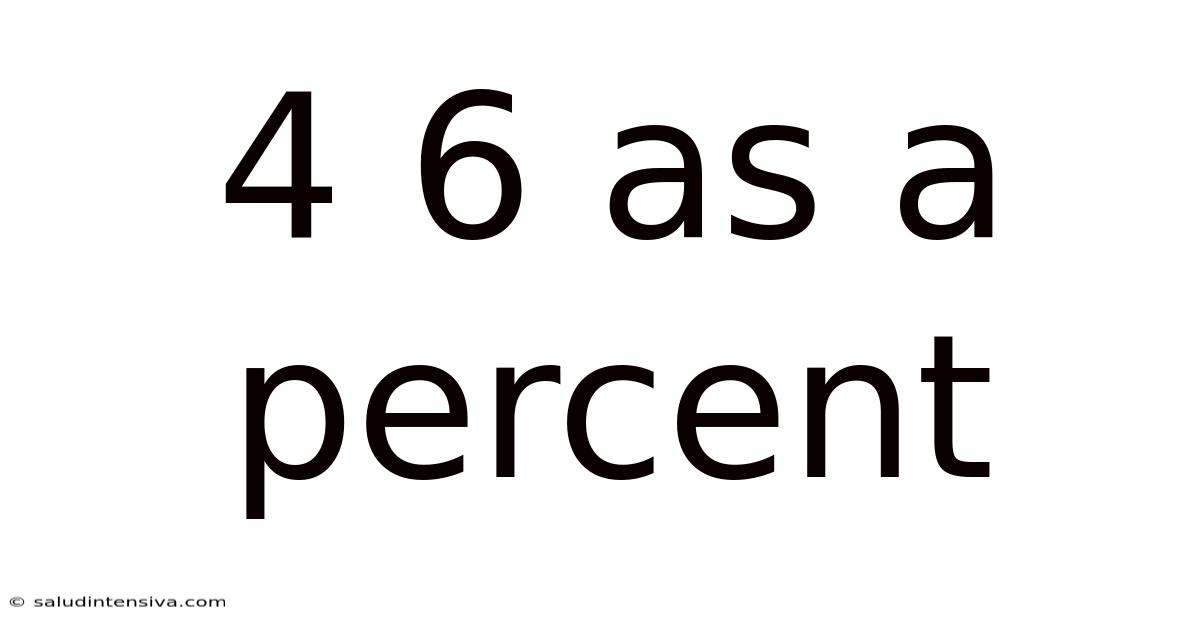
Table of Contents
Understanding 4/6 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts to understanding statistical data. This comprehensive guide will delve into how to convert the fraction 4/6 into a percentage, exploring various methods and providing a deeper understanding of the underlying concepts. We'll cover multiple approaches, addressing potential difficulties and offering practical examples to solidify your grasp of this crucial mathematical concept.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before we dive into converting 4/6 to a percentage, let's refresh our understanding of the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
- A fraction expresses a part of a whole as a ratio of two numbers (numerator/denominator). For example, 4/6 means 4 parts out of a total of 6 parts.
- A decimal represents a fraction using base-10 notation, with a decimal point separating the whole number part from the fractional part.
- A percentage expresses a fraction or decimal as a proportion of 100, denoted by the symbol %.
These three forms are interchangeable, meaning you can convert one into another without changing the underlying value. Understanding this interconnectedness is crucial for solving various mathematical problems.
Method 1: Simplifying the Fraction
The first step in converting 4/6 to a percentage is often to simplify the fraction. Simplifying means reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 4 and 6 is 2. Dividing both the numerator and the denominator by 2, we get:
4/6 = (4 ÷ 2) / (6 ÷ 2) = 2/3
Simplifying the fraction makes the subsequent conversion to a percentage easier and often provides a clearer understanding of the proportion.
Method 2: Converting the Simplified Fraction to a Decimal
Now that we have the simplified fraction 2/3, we can convert it to a decimal by performing the division:
2 ÷ 3 ≈ 0.666666...
Notice that this decimal is a repeating decimal, meaning the digit 6 repeats infinitely. For practical purposes, we often round the decimal to a certain number of decimal places. For example, rounding to two decimal places, we get 0.67.
Method 3: Converting the Decimal to a Percentage
To convert the decimal 0.666666... (or its rounded version 0.67) to a percentage, we multiply it by 100 and add the % symbol:
0.666666... × 100 ≈ 66.6666...%
Rounding to two decimal places, we get approximately 66.67%. Therefore, 4/6 is approximately 66.67%. Remember that this is an approximation due to the rounding of the repeating decimal.
Method 4: Direct Percentage Calculation from the Fraction
Alternatively, we can calculate the percentage directly from the original fraction 4/6 without simplifying. To do this, we set up a proportion:
4/6 = x/100
Where 'x' represents the percentage we're trying to find. We can solve for 'x' by cross-multiplying:
6x = 400
x = 400/6
x ≈ 66.67
Again, this gives us approximately 66.67%.
Understanding the Concept of Percentages
Percentages are fundamentally about expressing proportions relative to 100. When we say something is 66.67%, we're saying it's 66.67 parts out of 100. This standardized representation makes it easier to compare different proportions and understand them intuitively. Imagine a pie chart representing a whole; 66.67% would occupy a significant portion of that chart.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is widely used in various real-world scenarios. Consider these examples:
- Sales and Discounts: If a store offers a 25% discount on an item, you can easily calculate the discount amount and the final price.
- Financial Calculations: Interest rates, tax calculations, and investment returns are all expressed as percentages.
- Statistical Analysis: Percentages are frequently used to represent data in charts and graphs, making it easy to visualize and interpret information.
- Everyday Life: From calculating tips in restaurants to understanding nutritional information on food labels, percentages play a vital role in our daily lives.
Addressing Potential Difficulties and Common Mistakes
One common mistake is forgetting to multiply the decimal by 100 when converting to a percentage. Remember, a percentage is always a fraction of 100.
Another difficulty arises with repeating decimals. While mathematically precise, they can be cumbersome to work with in practice. Rounding to a reasonable number of decimal places is often necessary for practical applications. However, it's important to be aware that this introduces a small degree of approximation.
Frequently Asked Questions (FAQ)
-
Q: Is there a difference between 66.67% and 66.666...? A: Yes, there's a small difference. 66.67% is a rounded approximation of the repeating decimal 66.666...%. The exact value is represented by the repeating decimal.
-
Q: Why is simplifying the fraction helpful? A: Simplifying reduces the complexity of the numbers, making both the division and subsequent calculations easier and potentially reducing errors.
-
Q: Can I use a calculator for these conversions? A: Yes, calculators can greatly simplify the process of converting fractions to decimals and percentages. Many calculators have built-in functions for these conversions.
-
Q: What if the fraction is larger than 1 (e.g., 7/3)? A: For fractions greater than 1, you would follow the same process: convert to a decimal (in this case, 2.333...), then multiply by 100 to find the percentage (233.33%).
Conclusion: Mastering Percentage Conversions
The ability to convert fractions to percentages is a fundamental skill with far-reaching applications. By understanding the different methods and the underlying concepts, you can confidently tackle various problems involving percentages in your academic pursuits, professional life, and everyday situations. Remember the key steps: simplify the fraction (if possible), convert to a decimal using division, and then multiply by 100 to obtain the percentage. Practice makes perfect; with consistent effort, you'll master this crucial mathematical skill and unlock a deeper understanding of how proportions are represented and used. From calculating discounts to understanding statistical data, the ability to seamlessly work with percentages will prove invaluable. Remember to always double-check your work and consider the context to determine the appropriate level of precision for your answer.
Latest Posts
Latest Posts
-
Adding Positive And Negative Fractions
Sep 08, 2025
-
0 34 Acres To Square Feet
Sep 08, 2025
-
43 C Is What Fahrenheit
Sep 08, 2025
-
Long Division Problems With Remainders
Sep 08, 2025
-
16 To The Power Of
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 4 6 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.