4 Divided By 2 3
saludintensiva
Sep 23, 2025 · 5 min read
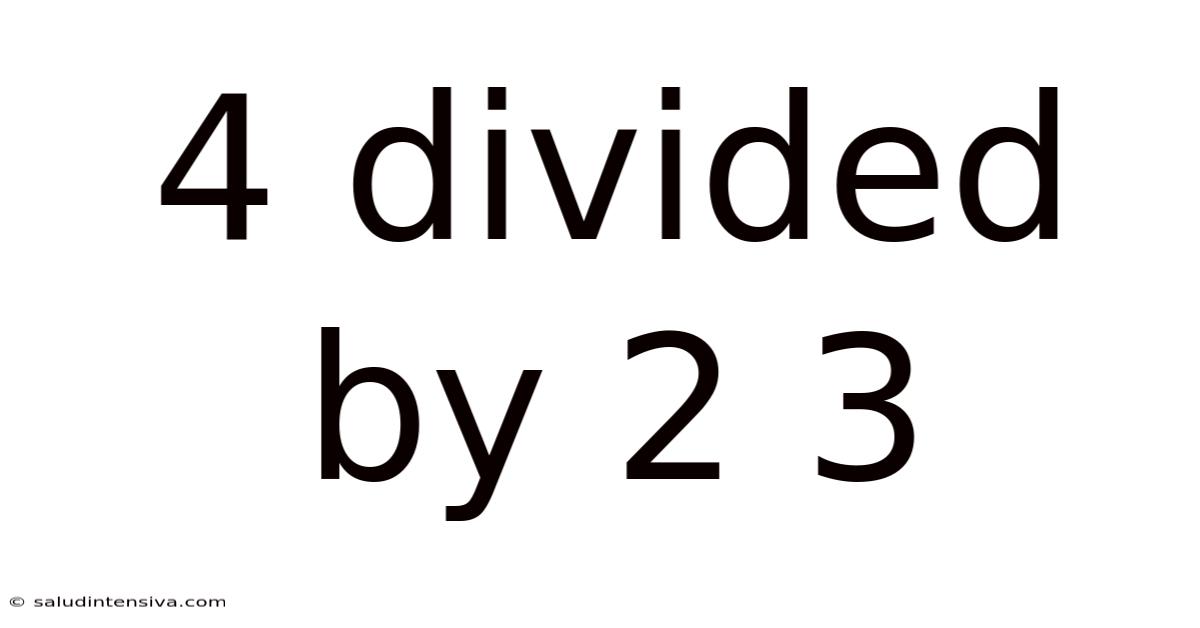
Table of Contents
Decoding 4 Divided by 2/3: A Deep Dive into Fraction Division
The seemingly simple question, "What is 4 divided by 2/3?", often trips up students and even adults. This isn't because the math is inherently difficult, but because the concept of dividing by a fraction requires a solid understanding of fractions themselves and the principles of division. This article will break down this calculation step-by-step, explore the underlying mathematical principles, and answer frequently asked questions to ensure a complete understanding. We'll move beyond simply providing the answer and delve into the why behind the solution.
Understanding the Problem: 4 ÷ (2/3)
Before we begin the calculation, let's clarify the problem. We're asked to divide the whole number 4 by the fraction 2/3. This means we're essentially asking: "How many times does 2/3 fit into 4?" This framing can make the problem more intuitive. Imagine you have 4 pizzas, and you want to know how many servings of 2/3 of a pizza you can make.
Step-by-Step Calculation: The "Keep, Change, Flip" Method
The most common method for dividing fractions is the "keep, change, flip" method (also known as the reciprocal method). This method simplifies the process significantly. Here's how it works for our problem:
-
Keep: Keep the first number (the dividend) exactly as it is. In our case, this remains 4. We can rewrite 4 as a fraction: 4/1.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip the second number (the divisor) – this means finding its reciprocal. The reciprocal of 2/3 is 3/2.
So our problem now looks like this:
(4/1) × (3/2)
- Multiply: Now, we simply multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(4 × 3) / (1 × 2) = 12/2
- Simplify: Finally, we simplify the resulting fraction. 12 divided by 2 is 6.
Therefore, 4 divided by 2/3 equals 6.
Visualizing the Solution
To further solidify your understanding, let's visualize this with a simple diagram. Imagine four identical bars representing the number 4. Now, we need to divide these bars into segments of 2/3 each.
[Imagine a diagram here with four bars, each divided into three sections. Two of the sections in each bar are shaded, indicating 2/3. There should be a total of six shaded segments across all four bars.]
Each bar can be divided into 1 and 1/3 portions of 2/3. Since we have 4 bars, we have 6 portions of 2/3 in total. This visualization confirms our calculated answer of 6.
The Mathematical Rationale Behind "Keep, Change, Flip"
Why does the "keep, change, flip" method work? It's rooted in the definition of division. Dividing by a fraction is the same as multiplying by its reciprocal. This is because division is the inverse operation of multiplication.
Think about dividing by 2. It's the same as multiplying by 1/2. Similarly, dividing by 2/3 is the same as multiplying by 3/2. The "keep, change, flip" method is simply a shortcut that encapsulates this mathematical principle.
Dealing with Mixed Numbers
What if the problem involved a mixed number? For instance, what if we were asked to calculate 2 1/2 divided by 2/3?
First, we convert the mixed number into an improper fraction. 2 1/2 is the same as (2 × 2 + 1)/2 = 5/2. Then, we apply the "keep, change, flip" method:
(5/2) ÷ (2/3) becomes (5/2) × (3/2) = 15/4
This improper fraction can be converted back into a mixed number: 3 3/4.
Therefore, 2 1/2 divided by 2/3 equals 3 3/4.
Beyond the Calculation: Real-World Applications
Understanding fraction division isn't just about solving textbook problems. It has numerous practical applications in everyday life:
- Cooking: Scaling recipes up or down requires dividing or multiplying fractions.
- Sewing: Calculating fabric requirements for a project often involves fraction division.
- Construction: Measuring and cutting materials accurately often needs precise fraction calculations.
- Finance: Understanding percentages and proportions in financial matters relies on fraction manipulation.
Frequently Asked Questions (FAQ)
Q1: Why can't I just divide the numerators and denominators separately?
A1: You can't simply divide the numerators and denominators separately because division by a fraction is fundamentally different from dividing whole numbers. Dividing by a fraction is equivalent to multiplying by its reciprocal, which changes the nature of the operation.
Q2: What if the divisor is a whole number? How does the "keep, change, flip" method apply?
A2: The method still works. A whole number can be expressed as a fraction with a denominator of 1. For example, 4 can be written as 4/1. Applying the method, 4/1 ÷ 2/3 becomes 4/1 × 3/2 = 12/2 = 6.
Q3: Are there other methods to divide fractions?
A3: While the "keep, change, flip" method is the most efficient and widely used, you could also solve fraction division problems by finding a common denominator and then dividing the numerators. However, this method is often more time-consuming.
Q4: What are some common mistakes to avoid when dividing fractions?
A4: Common mistakes include: forgetting to find the reciprocal, incorrectly converting mixed numbers to improper fractions, and making errors in the multiplication step. Carefully following each step of the "keep, change, flip" method will minimize these errors.
Conclusion: Mastering Fraction Division
Dividing by fractions may seem challenging initially, but with a clear understanding of the underlying principles and the efficient "keep, change, flip" method, it becomes a manageable and essential skill. This process is not merely about getting the correct numerical answer (in this case, 6); it's about grasping the conceptual understanding of what it means to divide by a fraction and applying that knowledge to various real-world scenarios. By breaking down the problem step-by-step and visualizing the process, you can confidently tackle any fraction division problem and appreciate the power of this fundamental mathematical operation. Remember, practice is key! The more you work with fractions, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
Is 70 Odd Or Even
Sep 23, 2025
-
How Many Hours Is Full Time
Sep 23, 2025
-
25 18 As A Mixed Number
Sep 23, 2025
-
76 Degrees F To C
Sep 23, 2025
-
1 Gallon How Many Liter
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.