5 1/2 As A Decimal
saludintensiva
Sep 10, 2025 · 5 min read
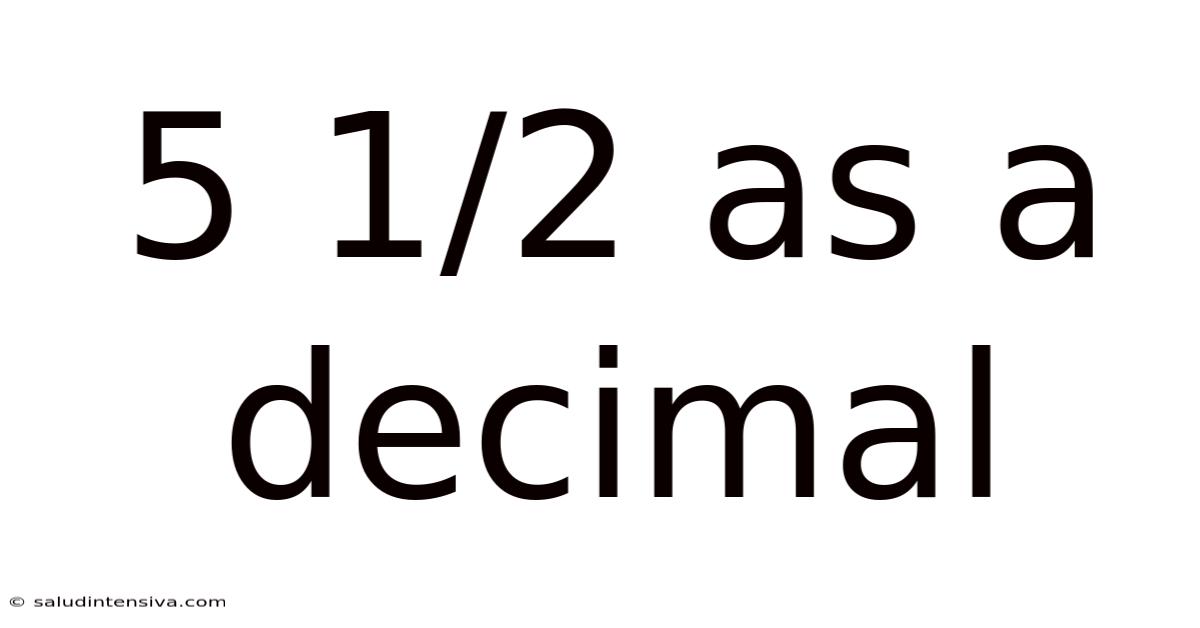
Table of Contents
Understanding 5 1/2 as a Decimal: A Comprehensive Guide
Many of us encounter fractions in our daily lives, whether it's measuring ingredients for a recipe or calculating portions. Converting fractions to decimals is a fundamental skill with applications in various fields, from basic arithmetic to advanced mathematics and computer science. This article will delve deep into understanding how to convert the mixed number 5 1/2 into its decimal equivalent, providing a comprehensive explanation suitable for all levels of mathematical understanding. We'll explore different methods, address common misconceptions, and even touch upon the broader applications of decimal representation. This guide aims to equip you not just with the answer, but with a solid understanding of the underlying principles.
Understanding Mixed Numbers and Decimals
Before we jump into the conversion, let's clarify the terms. A mixed number combines a whole number and a fraction, like 5 1/2. A decimal, on the other hand, represents a number using a base-ten system, where digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, and so on). For example, 5.5 is a decimal representation. The key to converting a mixed number to a decimal is to understand how the fractional part relates to the decimal system.
Method 1: Converting the Fraction to a Decimal
The simplest method for converting 5 1/2 to a decimal involves focusing on the fractional part first. The fraction 1/2 represents one part out of two equal parts of a whole. To express this as a decimal, we perform the division:
1 ÷ 2 = 0.5
This tells us that 1/2 is equivalent to 0.5. Now, we simply add this decimal value to the whole number part of our mixed number:
5 + 0.5 = 5.5
Therefore, 5 1/2 as a decimal is 5.5.
Method 2: Converting the Mixed Number Directly
Alternatively, we can convert the entire mixed number directly to an improper fraction and then divide. To do this, we first convert 5 1/2 into an improper fraction. We multiply the whole number (5) by the denominator of the fraction (2), add the numerator (1), and keep the same denominator (2):
(5 x 2) + 1 = 11
So, 5 1/2 becomes 11/2.
Now, we perform the division:
11 ÷ 2 = 5.5
This again confirms that 5 1/2 as a decimal is 5.5. This method highlights the underlying relationship between fractions and decimals, emphasizing that decimals are simply another way of representing fractions.
Visualizing 5 1/2 as a Decimal
It can be helpful to visualize this conversion. Imagine a number line. The whole numbers are clearly marked (0, 1, 2, 3, 4, 5, etc.). The number 5 1/2 falls exactly halfway between 5 and 6. The decimal system elegantly captures this halfway point by using the digit 5 in the tenths place, representing 5/10, which simplifies to 1/2.
Decimal Place Value and Significance
Understanding decimal place value is crucial. In the decimal 5.5, the digit 5 to the left of the decimal point represents 5 ones (or 5 units). The digit 5 to the right of the decimal point represents 5 tenths (or 5/10). Each place value to the right of the decimal point represents successively smaller fractions of a whole: tenths, hundredths, thousandths, and so on. This system allows us to represent any fractional value using a decimal.
Extending the Concept: Converting Other Mixed Numbers
The methods described above can be applied to convert any mixed number to a decimal. For example, let's consider 3 3/4:
- Method 1 (Fraction First): 3/4 = 0.75; 3 + 0.75 = 3.75
- Method 2 (Improper Fraction): (3 x 4) + 3 = 15; 15/4 = 3.75
Both methods yield the same result: 3 3/4 is equivalent to 3.75. The key is to always divide the numerator by the denominator in the fractional part.
Addressing Common Misconceptions
A common mistake is to simply place the numerator after the decimal point. For example, incorrectly representing 1/2 as 1.2. This is incorrect; the decimal representation requires dividing the numerator by the denominator.
Another misconception involves interpreting the decimal portion independently from the whole number. It's crucial to remember that the decimal part represents a fraction of the whole. The complete decimal representation incorporates both the whole number and the fractional part.
Practical Applications of Decimal Representation
Decimal representation is essential in many real-world scenarios:
- Finance: Money is expressed in decimals (e.g., $5.50).
- Measurement: Metric measurements often utilize decimals (e.g., 5.5 centimeters).
- Science: Scientific calculations frequently involve decimals.
- Computing: Computers rely on binary representation, which can be easily converted to and from decimal.
- Engineering: Precise measurements and calculations in engineering demand the use of decimals.
Frequently Asked Questions (FAQ)
Q: Can all fractions be perfectly represented as terminating decimals?
A: No. Some fractions, when converted to decimals, result in non-terminating, repeating decimals (e.g., 1/3 = 0.333...). These are rational numbers, but their decimal representation doesn't end.
Q: What if the fraction involves larger numbers?
A: The same principles apply. For instance, to convert 127/20 to a decimal, you would simply perform the division: 127 ÷ 20 = 6.35
Q: How can I check if my decimal conversion is correct?
A: You can perform the reverse operation. Convert the decimal back to a fraction and see if you get the original mixed number. For example, 5.5 can be written as 5 + 5/10 = 5 + 1/2 = 5 1/2.
Q: Are there any online tools or calculators to help with these conversions?
A: Yes, many online calculators and websites can perform fraction-to-decimal conversions. These tools can be helpful for checking your work or for handling more complex conversions.
Conclusion
Converting 5 1/2 to a decimal, resulting in 5.5, is a straightforward process that illustrates a fundamental concept in mathematics. Understanding the relationship between fractions and decimals is crucial for proficiency in arithmetic and its applications in various fields. By grasping the different methods and addressing potential misconceptions, you'll be well-equipped to handle similar conversions confidently and accurately. Remember, the core principle is always to divide the numerator by the denominator to obtain the decimal equivalent of a fraction. This knowledge empowers you to navigate numerical calculations with greater ease and understanding. Mastering this concept lays a solid foundation for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
1 2 Divided By 3 4 Fraction
Sep 10, 2025
-
1 5 8 X 2
Sep 10, 2025
-
1 5 As A Percent
Sep 10, 2025
-
Rounding To The Nearest Millionth
Sep 10, 2025
-
Multiples Of 7 To 100
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.