5 12 As A Percent
saludintensiva
Sep 11, 2025 · 5 min read
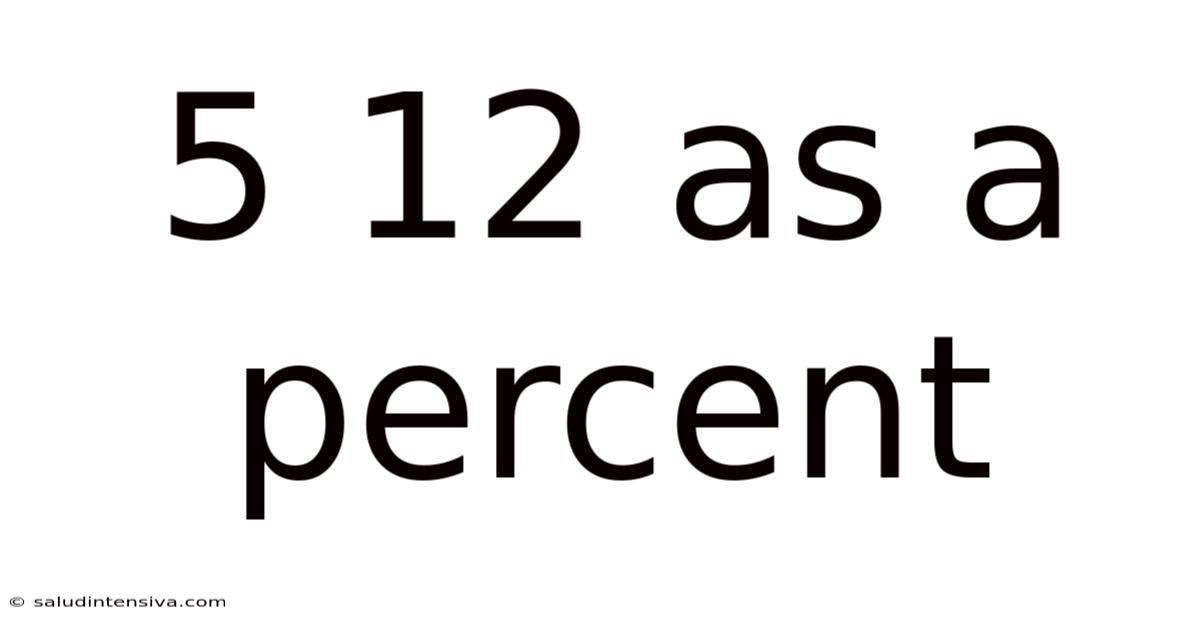
Table of Contents
Understanding 5/12 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from calculating discounts in shopping to understanding financial reports. This article provides a thorough explanation of how to convert the fraction 5/12 into a percentage, along with exploring the underlying concepts and offering practical examples. We'll delve into different methods, ensuring a comprehensive understanding for learners of all levels. By the end, you'll not only know the answer but also grasp the broader principles of percentage calculations.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the specific calculation of 5/12 as a percentage, let's briefly review the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 5/12 means 5 parts out of a total of 12 parts.
-
Decimals: Represent a part of a whole using base-ten notation. Decimals are essentially fractions where the denominator is a power of 10 (e.g., 10, 100, 1000).
-
Percentages: Express a part of a whole as a fraction of 100. The symbol "%" signifies "per hundred." Therefore, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
These three forms are interchangeable, meaning you can convert one into another. Understanding this interrelationship is crucial for solving percentage problems.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most straightforward method for converting 5/12 to a percentage. It involves two steps:
Step 1: Convert the fraction to a decimal.
To do this, we divide the numerator (5) by the denominator (12):
5 ÷ 12 ≈ 0.416666...
Notice that the result is a repeating decimal. For practical purposes, we'll round this to a reasonable number of decimal places. Using four decimal places, we get 0.4167.
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.4167 × 100 = 41.67%
Therefore, 5/12 is approximately 41.67%. The "..." in the decimal representation indicates that the digits "6" repeat infinitely. The level of rounding depends on the required accuracy; for most applications, two or three decimal places are sufficient.
Method 2: Using Proportions to Solve for the Percentage
This method uses the concept of proportions to directly find the percentage equivalent. We set up a proportion where one ratio represents the fraction (5/12) and the other ratio represents the percentage (x/100), where 'x' is the unknown percentage we want to find.
The proportion is set up as follows:
5/12 = x/100
To solve for 'x', we cross-multiply:
12x = 500
Now, we divide both sides by 12:
x = 500/12 ≈ 41.67
Therefore, x ≈ 41.67%, confirming the result from Method 1. This method highlights the underlying proportional relationship between fractions and percentages.
Method 3: Understanding the Concept Through Visual Representation
Visual aids can significantly enhance understanding. Imagine a pizza cut into 12 equal slices. If you take 5 slices, you have 5/12 of the pizza. To represent this as a percentage, we need to figure out what proportion of a 100-slice pizza (representing 100%) would be equivalent to 5 slices out of 12.
This visual approach helps solidify the connection between the fraction and its percentage equivalent, although it's less practical for complex fractions.
Detailed Explanation of the Calculation: Addressing Potential Confusion
The core of the calculation lies in understanding that a percentage is a fraction with a denominator of 100. When we divide 5 by 12, we're finding the decimal equivalent of the fraction. Multiplying by 100 then scales this decimal to represent the fraction as parts of 100, which is the definition of a percentage.
The repeating decimal (0.416666...) arises because 12 is not a factor of 100. This means the fraction 5/12 cannot be expressed as a simple, terminating decimal. Rounding is necessary for practical use, but it's important to acknowledge the inherent inexactness introduced by rounding.
Practical Applications: Where Percentage Conversions Matter
The ability to convert fractions to percentages is invaluable in numerous real-world scenarios:
-
Finance: Calculating interest rates, loan repayments, discounts, and profit margins.
-
Retail: Determining sale prices, calculating markups, and understanding profit percentages.
-
Science: Expressing experimental results, analyzing data, and presenting findings.
-
Everyday Life: Calculating tips, sharing expenses, understanding statistics presented in percentages.
Frequently Asked Questions (FAQ)
Q: Why do we multiply by 100 when converting a decimal to a percentage?
A: Multiplying by 100 is equivalent to expressing the decimal as a fraction with a denominator of 100, which is the fundamental definition of a percentage.
Q: What if I need a more precise answer than 41.67%?
A: You can use more decimal places in your calculation. The more decimal places you use, the more accurate your percentage will be. However, for most practical purposes, two or three decimal places provide sufficient accuracy.
Q: Are there other ways to convert 5/12 to a percentage?
A: While the methods outlined above are the most common and straightforward, more advanced techniques involving continued fractions or infinite series could provide a more precise answer, although they are considerably more complex.
Q: Can I use a calculator to do this conversion?
A: Yes, most calculators can perform this calculation directly. Simply enter 5 ÷ 12 and then multiply the result by 100.
Conclusion: Mastering Percentage Conversions
Converting 5/12 to a percentage, resulting in approximately 41.67%, demonstrates a fundamental mathematical skill applicable across numerous fields. Understanding the underlying principles, as explained through different methods and visual representations, allows for a deeper grasp of the concept and its practical implications. The ability to seamlessly convert between fractions, decimals, and percentages is a valuable tool for problem-solving in both academic and real-world contexts. Remember to always consider the required level of accuracy when rounding decimal values. By mastering this skill, you enhance your numerical literacy and ability to confidently navigate various quantitative tasks.
Latest Posts
Latest Posts
-
What Is A 1 5 Ratio
Sep 12, 2025
-
Equivalent Fraction Of 8 20
Sep 12, 2025
-
2 3 10 As A Decimal
Sep 12, 2025
-
6 Ft By 3 Ft
Sep 12, 2025
-
3 To The 7 Power
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 5 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.