2 3/10 As A Decimal
saludintensiva
Sep 12, 2025 · 6 min read
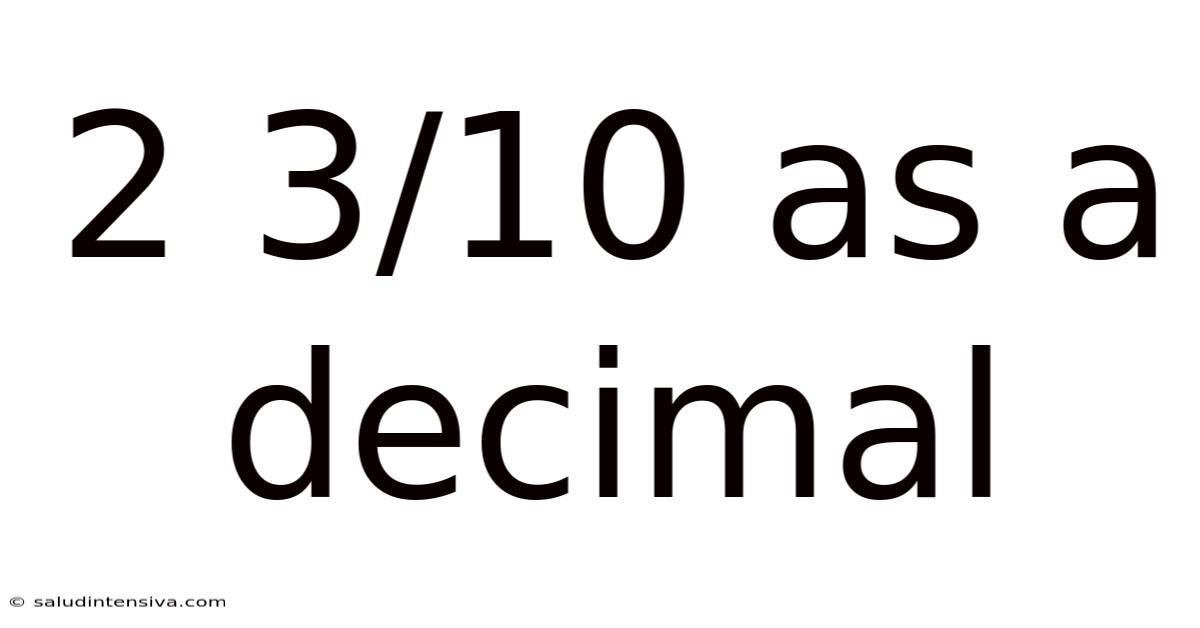
Table of Contents
2 3/10 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 2 3/10 into its decimal equivalent, providing a detailed explanation and exploring related concepts. We'll cover the process step-by-step, explain the underlying principles, and even delve into some frequently asked questions. By the end, you'll not only know the answer but also understand the why behind the conversion. This knowledge is crucial for various applications, from basic arithmetic to more advanced mathematical concepts.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion, let's refresh our understanding of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 2 3/10. This means we have two whole units and three-tenths of another unit. A decimal, on the other hand, represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part. For example, 2.3 is a decimal number where 2 is the whole number and .3 represents three-tenths.
Converting 2 3/10 to a Decimal: A Step-by-Step Approach
The conversion of 2 3/10 to a decimal is relatively straightforward. We can break it down into these simple steps:
-
Separate the Whole Number: The first step involves separating the whole number part (2) from the fractional part (3/10). We'll deal with each part separately.
-
Convert the Fraction to a Decimal: The fraction 3/10 represents three parts out of ten equal parts. Since the denominator is a power of 10 (10¹), the conversion is particularly easy. To convert a fraction to a decimal, you divide the numerator (the top number) by the denominator (the bottom number). In this case:
3 ÷ 10 = 0.3
-
Combine the Whole Number and Decimal: Now, we simply combine the whole number we separated earlier (2) with the decimal equivalent of the fraction (0.3). This gives us the final answer:
2 + 0.3 = 2.3
Therefore, 2 3/10 as a decimal is 2.3.
A Deeper Dive: Understanding the Principles
The method above provides a practical approach, but understanding the underlying principles strengthens your mathematical foundation. The decimal system is based on powers of 10. Each place value to the right of the decimal point represents a decreasing power of 10:
- Tenths (1/10): The first place to the right of the decimal point represents tenths.
- Hundredths (1/100): The second place represents hundredths.
- Thousandths (1/1000): The third place represents thousandths, and so on.
In our example, 3/10 directly translates to 0.3 because the 3 occupies the tenths place.
Converting Other Fractions to Decimals
While 2 3/10 is a simple example, the principles can be applied to other fractions. However, if the denominator isn't a power of 10 (like 10, 100, 1000, etc.), you'll need to perform long division to obtain the decimal equivalent.
For example, let's consider the fraction 1/4:
- Divide the numerator by the denominator: 1 ÷ 4 = 0.25
Therefore, 1/4 as a decimal is 0.25.
Similarly, for a fraction like 2/3, the division results in a repeating decimal (0.666...). This means the decimal representation goes on infinitely, repeating the digit 6. We often round these repeating decimals to a certain number of decimal places for practical purposes.
Working with Mixed Numbers: A General Approach
The process of converting a mixed number to a decimal involves the same steps as shown with 2 3/10. You always separate the whole number and convert the fraction to its decimal equivalent. Let's look at another example: 5 7/20.
-
Separate the Whole Number: The whole number is 5.
-
Convert the Fraction to a Decimal: 7/20 = 0.35 (7 ÷ 20 = 0.35)
-
Combine: 5 + 0.35 = 5.35
Therefore, 5 7/20 as a decimal is 5.35.
As you can see, regardless of the fraction's complexity, the approach remains consistent. The key is to understand the relationship between fractions and decimals, which is fundamentally about representing parts of a whole.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is vital in many real-world scenarios. Some examples include:
-
Financial Calculations: Dealing with monetary values often involves fractions of a dollar (cents). Converting fractions to decimals is essential for accurate calculations.
-
Measurements: Many measurement systems use decimal notation. Converting fractional measurements to decimal form simplifies calculations and comparisons.
-
Scientific Calculations: Science and engineering often involve precise measurements and calculations. Decimal representation improves accuracy and eases computation.
-
Data Analysis: In data analysis and statistics, decimal representation of data is common for statistical calculations and interpretations.
-
Computer Programming: Computers use binary systems (base-2), but many programming languages readily handle decimal numbers, making conversions necessary.
Frequently Asked Questions (FAQ)
Q1: What if the fraction has a large denominator?
A1: If the denominator is not a power of 10, you'll need to perform long division to convert the fraction to a decimal. This may result in a terminating decimal (like 0.25) or a repeating decimal (like 0.666...). For repeating decimals, you can round off to a specific number of decimal places based on the required accuracy.
Q2: Can I use a calculator to convert fractions to decimals?
A2: Yes, most calculators have the capability to perform this conversion directly. Simply enter the fraction (either as a mixed number or an improper fraction) and the calculator will provide the decimal equivalent.
Q3: Why is understanding decimal conversion important?
A3: Understanding decimal conversion is crucial for various applications, ranging from everyday calculations to advanced mathematical and scientific fields. It's a fundamental concept that enhances your ability to solve problems involving fractions and decimals accurately and efficiently. It also improves your number sense and mathematical reasoning skills.
Q4: What if the fraction is an improper fraction?
A4: An improper fraction (where the numerator is larger than the denominator) should first be converted into a mixed number before converting it into a decimal. For example, 17/10 can be rewritten as 1 7/10, then converted to 1.7.
Q5: Are there any shortcuts for converting fractions with denominators that are factors of 100 or 1000?
A5: Yes! If the denominator can be easily multiplied to become 10, 100, or 1000, then you can adjust the numerator accordingly to directly obtain the decimal representation. For example, 3/25 = 12/100 = 0.12.
Conclusion
Converting fractions like 2 3/10 to their decimal equivalents is a fundamental mathematical skill with broad practical applications. This guide has provided a step-by-step approach, explored the underlying principles, and addressed frequently asked questions. By mastering this skill, you'll enhance your overall mathematical proficiency and confidently tackle various problems involving fractions and decimals in any context. Remember, practice makes perfect – the more you work with these conversions, the more intuitive they will become. Understanding the why behind the conversion, not just the how, will ultimately solidify your grasp of this essential mathematical concept.
Latest Posts
Latest Posts
-
2 Out Of 12 Percentage
Sep 12, 2025
-
9 5 Percent As A Decimal
Sep 12, 2025
-
59 Degrees F To C
Sep 12, 2025
-
12 15 In The Simplest Form
Sep 12, 2025
-
Order Doesnt Matter With Replacement
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 2 3/10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.