9.5 Percent As A Decimal
saludintensiva
Sep 12, 2025 · 6 min read
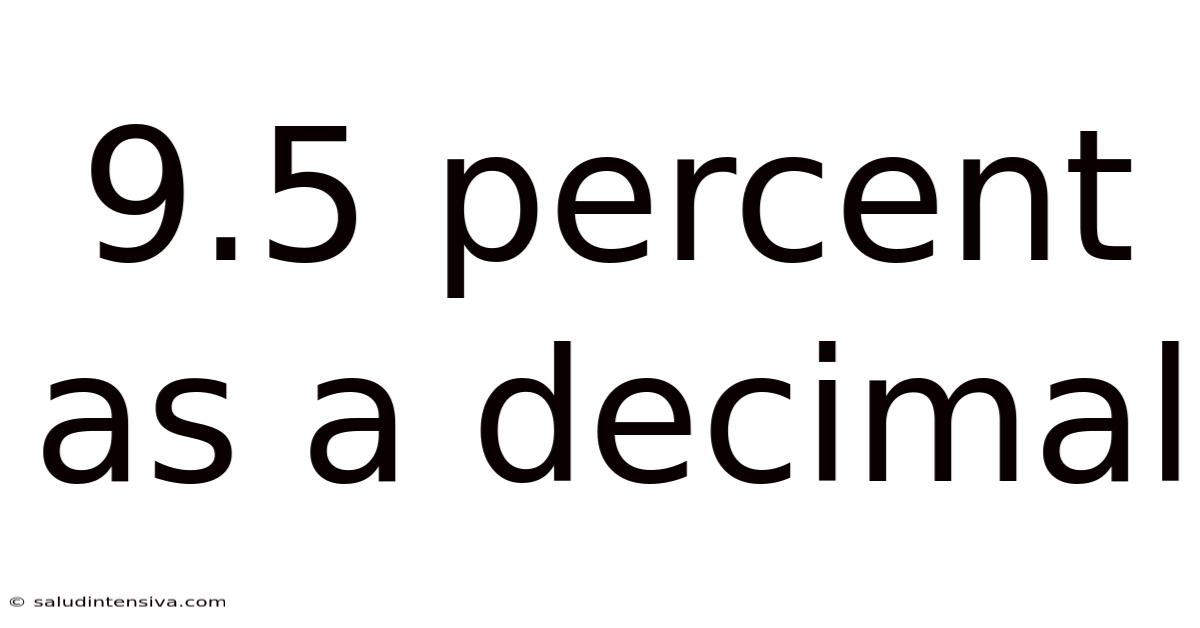
Table of Contents
9.5 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics, crucial for various applications in everyday life, finance, science, and more. This article delves deep into converting 9.5 percent to its decimal form, explaining the process step-by-step and providing a broader context for working with percentages and decimals. We'll explore the underlying principles, practical examples, and even touch upon some common misconceptions. By the end, you'll not only know the decimal equivalent of 9.5% but also possess a solid understanding of percentage-to-decimal conversions.
Understanding Percentages and Decimals
Before diving into the conversion of 9.5%, let's refresh our understanding of percentages and decimals. A percentage represents a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 9.5% means 9.5 out of 100.
A decimal, on the other hand, is a way of expressing a number using base-10. The digits to the right of the decimal point represent fractions of powers of 10 (tenths, hundredths, thousandths, and so on). For instance, 0.5 represents five-tenths (5/10), and 0.05 represents five-hundredths (5/100).
Converting 9.5 Percent to a Decimal: The Method
The conversion of a percentage to a decimal is straightforward. The key is to remember that a percentage is simply a fraction with a denominator of 100. To convert a percentage to a decimal, we divide the percentage by 100. This is equivalent to moving the decimal point two places to the left.
Let's apply this to 9.5%:
-
Write the percentage as a fraction: 9.5% can be written as 9.5/100.
-
Perform the division: Dividing 9.5 by 100 gives us 0.095.
-
Alternatively, move the decimal point: Starting with 9.5%, move the decimal point two places to the left. This yields 0.095.
Therefore, 9.5% as a decimal is 0.095.
Practical Applications of 9.5% and its Decimal Equivalent
The decimal equivalent of 9.5% finds numerous applications across various fields:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins often involves converting percentages to decimals. For example, if a bank offers a 9.5% annual interest rate on a savings account, this translates to a decimal rate of 0.095 for calculations.
-
Science: In scientific research, percentages and decimals are frequently used to represent proportions, experimental results, and statistical data. A 9.5% increase in a certain variable, for instance, would be represented as 0.095 in calculations or graphs.
-
Everyday Life: From calculating tips in restaurants (a 9.5% tip on a bill), to understanding sales discounts (a 9.5% off sale), the conversion between percentages and decimals is frequently used in our daily lives.
-
Statistics: Percentages and decimals are fundamental in statistical analysis. Representing data as proportions, calculating probabilities, and interpreting statistical results all rely on a clear understanding of these concepts.
Working with Percentages Greater than 100%
While the previous examples focused on percentages less than 100%, it's important to understand how to handle percentages exceeding 100%. These percentages represent values greater than the whole (100%).
For instance, if we have 125%, the conversion to decimal follows the same principle:
-
Write as a fraction: 125/100
-
Perform the division: 125 ÷ 100 = 1.25
-
Move the decimal point: Moving the decimal point two places to the left in 125.0% gives 1.25.
Therefore, 125% as a decimal is 1.25. Notice that the decimal value is greater than 1, reflecting the fact that it represents a value larger than the whole.
Common Misconceptions Regarding Percentage-Decimal Conversions
Several common misconceptions can lead to errors in percentage-to-decimal conversions:
-
Forgetting to divide by 100: Some individuals might mistakenly think that 9.5% is simply 0.95. Remember, the crucial step is to divide by 100 (or move the decimal point two places to the left).
-
Incorrect decimal placement: Confusion about the placement of the decimal point is another frequent error. Ensure you move the decimal point two places to the left, not right, when converting from a percentage to a decimal.
-
Misinterpreting percentages greater than 100%: It's important to understand that percentages larger than 100% represent values greater than the whole. This means their decimal equivalents will be greater than 1.
Further Exploration: Converting Decimals to Percentages
The reverse process – converting decimals to percentages – is equally important. To do this, we multiply the decimal by 100 and add the percent symbol (%).
For example, converting 0.095 back to a percentage:
-
Multiply by 100: 0.095 x 100 = 9.5
-
Add the percent symbol: 9.5%
This reinforces the inverse relationship between percentages and decimals.
Real-World Examples and Exercises
Let's solidify our understanding with a few practical examples:
Example 1: A store offers a 9.5% discount on all items. If an item costs $50, what is the discount amount?
- Solution: Convert 9.5% to a decimal (0.095). Then multiply this by the original price: 0.095 x $50 = $4.75. The discount is $4.75.
Example 2: A student scored 85 out of 100 on a test. What is their percentage score?
- Solution: First, calculate the fraction: 85/100. Then convert this fraction to a percentage (85%). Convert to a decimal (0.85).
Example 3: The population of a town increased by 0.125. What is the percentage increase?
- Solution: Multiply the decimal increase by 100: 0.125 x 100 = 12.5%. The population increased by 12.5%.
Frequently Asked Questions (FAQ)
Q1: Can I convert percentages with fractions directly to decimals?
A1: Yes, you can. For example, 12 1/2% (or 12.5%) can be converted to a decimal by dividing 12.5 by 100, which gives 0.125.
Q2: What if I have a percentage like 0.5%?
A2: Treat this the same way. Divide 0.5 by 100, which equals 0.005.
Q3: Why is it important to understand percentage-to-decimal conversions?
A3: This conversion is vital for accurate calculations in finance, science, statistics, and numerous everyday situations. Understanding this process is essential for various mathematical applications.
Q4: Are there any online tools to help with these conversions?
A4: While this article provides a comprehensive method, several online calculators can perform percentage-to-decimal conversions for verification or quick calculations.
Conclusion
Converting 9.5% to its decimal equivalent (0.095) is a simple yet crucial skill. Mastering this conversion, along with the broader concepts of percentages and decimals, empowers you to tackle various mathematical problems effectively across diverse fields. Remember the fundamental steps: divide the percentage by 100 or move the decimal point two places to the left. Understanding this process not only helps you solve specific problems but also builds a strong foundation for more advanced mathematical concepts. Through practical application and a clear understanding of the underlying principles, you can confidently navigate the world of percentages and decimals.
Latest Posts
Latest Posts
-
Fraction Equivalent To 2 4
Sep 12, 2025
-
1930 Military Time To Normal
Sep 12, 2025
-
Number To Words Indian Currency
Sep 12, 2025
-
12 Out Of 15 Percent
Sep 12, 2025
-
Convert 25 F To C
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 9.5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.