5 14 As A Percent
saludintensiva
Sep 13, 2025 · 5 min read
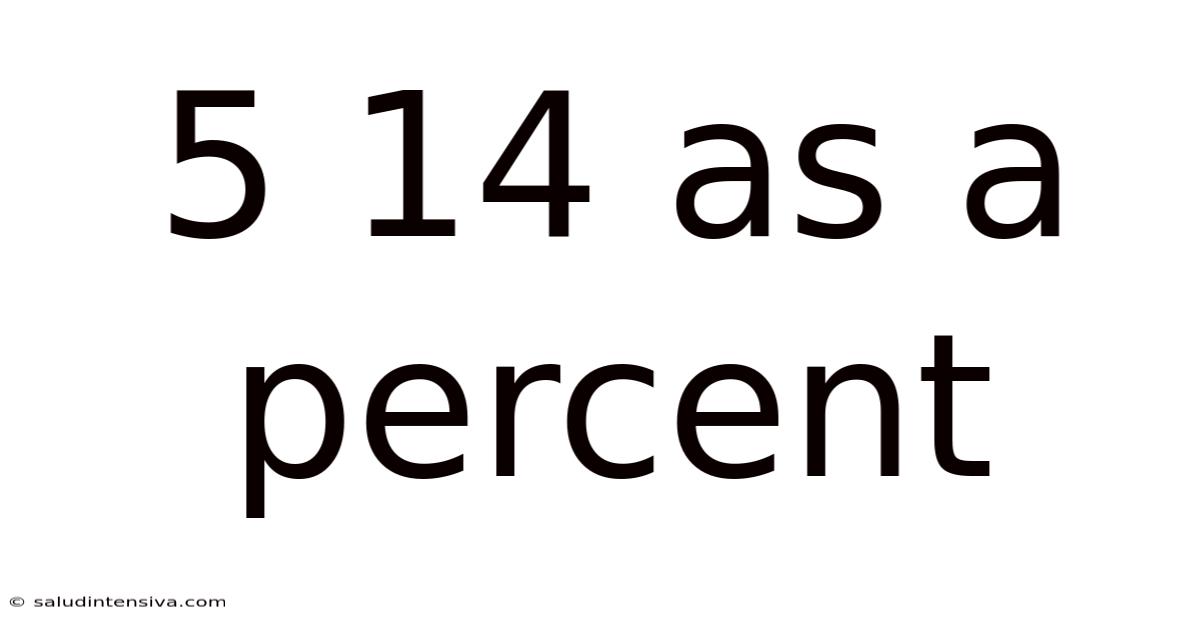
Table of Contents
Decoding 5/14 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and tax to understanding statistics and financial data. This article will delve into the process of converting the fraction 5/14 into a percentage, exploring different methods, providing detailed explanations, and addressing common questions. We'll cover the underlying mathematical principles, practical applications, and even touch upon the broader context of fraction-to-percentage conversions. By the end, you'll not only know the answer but also grasp the underlying mechanics and be able to confidently tackle similar problems.
Understanding Fractions and Percentages
Before diving into the conversion of 5/14, let's establish a solid foundation. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). In the fraction 5/14, 5 is the numerator and 14 is the denominator. This means we are considering 5 parts out of a total of 14 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100 parts. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. The key to converting fractions to percentages is to find the equivalent fraction with a denominator of 100.
Method 1: Direct Conversion using Division
The most straightforward method to convert 5/14 into a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (5) by the denominator (14). Using a calculator or long division, we get: 5 ÷ 14 ≈ 0.3571
-
Convert the decimal to a percentage: Multiply the decimal result by 100. This shifts the decimal point two places to the right. Therefore: 0.3571 × 100 ≈ 35.71%
Therefore, 5/14 is approximately equal to 35.71%. The approximation arises because the decimal representation of 5/14 is a non-terminating decimal; it continues infinitely. For practical purposes, rounding to two decimal places (35.71%) is usually sufficient.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
While the division method is efficient, understanding the principle of equivalent fractions provides a deeper insight. The goal is to find a fraction equivalent to 5/14 but with a denominator of 100. This can be achieved through the following steps:
-
Set up a proportion: We want to find a number 'x' such that 5/14 = x/100.
-
Cross-multiply: This gives us the equation: 14x = 500
-
Solve for x: Divide both sides by 14: x = 500/14 ≈ 35.71
Therefore, 5/14 is approximately equivalent to 35.71/100, which is 35.71%. This method reinforces the concept of equivalent fractions and the underlying logic of percentage conversions.
Method 3: Using Proportions and Ratio
We can also approach this problem from a ratio and proportion perspective. The fraction 5/14 represents a ratio of 5 to 14. To express this as a percentage, we need to find the equivalent ratio where the second term is 100. We can set up the proportion:
5/14 = x/100
Cross-multiplying gives us: 14x = 500
Solving for x: x = 500/14 ≈ 35.71
This confirms that 5/14 is approximately 35.71%. This approach highlights the versatility of ratios and proportions in solving percentage problems.
Illustrative Example: Practical Application
Let's consider a real-world scenario. Suppose you're a teacher grading student assignments. Out of 14 students, 5 students scored above 90%. To calculate the percentage of students who scored above 90%, you would use the fraction 5/14. Following the methods outlined above, you'd find that approximately 35.71% of students achieved a score above 90%. This information is crucial for assessing overall class performance and identifying areas needing attention.
Further Exploration: Recurring Decimals and Precision
It's important to acknowledge that the decimal representation of 5/14 (0.357142857142...) is a recurring decimal. This means the digits 3571428 repeat infinitely. Our calculations have involved rounding to two decimal places for practical purposes. However, depending on the context, higher precision might be necessary. For instance, in scientific or financial calculations, more decimal places might be required to ensure accuracy. Understanding the limitations of rounding and the nature of recurring decimals is crucial for interpreting results correctly.
Frequently Asked Questions (FAQ)
Q1: Is there a way to express 5/14 as an exact percentage without rounding?
A1: No, there isn't. Because the decimal equivalent of 5/14 is a recurring decimal, it cannot be expressed as an exact percentage without using the fractional representation itself (5/14) or resorting to an infinitely long decimal representation. Rounding is necessary for practical use.
Q2: How can I perform these calculations without a calculator?
A2: You can use long division to convert the fraction to a decimal. Long division is a fundamental arithmetic skill that allows you to manually divide the numerator by the denominator. While it might be more time-consuming than using a calculator, it provides a deeper understanding of the process.
Q3: What are some other common applications of converting fractions to percentages?
A3: Converting fractions to percentages is widely used in many areas, including:
- Finance: Calculating interest rates, discounts, and profit margins.
- Statistics: Representing data in a more easily understandable format.
- Science: Expressing experimental results and probabilities.
- Everyday life: Determining tips, sales tax, and portion sizes.
Q4: Are there online tools or calculators that can perform this conversion?
A4: Yes, numerous online calculators are readily available to perform fraction-to-percentage conversions. These tools can be particularly helpful for complex fractions or when dealing with larger numbers. (Note: As per the instructions, I cannot provide links to external websites).
Conclusion
Converting 5/14 to a percentage, approximately 35.71%, involves a straightforward process that can be tackled through different methods. Understanding these methods, whether through direct division, finding equivalent fractions, or utilizing ratios and proportions, provides a comprehensive grasp of the underlying mathematical principles. This skill is invaluable across various disciplines and daily life applications, highlighting the importance of mastering fraction-to-percentage conversions. Remember to consider the level of precision needed based on the specific context, and don't hesitate to utilize tools like long division or online calculators to aid in your calculations. The ability to confidently convert fractions to percentages is a testament to a strong mathematical foundation and a valuable skill to possess.
Latest Posts
Latest Posts
-
18 Deg C To F
Sep 13, 2025
-
2 3 5 9 Simplify
Sep 13, 2025
-
How Long Is 162 Minutes
Sep 13, 2025
-
When Was 21 Weeks Ago
Sep 13, 2025
-
3 1 5 As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 14 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.