5 2 As A Percentage
saludintensiva
Sep 16, 2025 · 6 min read
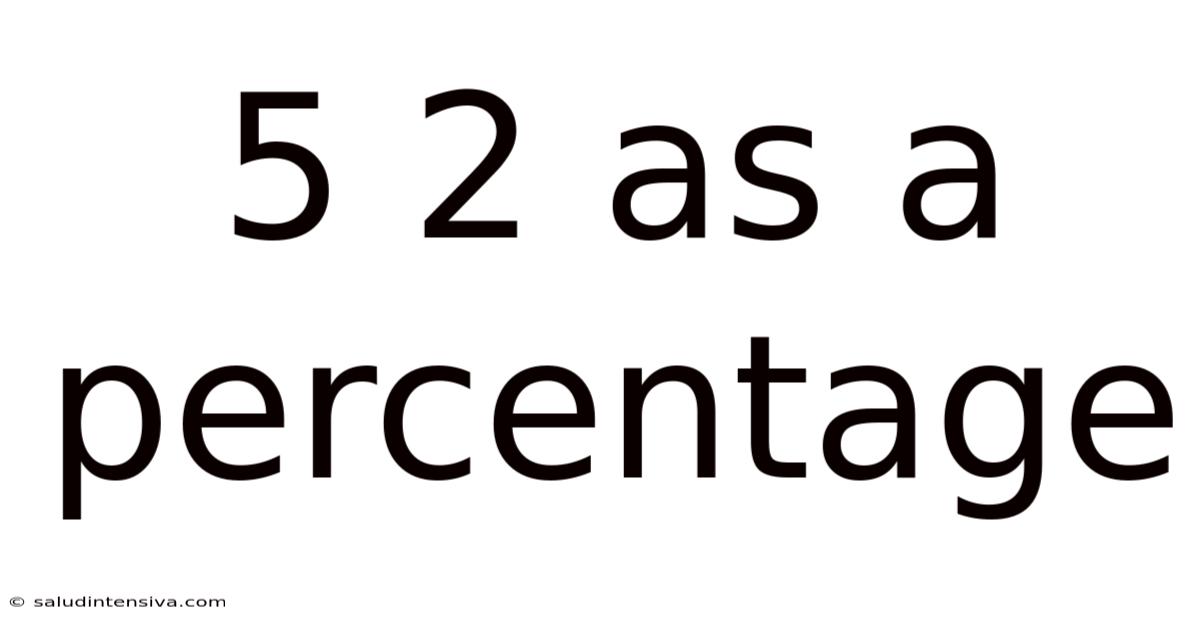
Table of Contents
Decoding 5/2 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, crucial for various applications in daily life, from calculating discounts to understanding financial reports. This article will delve deep into converting the fraction 5/2 into a percentage, exploring the underlying concepts and providing practical examples. We'll also address common misconceptions and answer frequently asked questions to ensure a complete understanding of this seemingly simple yet important mathematical concept. This guide will equip you with the knowledge and confidence to tackle similar fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before we dive into converting 5/2 into a percentage, let's solidify our understanding of the fundamental concepts involved. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
A percentage, on the other hand, represents a fraction out of 100. The term "percent" literally means "out of one hundred" (from the Latin "per centum"). Therefore, a percentage expresses a proportion relative to 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 5/2 to a Percentage: The Step-by-Step Process
The conversion of 5/2 to a percentage involves two main steps:
-
Convert the fraction to a decimal: To convert a fraction to a decimal, we divide the numerator by the denominator. In this case, we divide 5 by 2:
5 ÷ 2 = 2.5
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. In this case:
2.5 × 100 = 250
Therefore, 5/2 as a percentage is 250%.
Why is the Percentage Greater than 100%?
It's important to note that the resulting percentage, 250%, is greater than 100%. This is because the fraction 5/2 is an improper fraction, meaning the numerator (5) is larger than the denominator (2). Improper fractions represent values greater than one whole. When we convert an improper fraction to a percentage, we naturally obtain a percentage greater than 100%. This simply indicates that the fraction represents more than one whole.
Illustrative Examples
Let's consider some real-world scenarios where understanding this conversion is helpful:
-
Profit Margin: Imagine a business that invested $2 and made a profit of $5. Their profit margin would be 5/2 = 2.5, or 250%. This means they made a profit of 250% of their initial investment.
-
Price Increase: If the price of an item increased from $2 to $5, the percentage increase is calculated as (5-2)/2 * 100% = 150%. While this is a different calculation (percentage change), understanding the 250% representation helps contextualize the magnitude of the price increase relative to the original price.
-
Exam Scores: While less likely in a typical exam scoring system, if a student's score is expressed as 5 out of 2 possible points (perhaps due to extra credit or bonus marks), this would represent a score of 250%.
Addressing Common Misconceptions
A common mistake when converting fractions to percentages is forgetting to multiply by 100 in the final step. Remember, a percentage is always expressed as a value out of 100. Another common error arises when dealing with improper fractions – students may struggle to interpret a percentage greater than 100%. It's crucial to remember that percentages exceeding 100% are perfectly valid and represent values greater than one whole.
The Mathematical Explanation: Proportions and Ratios
The conversion of fractions to percentages relies on the fundamental concept of proportions and ratios. A ratio is a comparison between two numbers, while a proportion is a statement that two ratios are equal. When we convert 5/2 to a percentage, we are essentially setting up a proportion:
5/2 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
5 * 100 = 2 * x
500 = 2x
x = 500/2 = 250
This demonstrates the mathematical basis underlying the conversion process.
Practical Applications in Different Fields
The ability to convert fractions to percentages finds application across various disciplines:
-
Finance: Calculating interest rates, profit margins, and returns on investment.
-
Statistics: Representing data and probabilities as percentages for easier interpretation.
-
Science: Expressing experimental results and measurement errors as percentages.
-
Everyday Life: Calculating discounts, sales tax, and tips.
Advanced Concepts: Decimal Places and Rounding
In some cases, the decimal representation of a fraction may have an infinite number of decimal places. For example, converting 1/3 to a decimal yields 0.3333... When converting such decimals to percentages, you may need to round the result to a specific number of decimal places to achieve practicality. The level of rounding depends on the context and required accuracy. For example, 0.3333... rounded to two decimal places is 0.33, which translates to 33%.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted into percentages?
A1: Yes, all fractions, whether proper or improper, can be converted into percentages by following the steps outlined above.
Q2: What if the denominator of the fraction is zero?
A2: Division by zero is undefined in mathematics. Therefore, a fraction with a denominator of zero cannot be converted to a percentage.
Q3: How do I convert a mixed number (e.g., 2 1/2) to a percentage?
A3: First, convert the mixed number into an improper fraction. In this example, 2 1/2 becomes 5/2. Then, follow the steps to convert the improper fraction to a percentage, as explained earlier. The result would be 250%.
Q4: What is the difference between a percentage increase and a percentage expressed as a fraction?
A4: A percentage increase calculates the change relative to an initial value. In contrast, expressing a fraction as a percentage directly represents the fraction's value relative to 100, regardless of any change or initial value.
Q5: Are there any online calculators that can perform this conversion?
A5: Yes, many online calculators are available that can convert fractions to percentages. However, understanding the underlying process is crucial for developing mathematical proficiency.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill with widespread applications. While the process itself is relatively straightforward, a solid grasp of the underlying concepts—fractions, decimals, percentages, proportions, and ratios—is essential for accurate and confident conversions. This comprehensive guide has provided a step-by-step process, illustrated examples, addressed common misconceptions, and answered frequently asked questions to ensure a thorough understanding of converting 5/2 (and other fractions) into a percentage. Remember, practice is key to mastering this crucial mathematical skill. By consistently applying these methods, you'll confidently navigate the world of fractions and percentages, whether you're calculating discounts at the store or analyzing financial data.
Latest Posts
Latest Posts
-
Two Equivalent Fractions Of 3 4
Sep 16, 2025
-
What Is Half Of 47
Sep 16, 2025
-
What Percentage Is 2 5
Sep 16, 2025
-
2 To The 11 Power
Sep 16, 2025
-
6 38 24 Hour Time
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 5 2 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.